COCO Denoiser: Using Co-Coercivity for Variance Reduction in Stochastic Convex Optimization

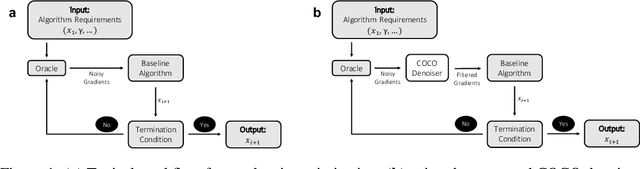
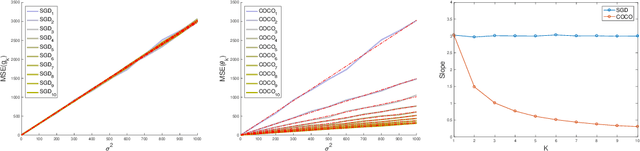
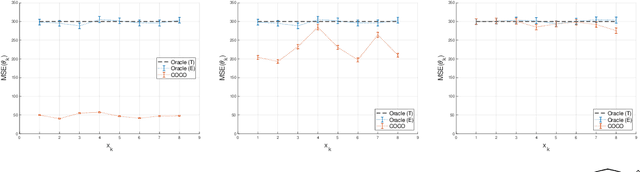
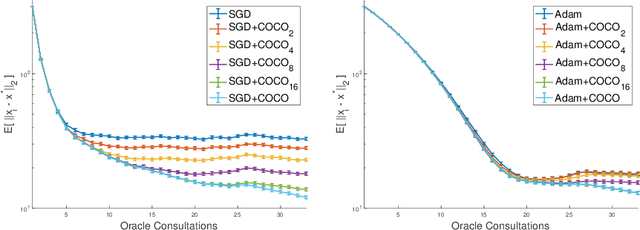
First-order methods for stochastic optimization have undeniable relevance, in part due to their pivotal role in machine learning. Variance reduction for these algorithms has become an important research topic. In contrast to common approaches, which rarely leverage global models of the objective function, we exploit convexity and L-smoothness to improve the noisy estimates outputted by the stochastic gradient oracle. Our method, named COCO denoiser, is the joint maximum likelihood estimator of multiple function gradients from their noisy observations, subject to co-coercivity constraints between them. The resulting estimate is the solution of a convex Quadratically Constrained Quadratic Problem. Although this problem is expensive to solve by interior point methods, we exploit its structure to apply an accelerated first-order algorithm, the Fast Dual Proximal Gradient method. Besides analytically characterizing the proposed estimator, we show empirically that increasing the number and proximity of the queried points leads to better gradient estimates. We also apply COCO in stochastic settings by plugging it in existing algorithms, such as SGD, Adam or STRSAGA, outperforming their vanilla versions, even in scenarios where our modelling assumptions are mismatched.

Sparse Continuous Distributions and Fenchel-Young Losses

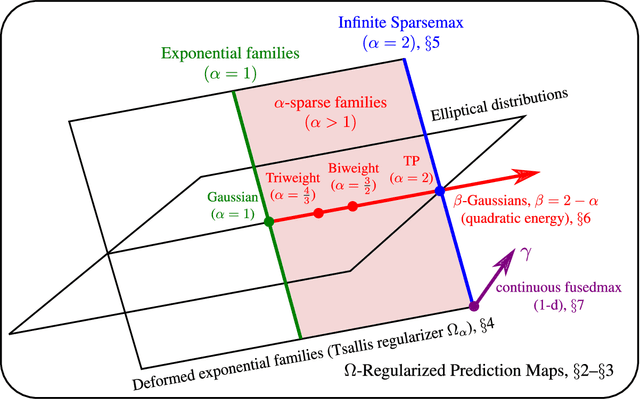
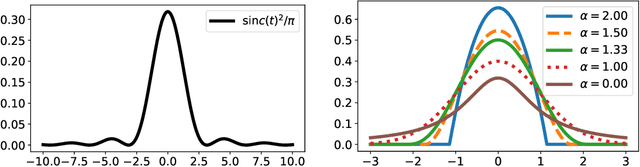
Exponential families are widely used in machine learning; they include many distributions in continuous and discrete domains (e.g., Gaussian, Dirichlet, Poisson, and categorical distributions via the softmax transformation). Distributions in each of these families have fixed support. In contrast, for finite domains, there has been recent works on sparse alternatives to softmax (e.g. sparsemax, $\alpha$-entmax, and fusedmax) and corresponding losses, which have varying support. This paper expands that line of work in several directions: first, it extends $\Omega$-regularized prediction maps and Fenchel-Young losses to arbitrary domains (possibly countably infinite or continuous). For linearly parametrized families, we show that minimization of Fenchel-Young losses is equivalent to moment matching of the statistics, generalizing a fundamental property of exponential families. When $\Omega$ is a Tsallis negentropy with parameter $\alpha$, we obtain "deformed exponential families," which include $\alpha$-entmax and sparsemax ($\alpha$ = 2) as particular cases. For quadratic energy functions in continuous domains, the resulting densities are $\beta$-Gaussians, an instance of elliptical distributions that contain as particular cases the Gaussian, biweight, triweight and Epanechnikov densities, and for which we derive closed-form expressions for the variance, Tsallis entropy, and Fenchel-Young loss. When $\Omega$ is a total variation or Sobolev regularizer, we obtain a continuous version of the fusedmax. Finally, we introduce continuous-domain attention mechanisms, deriving efficient gradient backpropagation algorithms for $\alpha \in \{1, 4/3, 3/2, 2\}$. Using them, we demonstrate our sparse continuous distributions for attention-based audio classification and visual question answering, showing that they allow attending to time intervals and compact regions.

Multimodal Continuous Visual Attention Mechanisms

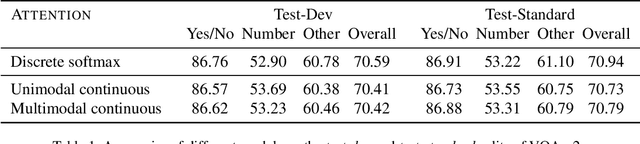
Visual attention mechanisms are a key component of neural network models for computer vision. By focusing on a discrete set of objects or image regions, these mechanisms identify the most relevant features and use them to build more powerful representations. Recently, continuous-domain alternatives to discrete attention models have been proposed, which exploit the continuity of images. These approaches model attention as simple unimodal densities (e.g. a Gaussian), making them less suitable to deal with images whose region of interest has a complex shape or is composed of multiple non-contiguous patches. In this paper, we introduce a new continuous attention mechanism that produces multimodal densities, in the form of mixtures of Gaussians. We use the EM algorithm to obtain a clustering of relevant regions in the image, and a description length penalty to select the number of components in the mixture. Our densities decompose as a linear combination of unimodal attention mechanisms, enabling closed-form Jacobians for the backpropagation step. Experiments on visual question answering in the VQA-v2 dataset show competitive accuracies and a selection of regions that mimics human attention more closely in VQA-HAT. We present several examples that suggest how multimodal attention maps are naturally more interpretable than their unimodal counterparts, showing the ability of our model to automatically segregate objects from ground in complex scenes.

Sparse and Continuous Attention Mechanisms

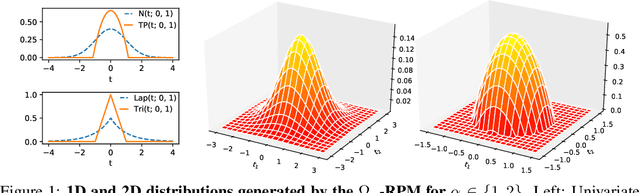
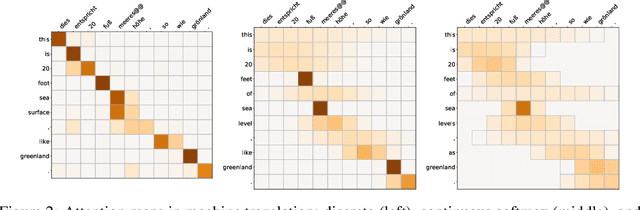
Exponential families are widely used in machine learning; they include many distributions in continuous and discrete domains (e.g., Gaussian, Dirichlet, Poisson, and categorical distributions via the softmax transformation). Distributions in each of these families have fixed support. In contrast, for finite domains, there has been recent work on sparse alternatives to softmax (e.g. sparsemax and alpha-entmax), which have varying support, being able to assign zero probability to irrelevant categories. This paper expands that work in two directions: first, we extend alpha-entmax to continuous domains, revealing a link with Tsallis statistics and deformed exponential families. Second, we introduce continuous-domain attention mechanisms, deriving efficient gradient backpropagation algorithms for alpha in {1,2}. Experiments on attention-based text classification, machine translation, and visual question answering illustrate the use of continuous attention in 1D and 2D, showing that it allows attending to time intervals and compact regions.

Seeing without Looking: Contextual Rescoring of Object Detections for AP Maximization

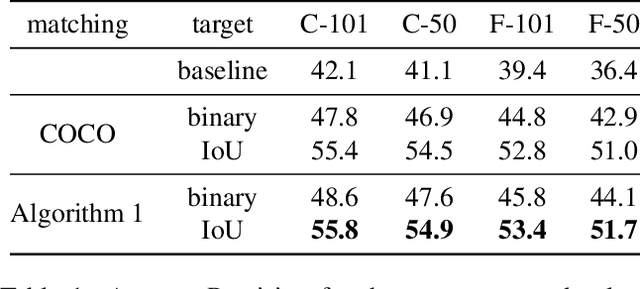
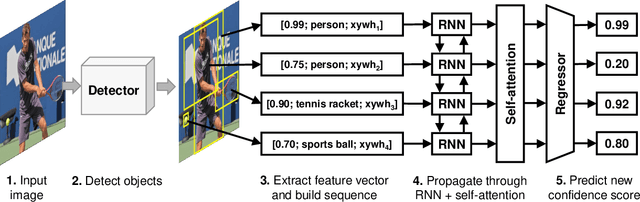
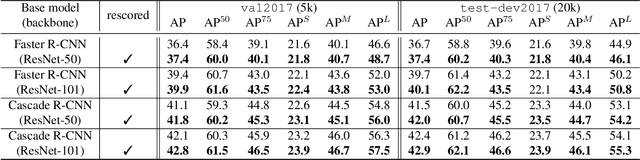
The majority of current object detectors lack context: class predictions are made independently from other detections. We propose to incorporate context in object detection by post-processing the output of an arbitrary detector to rescore the confidences of its detections. Rescoring is done by conditioning on contextual information from the entire set of detections: their confidences, predicted classes, and positions. We show that AP can be improved by simply reassigning the detection confidence values such that true positives that survive longer (i.e., those with the correct class and large IoU) are scored higher than false positives or detections with small IoU. In this setting, we use a bidirectional RNN with attention for contextual rescoring and introduce a training target that uses the IoU with ground truth to maximize AP for the given set of detections. The fact that our approach does not require access to visual features makes it computationally inexpensive and agnostic to the detection architecture. In spite of this simplicity, our model consistently improves AP over strong pre-trained baselines (Cascade R-CNN and Faster R-CNN with several backbones), particularly by reducing the confidence of duplicate detections (a learned form of non-maximum suppression) and removing out-of-context objects by conditioning on the confidences, classes, positions, and sizes of the co-occurrent detections (e.g., a high-confidence detection of bird makes a detection of sports ball less likely).

Alternating Directions Dual Decomposition

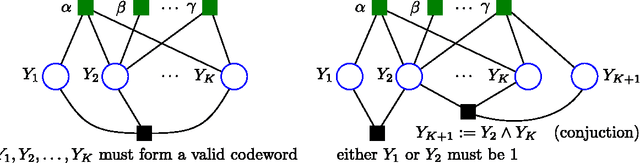
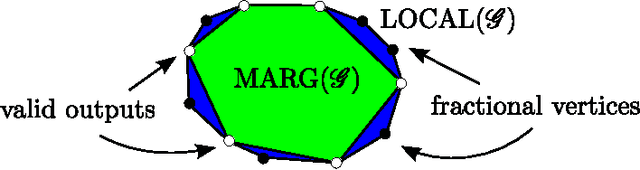
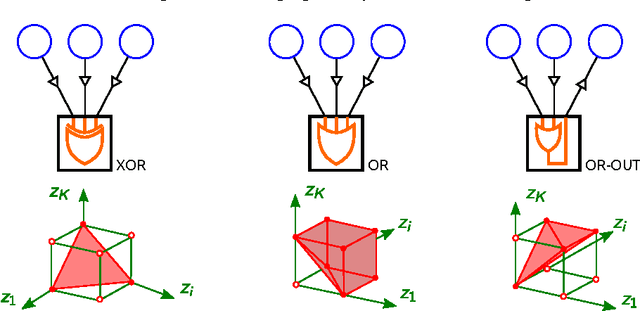
We propose AD3, a new algorithm for approximate maximum a posteriori (MAP) inference on factor graphs based on the alternating directions method of multipliers. Like dual decomposition algorithms, AD3 uses worker nodes to iteratively solve local subproblems and a controller node to combine these local solutions into a global update. The key characteristic of AD3 is that each local subproblem has a quadratic regularizer, leading to a faster consensus than subgradient-based dual decomposition, both theoretically and in practice. We provide closed-form solutions for these AD3 subproblems for binary pairwise factors and factors imposing first-order logic constraints. For arbitrary factors (large or combinatorial), we introduce an active set method which requires only an oracle for computing a local MAP configuration, making AD3 applicable to a wide range of problems. Experiments on synthetic and realworld problems show that AD3 compares favorably with the state-of-the-art.

Connectivity-Enforcing Hough Transform for the Robust Extraction of Line Segments

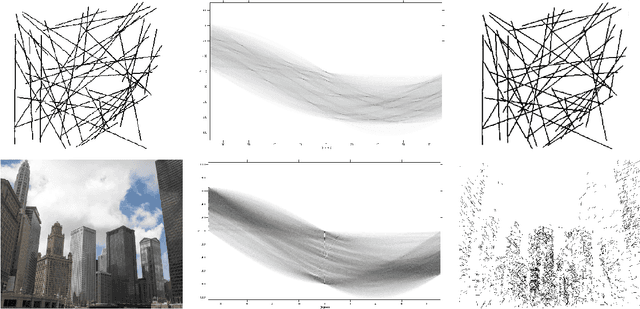
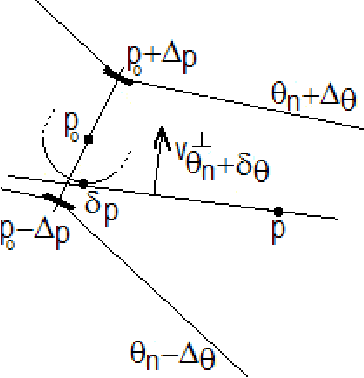
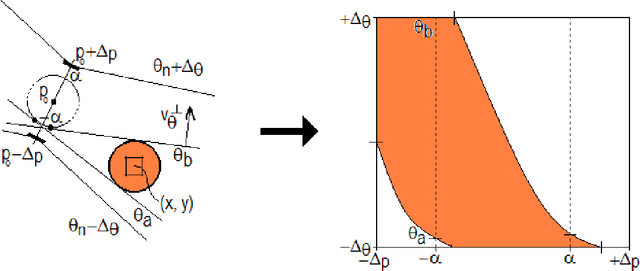
Global voting schemes based on the Hough transform (HT) have been widely used to robustly detect lines in images. However, since the votes do not take line connectivity into account, these methods do not deal well with cluttered images. In opposition, the so-called local methods enforce connectivity but lack robustness to deal with challenging situations that occur in many realistic scenarios, e.g., when line segments cross or when long segments are corrupted. In this paper, we address the critical limitations of the HT as a line segment extractor by incorporating connectivity in the voting process. This is done by only accounting for the contributions of edge points lying in increasingly larger neighborhoods and whose position and directional content agree with potential line segments. As a result, our method, which we call STRAIGHT (Segment exTRAction by connectivity-enforcInG HT), extracts the longest connected segments in each location of the image, thus also integrating into the HT voting process the usually separate step of individual segment extraction. The usage of the Hough space mapping and a corresponding hierarchical implementation make our approach computationally feasible. We present experiments that illustrate, with synthetic and real images, how STRAIGHT succeeds in extracting complete segments in several situations where current methods fail.

ANSIG - An Analytic Signature for Arbitrary 2D Shapes (or Bags of Unlabeled Points)

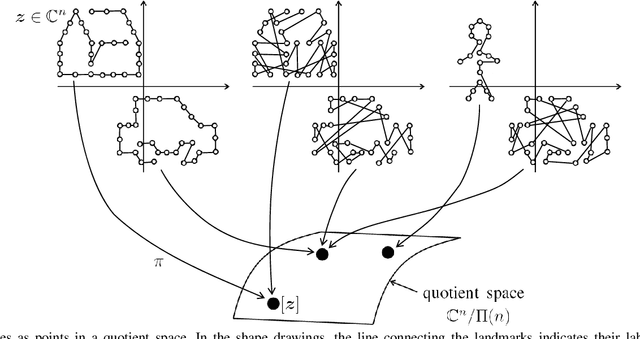
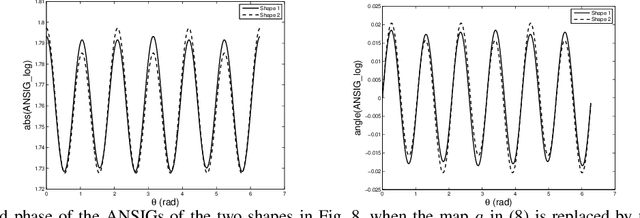
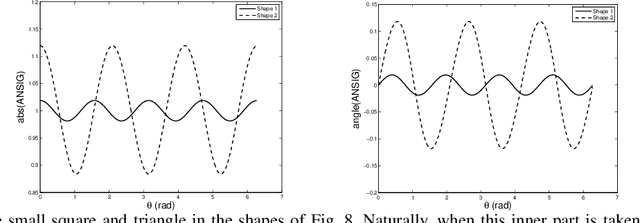
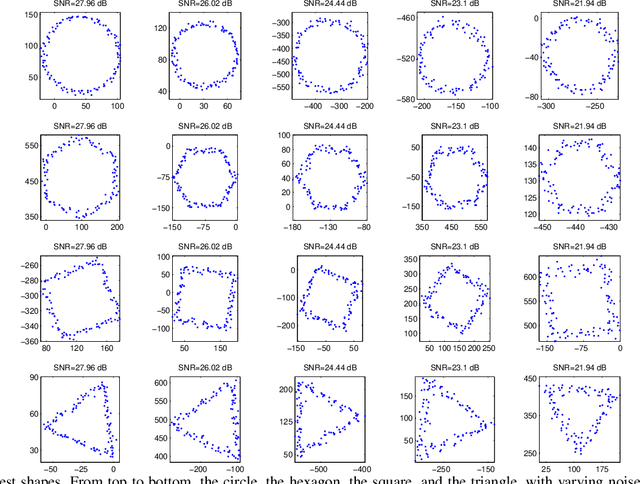
In image analysis, many tasks require representing two-dimensional (2D) shape, often specified by a set of 2D points, for comparison purposes. The challenge of the representation is that it must not only capture the characteristics of the shape but also be invariant to relevant transformations. Invariance to geometric transformations, such as translation, rotation, and scale, has received attention in the past, usually under the assumption that the points are previously labeled, i.e., that the shape is characterized by an ordered set of landmarks. However, in many practical scenarios, the points describing the shape are obtained from automatic processes, e.g., edge or corner detection, thus without labels or natural ordering. Obviously, the combinatorial problem of computing the correspondences between the points of two shapes in the presence of the aforementioned geometrical distortions becomes a quagmire when the number of points is large. We circumvent this problem by representing shapes in a way that is invariant to the permutation of the landmarks, i.e., we represent bags of unlabeled 2D points. Within our framework, a shape is mapped to an analytic function on the complex plane, leading to what we call its analytic signature (ANSIG). To store an ANSIG, it suffices to sample it along a closed contour in the complex plane. We show that the ANSIG is a maximal invariant with respect to the permutation group, i.e., that different shapes have different ANSIGs and shapes that differ by a permutation (or re-labeling) of the landmarks have the same ANSIG. We further show how easy it is to factor out geometric transformations when comparing shapes using the ANSIG representation. Finally, we illustrate these capabilities with shape-based image classification experiments.

Maximum Likelihood Mosaics

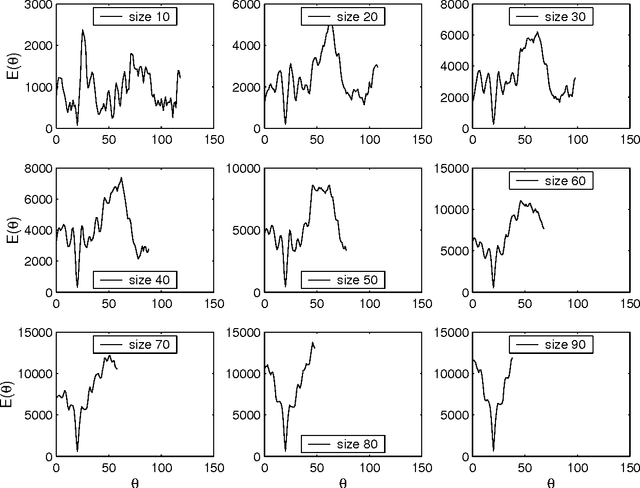
The majority of the approaches to the automatic recovery of a panoramic image from a set of partial views are suboptimal in the sense that the input images are aligned, or registered, pair by pair, e.g., consecutive frames of a video clip. These approaches lead to propagation errors that may be very severe, particularly when dealing with videos that show the same region at disjoint time intervals. Although some authors have proposed a post-processing step to reduce the registration errors in these situations, there have not been attempts to compute the optimal solution, i.e., the registrations leading to the panorama that best matches the entire set of partial views}. This is our goal. In this paper, we use a generative model for the partial views of the panorama and develop an algorithm to compute in an efficient way the Maximum Likelihood estimate of all the unknowns involved: the parameters describing the alignment of all the images and the panorama itself.

3-D Rigid Models from Partial Views - Global Factorization

The so-called factorization methods recover 3-D rigid structure from motion by factorizing an observation matrix that collects 2-D projections of features. These methods became popular due to their robustness - they use a large number of views, which constrains adequately the solution - and computational simplicity - the large number of unknowns is computed through an SVD, avoiding non-linear optimization. However, they require that all the entries of the observation matrix are known. This is unlikely to happen in practice, due to self-occlusion and limited field of view. Also, when processing long videos, regions that become occluded often appear again later. Current factorization methods process these as new regions, leading to less accurate estimates of 3-D structure. In this paper, we propose a global factorization method that infers complete 3-D models directly from the 2-D projections in the entire set of available video frames. Our method decides whether a region that has become visible is a region that was seen before, or a previously unseen region, in a global way, i.e., by seeking the simplest rigid object that describes well the entire set of observations. This global approach increases significantly the accuracy of the estimates of the 3-D shape of the scene and the 3-D motion of the camera. Experiments with artificial and real videos illustrate the good performance of our method.