José J. Rodrigues
ANSIG - An Analytic Signature for Arbitrary 2D Shapes (or Bags of Unlabeled Points)
Oct 19, 2010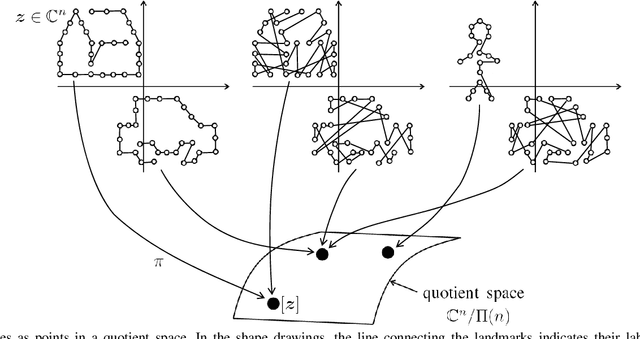
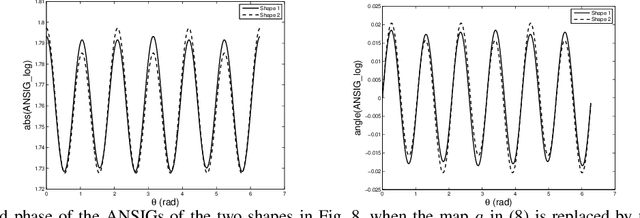
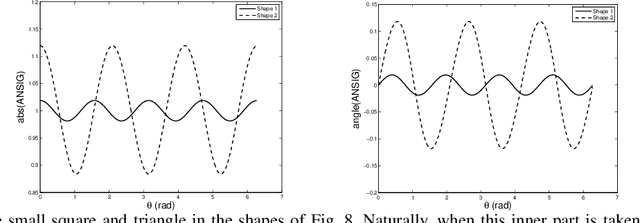
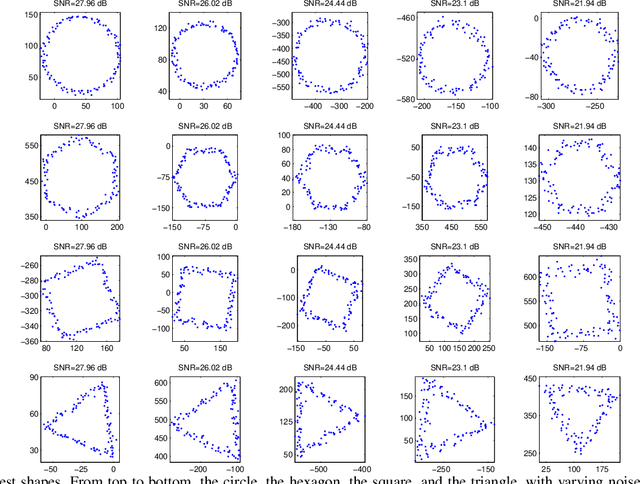
Abstract:In image analysis, many tasks require representing two-dimensional (2D) shape, often specified by a set of 2D points, for comparison purposes. The challenge of the representation is that it must not only capture the characteristics of the shape but also be invariant to relevant transformations. Invariance to geometric transformations, such as translation, rotation, and scale, has received attention in the past, usually under the assumption that the points are previously labeled, i.e., that the shape is characterized by an ordered set of landmarks. However, in many practical scenarios, the points describing the shape are obtained from automatic processes, e.g., edge or corner detection, thus without labels or natural ordering. Obviously, the combinatorial problem of computing the correspondences between the points of two shapes in the presence of the aforementioned geometrical distortions becomes a quagmire when the number of points is large. We circumvent this problem by representing shapes in a way that is invariant to the permutation of the landmarks, i.e., we represent bags of unlabeled 2D points. Within our framework, a shape is mapped to an analytic function on the complex plane, leading to what we call its analytic signature (ANSIG). To store an ANSIG, it suffices to sample it along a closed contour in the complex plane. We show that the ANSIG is a maximal invariant with respect to the permutation group, i.e., that different shapes have different ANSIGs and shapes that differ by a permutation (or re-labeling) of the landmarks have the same ANSIG. We further show how easy it is to factor out geometric transformations when comparing shapes using the ANSIG representation. Finally, we illustrate these capabilities with shape-based image classification experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge