Global MMLU: Understanding and Addressing Cultural and Linguistic Biases in Multilingual Evaluation

Cultural biases in multilingual datasets pose significant challenges for their effectiveness as global benchmarks. These biases stem not only from language but also from the cultural knowledge required to interpret questions, reducing the practical utility of translated datasets like MMLU. Furthermore, translation often introduces artifacts that can distort the meaning or clarity of questions in the target language. A common practice in multilingual evaluation is to rely on machine-translated evaluation sets, but simply translating a dataset is insufficient to address these challenges. In this work, we trace the impact of both of these issues on multilingual evaluations and ensuing model performances. Our large-scale evaluation of state-of-the-art open and proprietary models illustrates that progress on MMLU depends heavily on learning Western-centric concepts, with 28% of all questions requiring culturally sensitive knowledge. Moreover, for questions requiring geographic knowledge, an astounding 84.9% focus on either North American or European regions. Rankings of model evaluations change depending on whether they are evaluated on the full portion or the subset of questions annotated as culturally sensitive, showing the distortion to model rankings when blindly relying on translated MMLU. We release Global-MMLU, an improved MMLU with evaluation coverage across 42 languages -- with improved overall quality by engaging with compensated professional and community annotators to verify translation quality while also rigorously evaluating cultural biases present in the original dataset. This comprehensive Global-MMLU set also includes designated subsets labeled as culturally sensitive and culturally agnostic to allow for more holistic, complete evaluation.

SaulLM-7B: A pioneering Large Language Model for Law

In this paper, we introduce SaulLM-7B, a large language model (LLM) tailored for the legal domain. With 7 billion parameters, SaulLM-7B is the first LLM designed explicitly for legal text comprehension and generation. Leveraging the Mistral 7B architecture as its foundation, SaulLM-7B is trained on an English legal corpus of over 30 billion tokens. SaulLM-7B exhibits state-of-the-art proficiency in understanding and processing legal documents. Additionally, we present a novel instructional fine-tuning method that leverages legal datasets to further enhance SaulLM-7B's performance in legal tasks. SaulLM-7B is released under the MIT License.

Sparse and Structured Hopfield Networks

Modern Hopfield networks have enjoyed recent interest due to their connection to attention in transformers. Our paper provides a unified framework for sparse Hopfield networks by establishing a link with Fenchel-Young losses. The result is a new family of Hopfield-Fenchel-Young energies whose update rules are end-to-end differentiable sparse transformations. We reveal a connection between loss margins, sparsity, and exact memory retrieval. We further extend this framework to structured Hopfield networks via the SparseMAP transformation, which can retrieve pattern associations instead of a single pattern. Experiments on multiple instance learning and text rationalization demonstrate the usefulness of our approach.

Alternating Directions Dual Decomposition

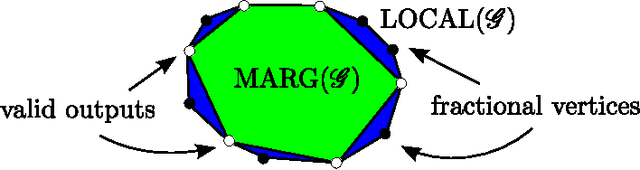
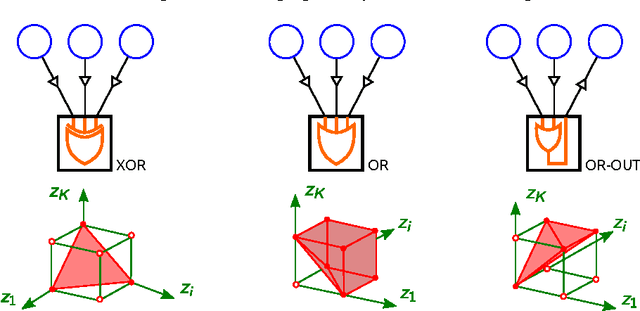
We propose AD3, a new algorithm for approximate maximum a posteriori (MAP) inference on factor graphs based on the alternating directions method of multipliers. Like dual decomposition algorithms, AD3 uses worker nodes to iteratively solve local subproblems and a controller node to combine these local solutions into a global update. The key characteristic of AD3 is that each local subproblem has a quadratic regularizer, leading to a faster consensus than subgradient-based dual decomposition, both theoretically and in practice. We provide closed-form solutions for these AD3 subproblems for binary pairwise factors and factors imposing first-order logic constraints. For arbitrary factors (large or combinatorial), we introduce an active set method which requires only an oracle for computing a local MAP configuration, making AD3 applicable to a wide range of problems. Experiments on synthetic and realworld problems show that AD3 compares favorably with the state-of-the-art.

Online Multiple Kernel Learning for Structured Prediction

Despite the recent progress towards efficient multiple kernel learning (MKL), the structured output case remains an open research front. Current approaches involve repeatedly solving a batch learning problem, which makes them inadequate for large scale scenarios. We propose a new family of online proximal algorithms for MKL (as well as for group-lasso and variants thereof), which overcomes that drawback. We show regret, convergence, and generalization bounds for the proposed method. Experiments on handwriting recognition and dependency parsing testify for the successfulness of the approach.