Hopfield-Fenchel-Young Networks: A Unified Framework for Associative Memory Retrieval

Associative memory models, such as Hopfield networks and their modern variants, have garnered renewed interest due to advancements in memory capacity and connections with self-attention in transformers. In this work, we introduce a unified framework-Hopfield-Fenchel-Young networks-which generalizes these models to a broader family of energy functions. Our energies are formulated as the difference between two Fenchel-Young losses: one, parameterized by a generalized entropy, defines the Hopfield scoring mechanism, while the other applies a post-transformation to the Hopfield output. By utilizing Tsallis and norm entropies, we derive end-to-end differentiable update rules that enable sparse transformations, uncovering new connections between loss margins, sparsity, and exact retrieval of single memory patterns. We further extend this framework to structured Hopfield networks using the SparseMAP transformation, allowing the retrieval of pattern associations rather than a single pattern. Our framework unifies and extends traditional and modern Hopfield networks and provides an energy minimization perspective for widely used post-transformations like $\ell_2$-normalization and layer normalization-all through suitable choices of Fenchel-Young losses and by using convex analysis as a building block. Finally, we validate our Hopfield-Fenchel-Young networks on diverse memory recall tasks, including free and sequential recall. Experiments on simulated data, image retrieval, multiple instance learning, and text rationalization demonstrate the effectiveness of our approach.

Sparse and Structured Hopfield Networks

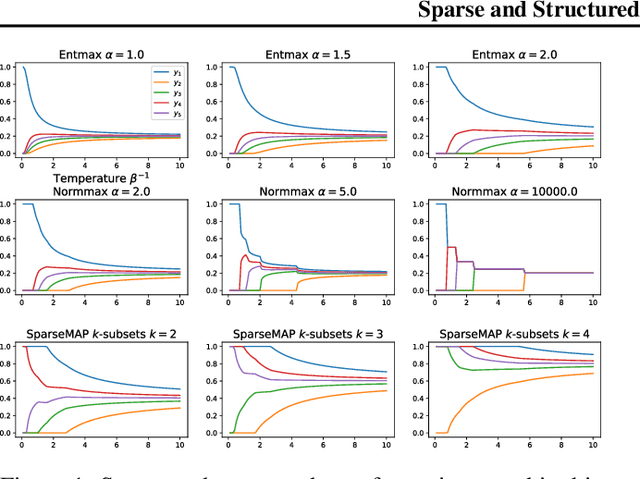
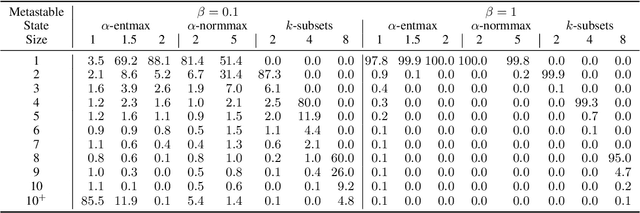
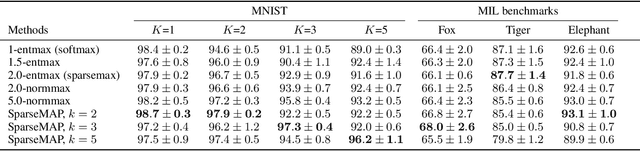
Modern Hopfield networks have enjoyed recent interest due to their connection to attention in transformers. Our paper provides a unified framework for sparse Hopfield networks by establishing a link with Fenchel-Young losses. The result is a new family of Hopfield-Fenchel-Young energies whose update rules are end-to-end differentiable sparse transformations. We reveal a connection between loss margins, sparsity, and exact memory retrieval. We further extend this framework to structured Hopfield networks via the SparseMAP transformation, which can retrieve pattern associations instead of a single pattern. Experiments on multiple instance learning and text rationalization demonstrate the usefulness of our approach.

Causal policy ranking

Policies trained via reinforcement learning (RL) are often very complex even for simple tasks. In an episode with $n$ time steps, a policy will make $n$ decisions on actions to take, many of which may appear non-intuitive to the observer. Moreover, it is not clear which of these decisions directly contribute towards achieving the reward and how significant is their contribution. Given a trained policy, we propose a black-box method based on counterfactual reasoning that estimates the causal effect that these decisions have on reward attainment and ranks the decisions according to this estimate. In this preliminary work, we compare our measure against an alternative, non-causal, ranking procedure, highlight the benefits of causality-based policy ranking, and discuss potential future work integrating causal algorithms into the interpretation of RL agent policies.

Hierarchical model-based policy optimization: from actions to action sequences and back

We develop a normative framework for hierarchical model-based policy optimization based on applying second-order methods in the space of all possible state-action paths. The resulting natural path gradient performs policy updates in a manner which is sensitive to the long-range correlational structure of the induced stationary state-action densities. We demonstrate that the natural path gradient can be computed exactly given an environment dynamics model and depends on expressions akin to higher-order successor representations. In simulation, we show that the priorization of local policy updates in the resulting policy flow indeed reflects the intuitive state-space hierarchy in several toy problems.

Characterizing optimal hierarchical policy inference on graphs via non-equilibrium thermodynamics

Hierarchies are of fundamental interest in both stochastic optimal control and biological control due to their facilitation of a range of desirable computational traits in a control algorithm and the possibility that they may form a core principle of sensorimotor and cognitive control systems. However, a theoretically justified construction of state-space hierarchies over all spatial resolutions and their evolution through a policy inference process remains elusive. Here, a formalism for deriving such normative representations of discrete Markov decision processes is introduced in the context of graphs. The resulting hierarchies correspond to a hierarchical policy inference algorithm approximating a discrete gradient flow between state-space trajectory densities generated by the prior and optimal policies.