$\infty$-Video: A Training-Free Approach to Long Video Understanding via Continuous-Time Memory Consolidation

Current video-language models struggle with long-video understanding due to limited context lengths and reliance on sparse frame subsampling, often leading to information loss. This paper introduces $\infty$-Video, which can process arbitrarily long videos through a continuous-time long-term memory (LTM) consolidation mechanism. Our framework augments video Q-formers by allowing them to process unbounded video contexts efficiently and without requiring additional training. Through continuous attention, our approach dynamically allocates higher granularity to the most relevant video segments, forming "sticky" memories that evolve over time. Experiments with Video-LLaMA and VideoChat2 demonstrate improved performance in video question-answering tasks, showcasing the potential of continuous-time LTM mechanisms to enable scalable and training-free comprehension of long videos.

Hopfield-Fenchel-Young Networks: A Unified Framework for Associative Memory Retrieval

Associative memory models, such as Hopfield networks and their modern variants, have garnered renewed interest due to advancements in memory capacity and connections with self-attention in transformers. In this work, we introduce a unified framework-Hopfield-Fenchel-Young networks-which generalizes these models to a broader family of energy functions. Our energies are formulated as the difference between two Fenchel-Young losses: one, parameterized by a generalized entropy, defines the Hopfield scoring mechanism, while the other applies a post-transformation to the Hopfield output. By utilizing Tsallis and norm entropies, we derive end-to-end differentiable update rules that enable sparse transformations, uncovering new connections between loss margins, sparsity, and exact retrieval of single memory patterns. We further extend this framework to structured Hopfield networks using the SparseMAP transformation, allowing the retrieval of pattern associations rather than a single pattern. Our framework unifies and extends traditional and modern Hopfield networks and provides an energy minimization perspective for widely used post-transformations like $\ell_2$-normalization and layer normalization-all through suitable choices of Fenchel-Young losses and by using convex analysis as a building block. Finally, we validate our Hopfield-Fenchel-Young networks on diverse memory recall tasks, including free and sequential recall. Experiments on simulated data, image retrieval, multiple instance learning, and text rationalization demonstrate the effectiveness of our approach.

Sparse and Structured Hopfield Networks

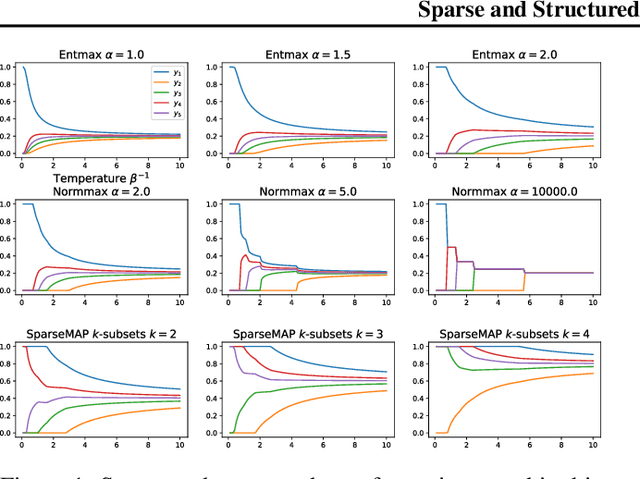
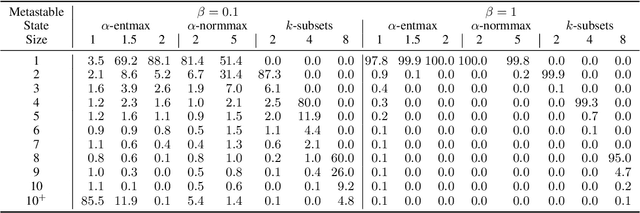
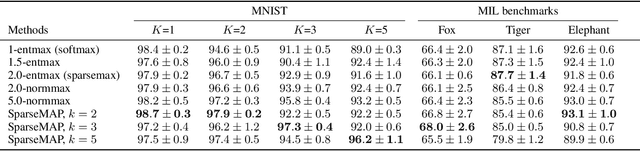
Modern Hopfield networks have enjoyed recent interest due to their connection to attention in transformers. Our paper provides a unified framework for sparse Hopfield networks by establishing a link with Fenchel-Young losses. The result is a new family of Hopfield-Fenchel-Young energies whose update rules are end-to-end differentiable sparse transformations. We reveal a connection between loss margins, sparsity, and exact memory retrieval. We further extend this framework to structured Hopfield networks via the SparseMAP transformation, which can retrieve pattern associations instead of a single pattern. Experiments on multiple instance learning and text rationalization demonstrate the usefulness of our approach.

Symplectic Momentum Neural Networks -- Using Discrete Variational Mechanics as a prior in Deep Learning

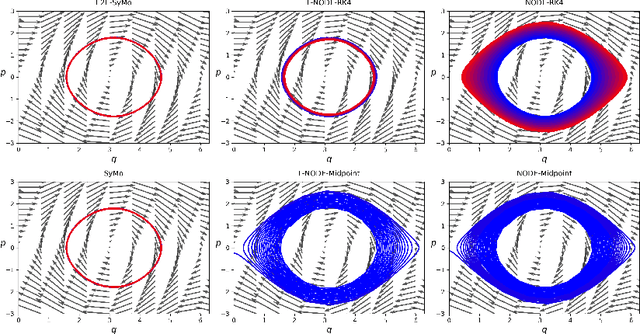
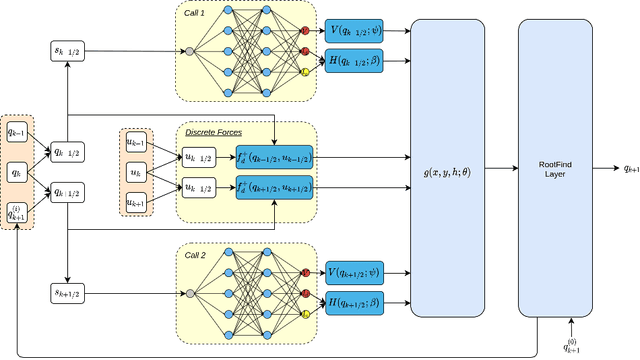
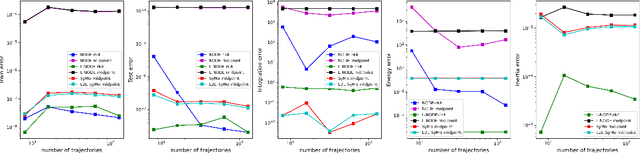
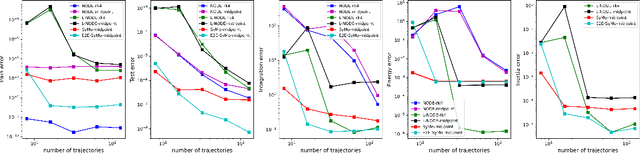
With deep learning being gaining attention from the research community for prediction and control of real physical systems, learning important representations is becoming now more than ever mandatory. It is of extremely importance that deep learning representations are coherent with physics. When learning from discrete data this can be guaranteed by including some sort of prior into the learning, however not all discretization priors preserve important structures from the physics. In this paper we introduce Symplectic Momentum Neural Networks (SyMo) as models from a discrete formulation of mechanics for non-separable mechanical systems. The combination of such formulation leads SyMos to be constrained towards preserving important geometric structures such as momentum and a symplectic form and learn from limited data. Furthermore, it allows to learn dynamics only from the poses as training data. We extend SyMos to include variational integrators within the learning framework by developing an implicit root-find layer which leads to End-to-End Symplectic Momentum Neural Networks (E2E-SyMo). Through experimental results, using the pendulum and cartpole we show that such combination not only allows these models tol earn from limited data but also provides the models with the capability of preserving the symplectic form and show better long-term behaviour.