MM1.5: Methods, Analysis & Insights from Multimodal LLM Fine-tuning

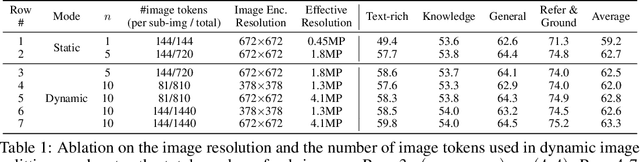
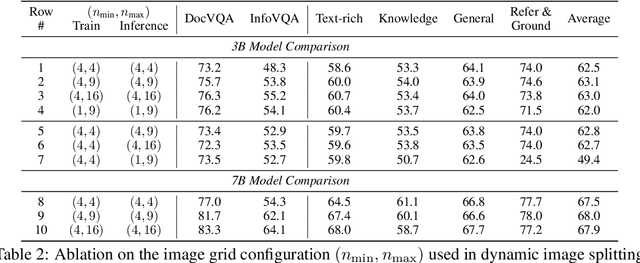
We present MM1.5, a new family of multimodal large language models (MLLMs) designed to enhance capabilities in text-rich image understanding, visual referring and grounding, and multi-image reasoning. Building upon the MM1 architecture, MM1.5 adopts a data-centric approach to model training, systematically exploring the impact of diverse data mixtures across the entire model training lifecycle. This includes high-quality OCR data and synthetic captions for continual pre-training, as well as an optimized visual instruction-tuning data mixture for supervised fine-tuning. Our models range from 1B to 30B parameters, encompassing both dense and mixture-of-experts (MoE) variants, and demonstrate that careful data curation and training strategies can yield strong performance even at small scales (1B and 3B). Additionally, we introduce two specialized variants: MM1.5-Video, designed for video understanding, and MM1.5-UI, tailored for mobile UI understanding. Through extensive empirical studies and ablations, we provide detailed insights into the training processes and decisions that inform our final designs, offering valuable guidance for future research in MLLM development.

MM1: Methods, Analysis & Insights from Multimodal LLM Pre-training

In this work, we discuss building performant Multimodal Large Language Models (MLLMs). In particular, we study the importance of various architecture components and data choices. Through careful and comprehensive ablations of the image encoder, the vision language connector, and various pre-training data choices, we identified several crucial design lessons. For example, we demonstrate that for large-scale multimodal pre-training using a careful mix of image-caption, interleaved image-text, and text-only data is crucial for achieving state-of-the-art (SOTA) few-shot results across multiple benchmarks, compared to other published pre-training results. Further, we show that the image encoder together with image resolution and the image token count has substantial impact, while the vision-language connector design is of comparatively negligible importance. By scaling up the presented recipe, we build MM1, a family of multimodal models up to 30B parameters, including both dense models and mixture-of-experts (MoE) variants, that are SOTA in pre-training metrics and achieve competitive performance after supervised fine-tuning on a range of established multimodal benchmarks. Thanks to large-scale pre-training, MM1 enjoys appealing properties such as enhanced in-context learning, and multi-image reasoning, enabling few-shot chain-of-thought prompting.

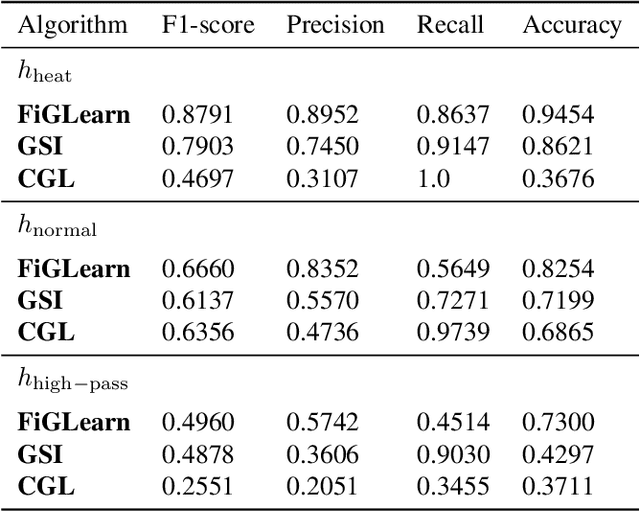
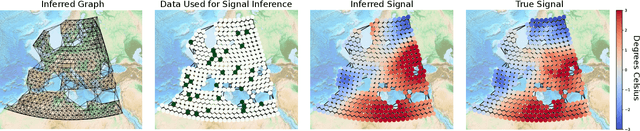
FiGLearn: Filter and Graph Learning using Optimal Transport

In many applications, a dataset can be considered as a set of observed signals that live on an unknown underlying graph structure. Some of these signals may be seen as white noise that has been filtered on the graph topology by a graph filter. Hence, the knowledge of the filter and the graph provides valuable information about the underlying data generation process and the complex interactions that arise in the dataset. We hence introduce a novel graph signal processing framework for jointly learning the graph and its generating filter from signal observations. We cast a new optimisation problem that minimises the Wasserstein distance between the distribution of the signal observations and the filtered signal distribution model. Our proposed method outperforms state-of-the-art graph learning frameworks on synthetic data. We then apply our method to a temperature anomaly dataset, and further show how this framework can be used to infer missing values if only very little information is available.

Sequential Mode Estimation with Oracle Queries

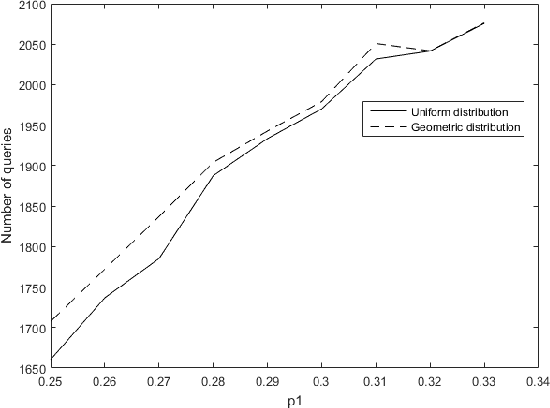
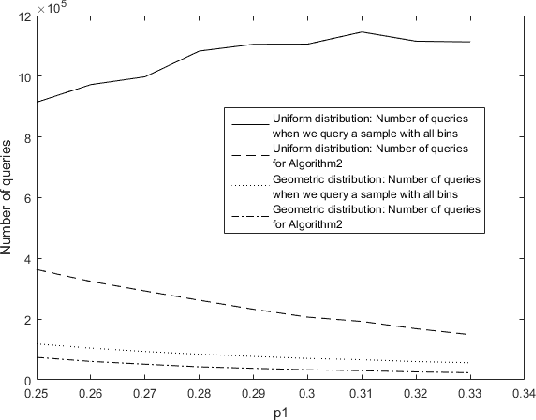
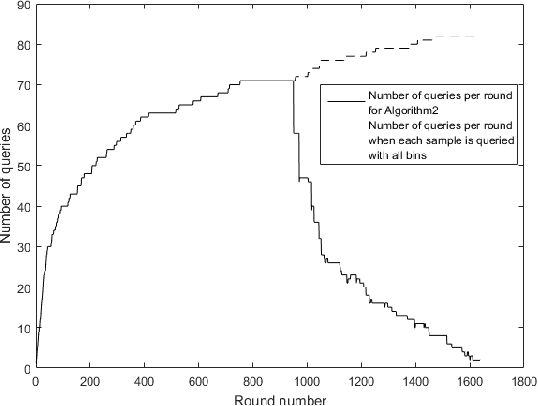
We consider the problem of adaptively PAC-learning a probability distribution $\mathcal{P}$'s mode by querying an oracle for information about a sequence of i.i.d. samples $X_1, X_2, \ldots$ generated from $\mathcal{P}$. We consider two different query models: (a) each query is an index $i$ for which the oracle reveals the value of the sample $X_i$, (b) each query is comprised of two indices $i$ and $j$ for which the oracle reveals if the samples $X_i$ and $X_j$ are the same or not. For these query models, we give sequential mode-estimation algorithms which, at each time $t$, either make a query to the corresponding oracle based on past observations, or decide to stop and output an estimate for the distribution's mode, required to be correct with a specified confidence. We analyze the query complexity of these algorithms for any underlying distribution $\mathcal{P}$, and derive corresponding lower bounds on the optimal query complexity under the two querying models.