Sequential Mode Estimation with Oracle Queries
Paper and Code
Nov 19, 2019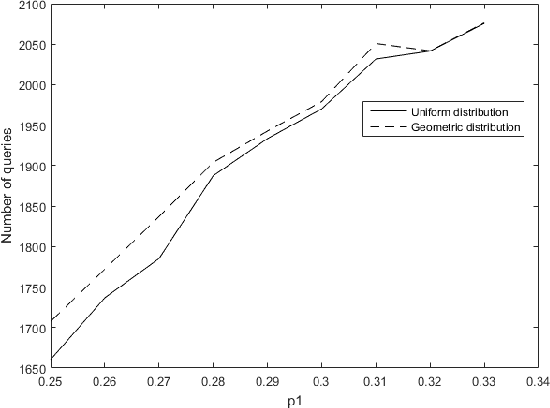
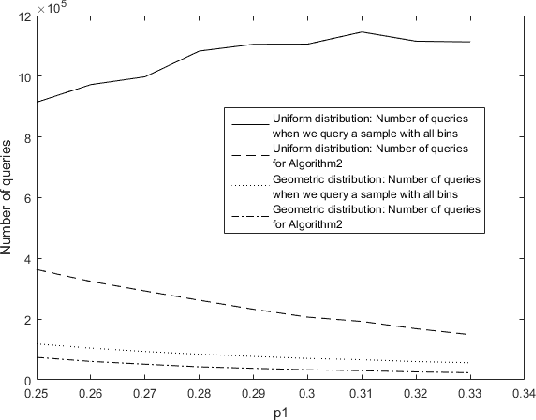
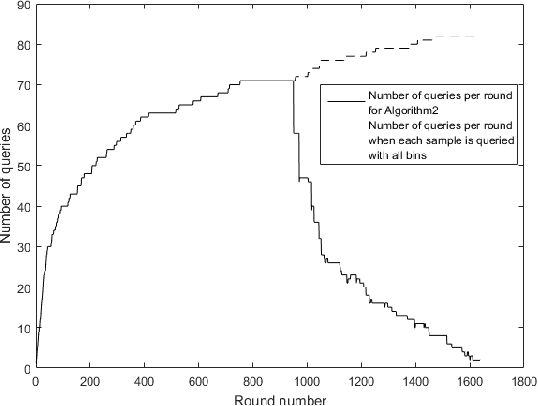
We consider the problem of adaptively PAC-learning a probability distribution $\mathcal{P}$'s mode by querying an oracle for information about a sequence of i.i.d. samples $X_1, X_2, \ldots$ generated from $\mathcal{P}$. We consider two different query models: (a) each query is an index $i$ for which the oracle reveals the value of the sample $X_i$, (b) each query is comprised of two indices $i$ and $j$ for which the oracle reveals if the samples $X_i$ and $X_j$ are the same or not. For these query models, we give sequential mode-estimation algorithms which, at each time $t$, either make a query to the corresponding oracle based on past observations, or decide to stop and output an estimate for the distribution's mode, required to be correct with a specified confidence. We analyze the query complexity of these algorithms for any underlying distribution $\mathcal{P}$, and derive corresponding lower bounds on the optimal query complexity under the two querying models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge