Matthias Minder
FiGLearn: Filter and Graph Learning using Optimal Transport
Oct 29, 2020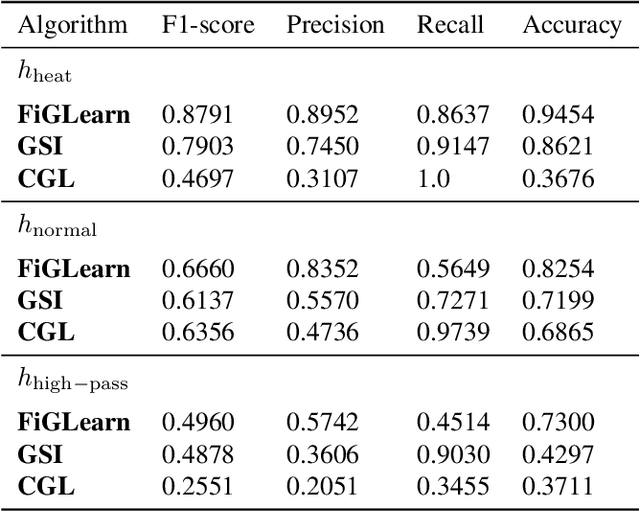
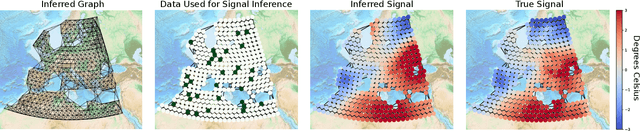
Abstract:In many applications, a dataset can be considered as a set of observed signals that live on an unknown underlying graph structure. Some of these signals may be seen as white noise that has been filtered on the graph topology by a graph filter. Hence, the knowledge of the filter and the graph provides valuable information about the underlying data generation process and the complex interactions that arise in the dataset. We hence introduce a novel graph signal processing framework for jointly learning the graph and its generating filter from signal observations. We cast a new optimisation problem that minimises the Wasserstein distance between the distribution of the signal observations and the filtered signal distribution model. Our proposed method outperforms state-of-the-art graph learning frameworks on synthetic data. We then apply our method to a temperature anomaly dataset, and further show how this framework can be used to infer missing values if only very little information is available.
Wasserstein-based Graph Alignment
Mar 12, 2020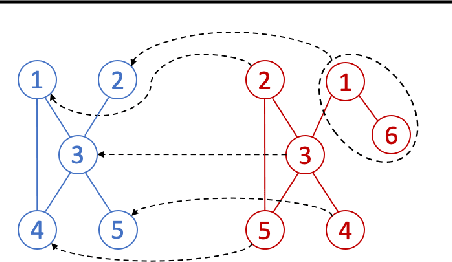
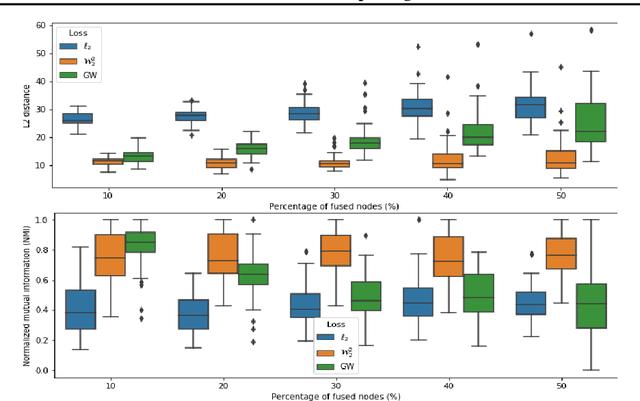

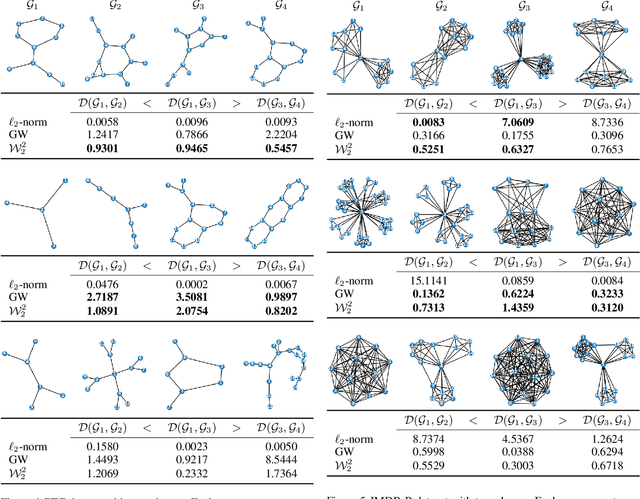
Abstract:We propose a novel method for comparing non-aligned graphs of different sizes, based on the Wasserstein distance between graph signal distributions induced by the respective graph Laplacian matrices. Specifically, we cast a new formulation for the one-to-many graph alignment problem, which aims at matching a node in the smaller graph with one or more nodes in the larger graph. By integrating optimal transport in our graph comparison framework, we generate both a structurally-meaningful graph distance, and a signal transportation plan that models the structure of graph data. The resulting alignment problem is solved with stochastic gradient descent, where we use a novel Dykstra operator to ensure that the solution is a one-to-many (soft) assignment matrix. We demonstrate the performance of our novel framework on graph alignment and graph classification, and we show that our method leads to significant improvements with respect to the state-of-the-art algorithms for each of these tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge