Graph learning under sparsity priors
Paper and Code
Jul 18, 2017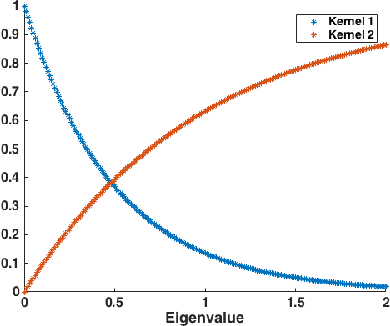
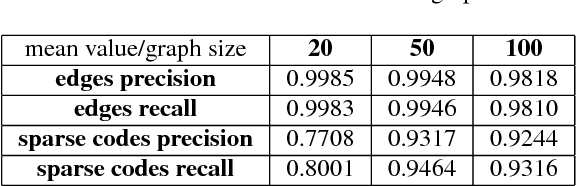

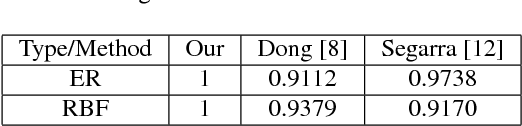
Graph signals offer a very generic and natural representation for data that lives on networks or irregular structures. The actual data structure is however often unknown a priori but can sometimes be estimated from the knowledge of the application domain. If this is not possible, the data structure has to be inferred from the mere signal observations. This is exactly the problem that we address in this paper, under the assumption that the graph signals can be represented as a sparse linear combination of a few atoms of a structured graph dictionary. The dictionary is constructed on polynomials of the graph Laplacian, which can sparsely represent a general class of graph signals composed of localized patterns on the graph. We formulate a graph learning problem, whose solution provides an ideal fit between the signal observations and the sparse graph signal model. As the problem is non-convex, we propose to solve it by alternating between a signal sparse coding and a graph update step. We provide experimental results that outline the good graph recovery performance of our method, which generally compares favourably to other recent network inference algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge