Targeted synthetic data generation for tabular data via hardness characterization

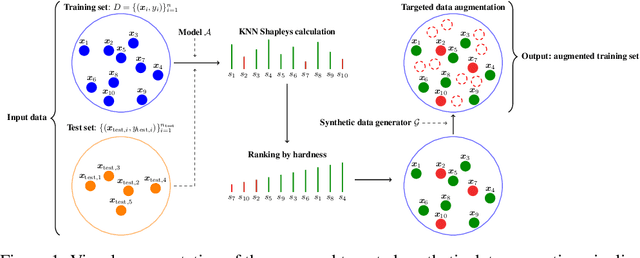
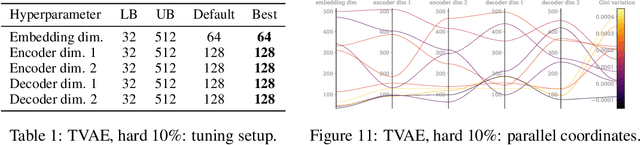
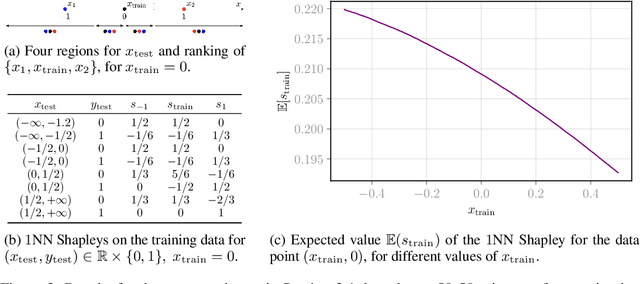
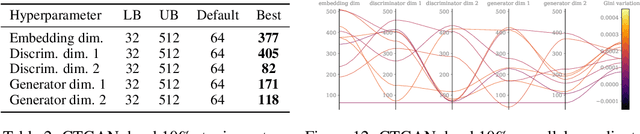
Synthetic data generation has been proven successful in improving model performance and robustness in the context of scarce or low-quality data. Using the data valuation framework to statistically identify beneficial and detrimental observations, we introduce a novel augmentation pipeline that generates only high-value training points based on hardness characterization. We first demonstrate via benchmarks on real data that Shapley-based data valuation methods perform comparably with learning-based methods in hardness characterisation tasks, while offering significant theoretical and computational advantages. Then, we show that synthetic data generators trained on the hardest points outperform non-targeted data augmentation on simulated data and on a large scale credit default prediction task. In particular, our approach improves the quality of out-of-sample predictions and it is computationally more efficient compared to non-targeted methods.

Approximate learning of parsimonious Bayesian context trees

Models for categorical sequences typically assume exchangeable or first-order dependent sequence elements. These are common assumptions, for example, in models of computer malware traces and protein sequences. Although such simplifying assumptions lead to computational tractability, these models fail to capture long-range, complex dependence structures that may be harnessed for greater predictive power. To this end, a Bayesian modelling framework is proposed to parsimoniously capture rich dependence structures in categorical sequences, with memory efficiency suitable for real-time processing of data streams. Parsimonious Bayesian context trees are introduced as a form of variable-order Markov model with conjugate prior distributions. The novel framework requires fewer parameters than fixed-order Markov models by dropping redundant dependencies and clustering sequential contexts. Approximate inference on the context tree structure is performed via a computationally efficient model-based agglomerative clustering procedure. The proposed framework is tested on synthetic and real-world data examples, and it outperforms existing sequence models when fitted to real protein sequences and honeypot computer terminal sessions.

Extended Deep Adaptive Input Normalization for Preprocessing Time Series Data for Neural Networks

Data preprocessing is a crucial part of any machine learning pipeline, and it can have a significant impact on both performance and training efficiency. This is especially evident when using deep neural networks for time series prediction and classification: real-world time series data often exhibit irregularities such as multi-modality, skewness and outliers, and the model performance can degrade rapidly if these characteristics are not adequately addressed. In this work, we propose the EDAIN (Extended Deep Adaptive Input Normalization) layer, a novel adaptive neural layer that learns how to appropriately normalize irregular time series data for a given task in an end-to-end fashion, instead of using a fixed normalization scheme. This is achieved by optimizing its unknown parameters simultaneously with the deep neural network using back-propagation. Our experiments, conducted using synthetic data, a credit default prediction dataset, and a large-scale limit order book benchmark dataset, demonstrate the superior performance of the EDAIN layer when compared to conventional normalization methods and existing adaptive time series preprocessing layers.

Latent structure blockmodels for Bayesian spectral graph clustering

Spectral embedding of network adjacency matrices often produces node representations living approximately around low-dimensional submanifold structures. In particular, hidden substructure is expected to arise when the graph is generated from a latent position model. Furthermore, the presence of communities within the network might generate community-specific submanifold structures in the embedding, but this is not explicitly accounted for in most statistical models for networks. In this article, a class of models called latent structure block models (LSBM) is proposed to address such scenarios, allowing for graph clustering when community-specific one dimensional manifold structure is present. LSBMs focus on a specific class of latent space model, the random dot product graph (RDPG), and assign a latent submanifold to the latent positions of each community. A Bayesian model for the embeddings arising from LSBMs is discussed, and shown to have a good performance on simulated and real world network data. The model is able to correctly recover the underlying communities living in a one-dimensional manifold, even when the parametric form of the underlying curves is unknown, achieving remarkable results on a variety of real data.

Mutually exciting point process graphs for modelling dynamic networks

A new class of models for dynamic networks is proposed, called mutually exciting point process graphs (MEG), motivated by a practical application in computer network security. MEG is a scalable network-wide statistical model for point processes with dyadic marks, which can be used for anomaly detection when assessing the significance of previously unobserved connections. The model combines mutually exciting point processes to estimate dependencies between events and latent space models to infer relationships between the nodes. The intensity functions for each network edge are parameterised exclusively by node-specific parameters, which allows information to be shared across the network. Fast inferential procedures using modern gradient ascent algorithms are exploited. The model is tested on simulated graphs and real world computer network datasets, demonstrating excellent performance.

Spectral clustering on spherical coordinates under the degree-corrected stochastic blockmodel

Spectral clustering is a popular method for community detection in networks under the assumption of the standard stochastic blockmodel. Taking a matrix representation of the graph such as the adjacency matrix, the nodes are clustered on a low dimensional projection obtained from a truncated spectral decomposition of the matrix. Estimating the number of communities and the dimension of the reduced latent space well is crucial for good performance of spectral clustering algorithms. Real-world networks, such as computer networks studied in cyber-security applications, often present heterogeneous within-community degree distributions which are better addressed by the degree-corrected stochastic blockmodel. A novel, model-based method is proposed in this article for simultaneous and automated selection of the number of communities and latent dimension for spectral clustering under the degree-corrected stochastic blockmodel. The method is based on a transformation to spherical coordinates of the spectral embedding, and on a novel modelling assumption in the transformed space, which is then embedded into an existing model selection framework for estimating the number of communities and the latent dimension. Results show improved performance over competing methods on simulated and real-world computer network data.

Bayesian estimation of the latent dimension and communities in stochastic blockmodels

Spectral embedding of adjacency or Laplacian matrices of undirected graphs is a common technique for representing a network in a lower dimensional latent space, with optimal theoretical guarantees. The embedding can be used to estimate the community structure of the network, with strong consistency results in the stochastic blockmodel framework. One of the main practical limitations of standard algorithms for community detection from spectral embeddings is that the number of communities and the latent dimension of the embedding must be specified in advance. In this article, a novel Bayesian model for simultaneous and automatic selection of the appropriate dimension of the latent space and the number of blocks is proposed. Extensions to directed and bipartite graphs are discussed. The model is tested on simulated and real world network data, showing promising performance for recovering latent community structure.