Vertex nomination: The canonical sampling and the extended spectral nomination schemes

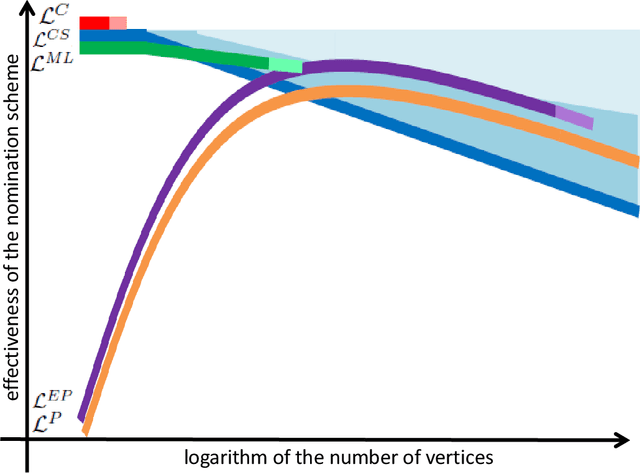
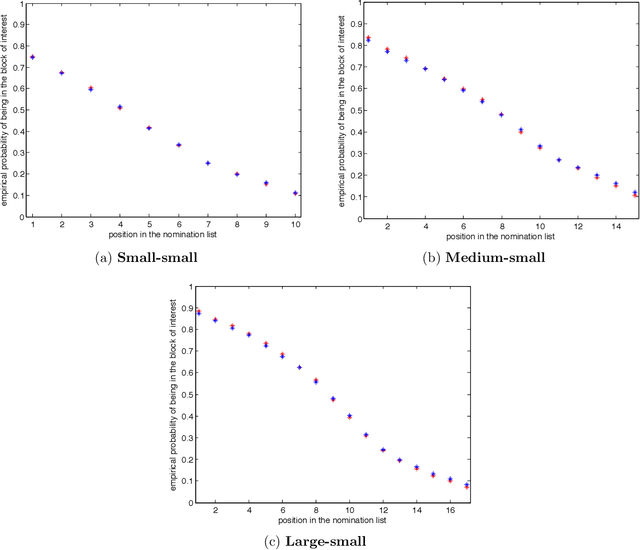
Suppose that one particular block in a stochastic block model is deemed "interesting," but block labels are only observed for a few of the vertices. Utilizing a graph realized from the model, the vertex nomination task is to order the vertices with unobserved block labels into a "nomination list" with the goal of having an abundance of interesting vertices near the top of the list. In this paper we extend and enhance two basic vertex nomination schemes; the canonical nomination scheme ${\mathcal L}^C$ and the spectral partitioning nomination scheme ${\mathcal L}^P$. The canonical nomination scheme ${\mathcal L}^C$ is provably optimal, but is computationally intractable, being impractical to implement even on modestly sized graphs. With this in mind, we introduce a scalable, Markov chain Monte Carlo-based nomination scheme, called the {\it canonical sampling nomination scheme} ${\mathcal L}^{CS}$, that converges to the canonical nomination scheme ${\mathcal L}^{C}$ as the amount of sampling goes to infinity. We also introduce a novel spectral partitioning nomination scheme called the {\it extended spectral partitioning nomination scheme} ${\mathcal L}^{EP}$. Real-data and simulation experiments are employed to illustrate the effectiveness of these vertex nomination schemes, as well as their empirical computational complexity.