Jordan Yoder
Vertex nomination: The canonical sampling and the extended spectral nomination schemes
Feb 14, 2018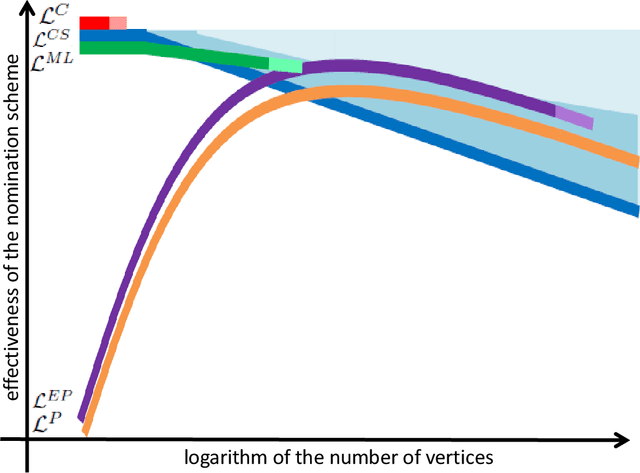
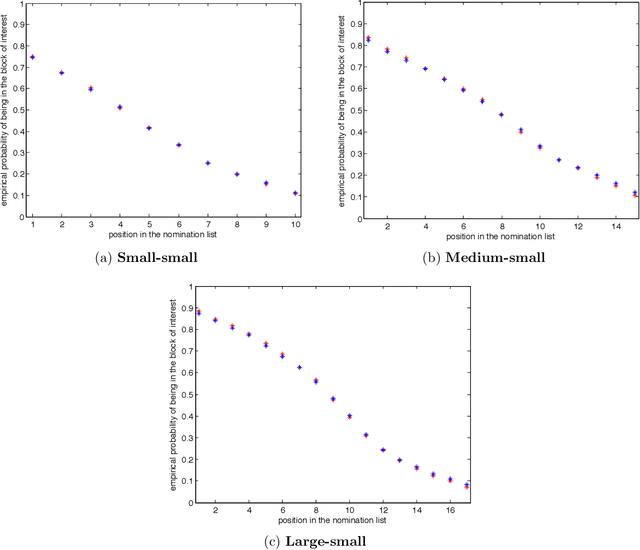
Abstract:Suppose that one particular block in a stochastic block model is deemed "interesting," but block labels are only observed for a few of the vertices. Utilizing a graph realized from the model, the vertex nomination task is to order the vertices with unobserved block labels into a "nomination list" with the goal of having an abundance of interesting vertices near the top of the list. In this paper we extend and enhance two basic vertex nomination schemes; the canonical nomination scheme ${\mathcal L}^C$ and the spectral partitioning nomination scheme ${\mathcal L}^P$. The canonical nomination scheme ${\mathcal L}^C$ is provably optimal, but is computationally intractable, being impractical to implement even on modestly sized graphs. With this in mind, we introduce a scalable, Markov chain Monte Carlo-based nomination scheme, called the {\it canonical sampling nomination scheme} ${\mathcal L}^{CS}$, that converges to the canonical nomination scheme ${\mathcal L}^{C}$ as the amount of sampling goes to infinity. We also introduce a novel spectral partitioning nomination scheme called the {\it extended spectral partitioning nomination scheme} ${\mathcal L}^{EP}$. Real-data and simulation experiments are employed to illustrate the effectiveness of these vertex nomination schemes, as well as their empirical computational complexity.
Semi-supervised K-means++
Feb 01, 2016


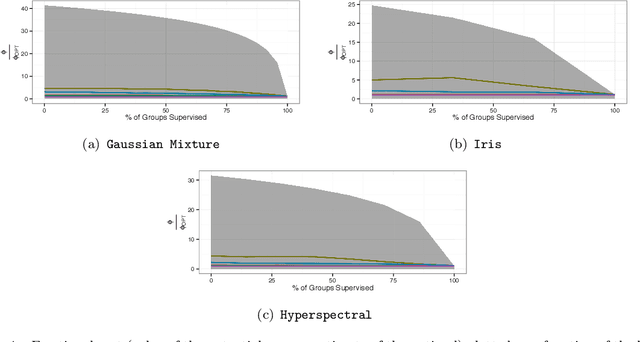
Abstract:Traditionally, practitioners initialize the {\tt k-means} algorithm with centers chosen uniformly at random. Randomized initialization with uneven weights ({\tt k-means++}) has recently been used to improve the performance over this strategy in cost and run-time. We consider the k-means problem with semi-supervised information, where some of the data are pre-labeled, and we seek to label the rest according to the minimum cost solution. By extending the {\tt k-means++} algorithm and analysis to account for the labels, we derive an improved theoretical bound on expected cost and observe improved performance in simulated and real data examples. This analysis provides theoretical justification for a roughly linear semi-supervised clustering algorithm.
On latent position inference from doubly stochastic messaging activities
Apr 25, 2013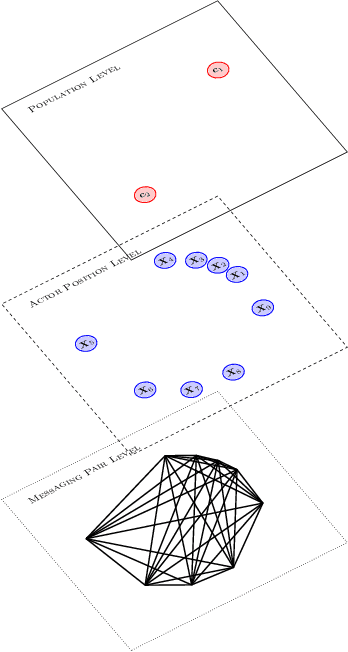

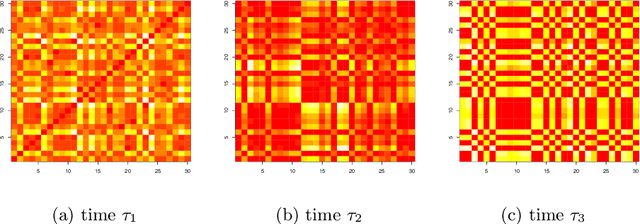
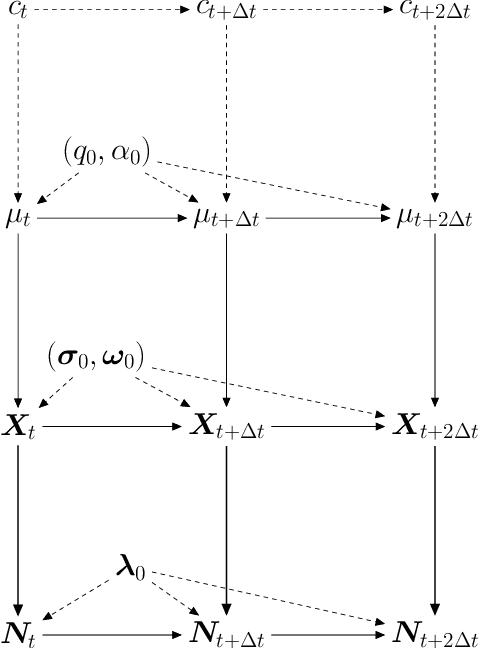
Abstract:We model messaging activities as a hierarchical doubly stochastic point process with three main levels, and develop an iterative algorithm for inferring actors' relative latent positions from a stream of messaging activity data. Each of the message-exchanging actors is modeled as a process in a latent space. The actors' latent positions are assumed to be influenced by the distribution of a much larger population over the latent space. Each actor's movement in the latent space is modeled as being governed by two parameters that we call confidence and visibility, in addition to dependence on the population distribution. The messaging frequency between a pair of actors is assumed to be inversely proportional to the distance between their latent positions. Our inference algorithm is based on a projection approach to an online filtering problem. The algorithm associates each actor with a probability density-valued process, and each probability density is assumed to be a mixture of basis functions. For efficient numerical experiments, we further develop our algorithm for the case where the basis functions are obtained by translating and scaling a standard Gaussian density.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge