On latent position inference from doubly stochastic messaging activities

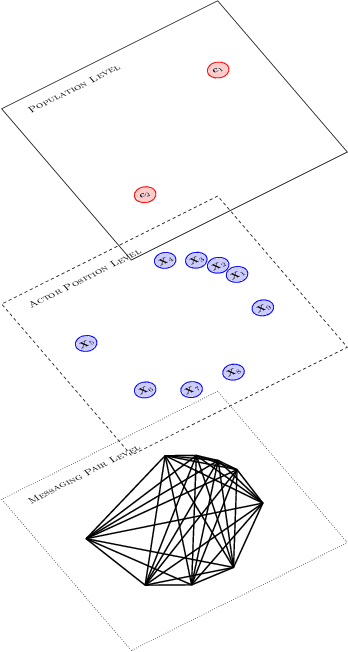
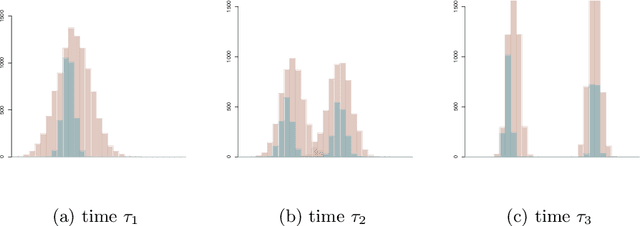
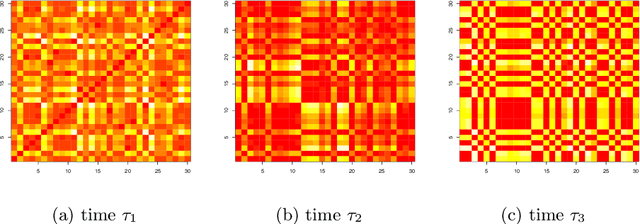
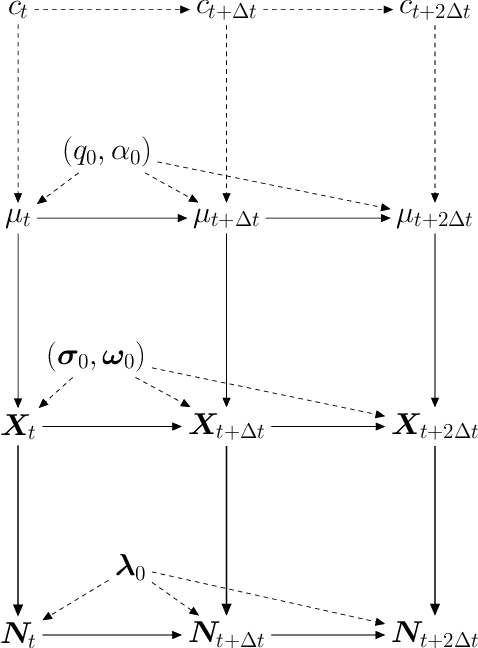
We model messaging activities as a hierarchical doubly stochastic point process with three main levels, and develop an iterative algorithm for inferring actors' relative latent positions from a stream of messaging activity data. Each of the message-exchanging actors is modeled as a process in a latent space. The actors' latent positions are assumed to be influenced by the distribution of a much larger population over the latent space. Each actor's movement in the latent space is modeled as being governed by two parameters that we call confidence and visibility, in addition to dependence on the population distribution. The messaging frequency between a pair of actors is assumed to be inversely proportional to the distance between their latent positions. Our inference algorithm is based on a projection approach to an online filtering problem. The algorithm associates each actor with a probability density-valued process, and each probability density is assumed to be a mixture of basis functions. For efficient numerical experiments, we further develop our algorithm for the case where the basis functions are obtained by translating and scaling a standard Gaussian density.