Polarity is all you need to learn and transfer faster

Natural intelligences (NIs) thrive in a dynamic world - they learn quickly, sometimes with only a few samples. In contrast, Artificial intelligences (AIs) typically learn with prohibitive amount of training samples and computational power. What design principle difference between NI and AI could contribute to such a discrepancy? Here, we propose an angle from weight polarity: development processes initialize NIs with advantageous polarity configurations; as NIs grow and learn, synapse magnitudes update yet polarities are largely kept unchanged. We demonstrate with simulation and image classification tasks that if weight polarities are adequately set $\textit{a priori}$, then networks learn with less time and data. We also explicitly illustrate situations in which $\textit{a priori}$ setting the weight polarities is disadvantageous for networks. Our work illustrates the value of weight polarities from the perspective of statistical and computational efficiency during learning.

Why Do Networks Need Negative Weights?

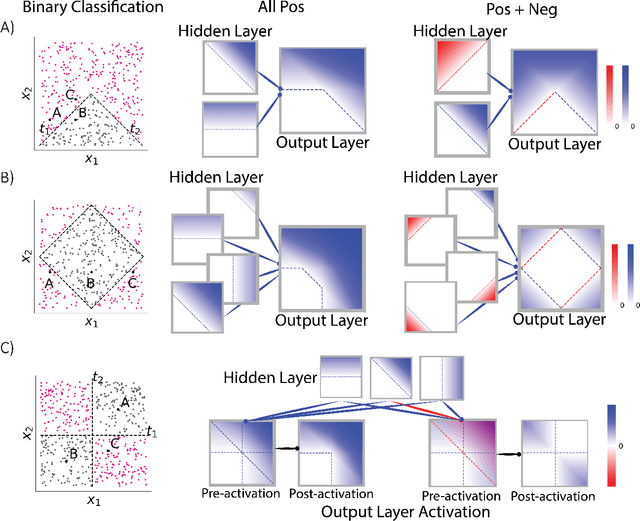
Why do networks have negative weights at all? The answer is: to learn more functions. We mathematically prove that deep neural networks with all non-negative weights are not universal approximators. This fundamental result is assumed by much of the deep learning literature without previously proving the result and demonstrating its necessity.

Discovering and Deciphering Relationships Across Disparate Data Modalities

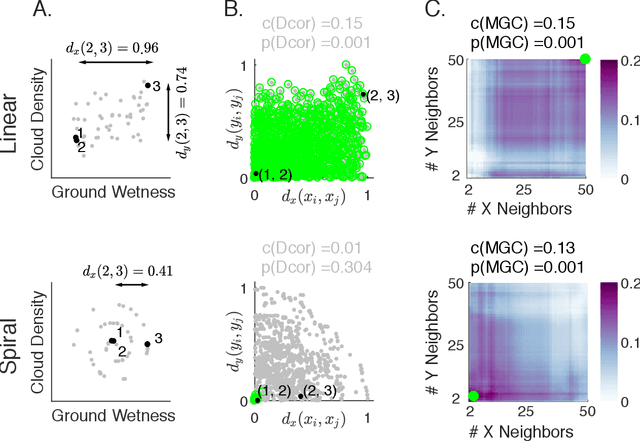
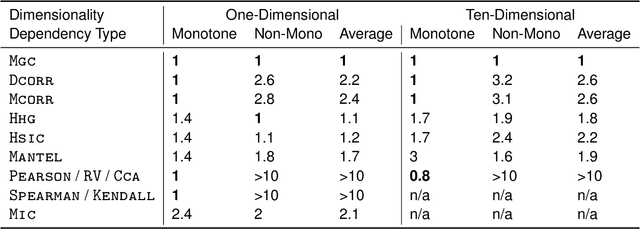
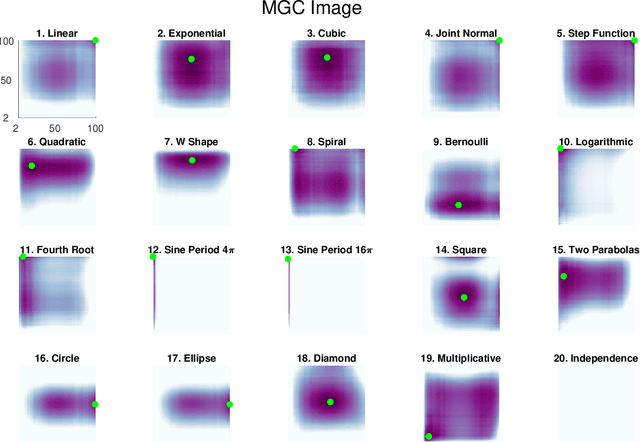
Understanding the relationships between different properties of data, such as whether a connectome or genome has information about disease status, is becoming increasingly important in modern biological datasets. While existing approaches can test whether two properties are related, they often require unfeasibly large sample sizes in real data scenarios, and do not provide any insight into how or why the procedure reached its decision. Our approach, "Multiscale Graph Correlation" (MGC), is a dependence test that juxtaposes previously disparate data science techniques, including k-nearest neighbors, kernel methods (such as support vector machines), and multiscale analysis (such as wavelets). Other methods typically require double or triple the number samples to achieve the same statistical power as MGC in a benchmark suite including high-dimensional and nonlinear relationships - spanning polynomial (linear, quadratic, cubic), trigonometric (sinusoidal, circular, ellipsoidal, spiral), geometric (square, diamond, W-shape), and other functions, with dimensionality ranging from 1 to 1000. Moreover, MGC uniquely provides a simple and elegant characterization of the potentially complex latent geometry underlying the relationship, providing insight while maintaining computational efficiency. In several real data applications, including brain imaging and cancer genetics, MGC is the only method that can both detect the presence of a dependency and provide specific guidance for the next experiment and/or analysis to conduct.

On a 'Two Truths' Phenomenon in Spectral Graph Clustering

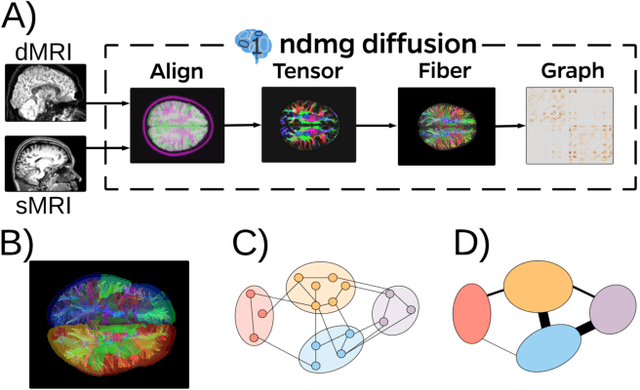
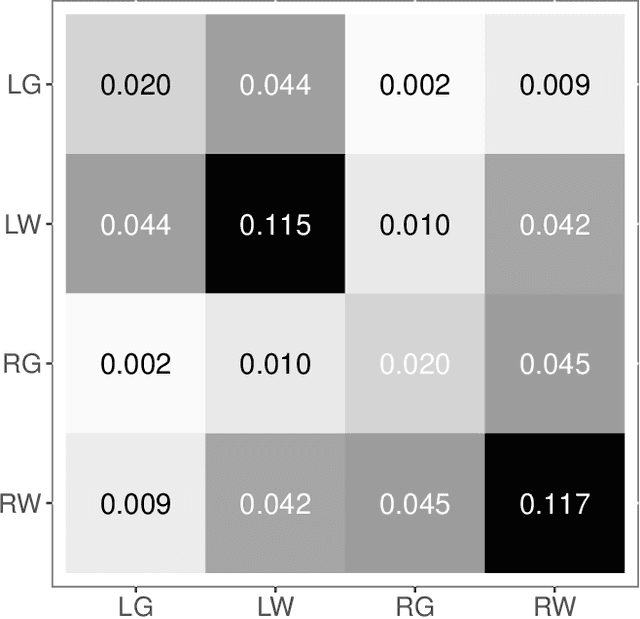
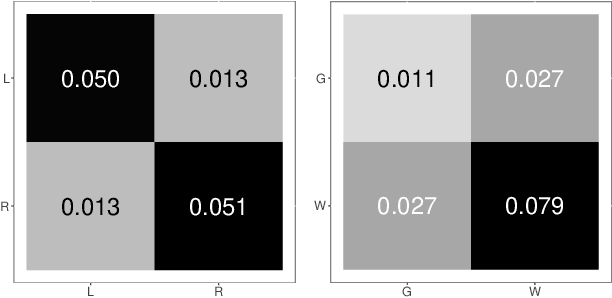
Clustering is concerned with coherently grouping observations without any explicit concept of true groupings. Spectral graph clustering - clustering the vertices of a graph based on their spectral embedding - is commonly approached via K-means (or, more generally, Gaussian mixture model) clustering composed with either Laplacian or Adjacency spectral embedding (LSE or ASE). Recent theoretical results provide new understanding of the problem and solutions, and lead us to a 'Two Truths' LSE vs. ASE spectral graph clustering phenomenon convincingly illustrated here via a diffusion MRI connectome data set: the different embedding methods yield different clustering results, with LSE capturing left hemisphere/right hemisphere affinity structure and ASE capturing gray matter/white matter core-periphery structure.

Linear Optimal Low Rank Projection for High-Dimensional Multi-Class Data

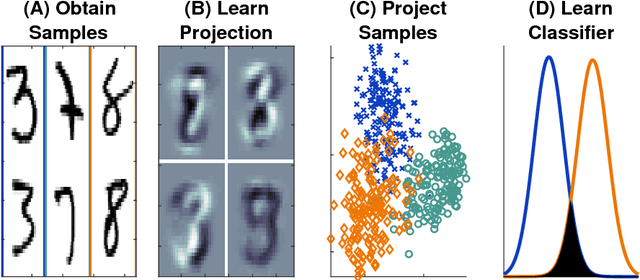
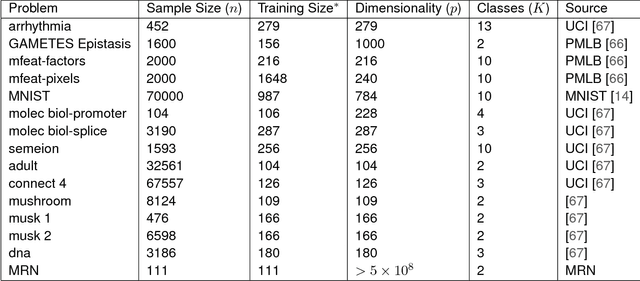
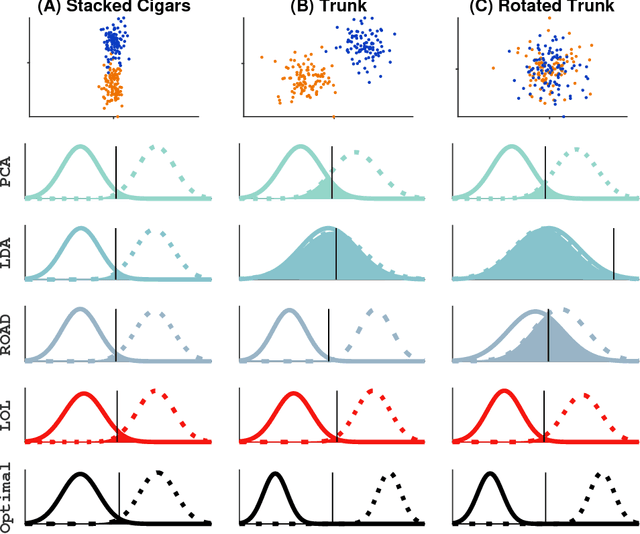
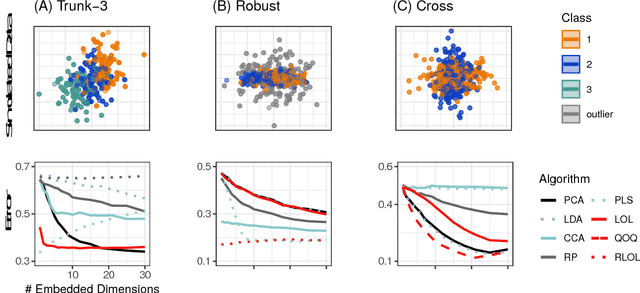
Classifying samples into categories becomes intractable when a single sample can have millions to billions of features, such as in genetics or imaging data. Principal Components Analysis (PCA) is widely used to identify a low-dimensional representation of such features for further analysis. However, PCA ignores class labels, such as whether or not a subject has cancer, thereby discarding information that could substantially improve downstream classification performance. We describe an approach, "Linear Optimal Low-rank" projection (LOL), which extends PCA by incorporating the class labels in a fashion that is advantageous over existing supervised dimensionality reduction techniques. We prove, and substantiate with synthetic experiments, that LOL leads to a better representation of the data for subsequent classification than other linear approaches, while adding negligible computational cost. We then demonstrate that LOL substantially outperforms PCA in differentiating cancer patients from healthy controls using genetic data, and in differentiating gender using magnetic resonance imaging data with $>$500 million features and 400 gigabytes of data. LOL therefore allows the solution of previous intractable problems, yet requires only a few minutes to run on a desktop computer.

Vertex nomination: The canonical sampling and the extended spectral nomination schemes

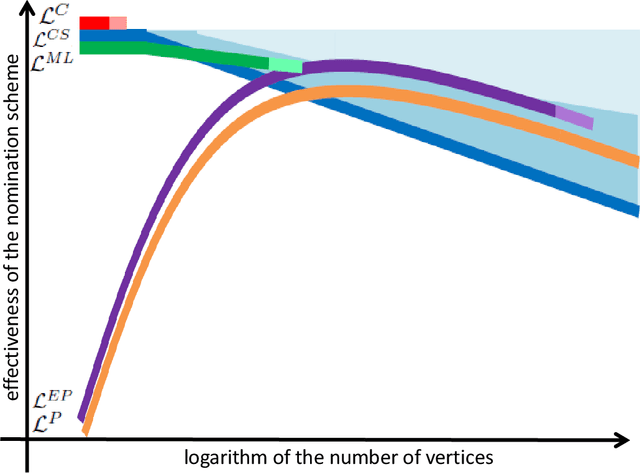
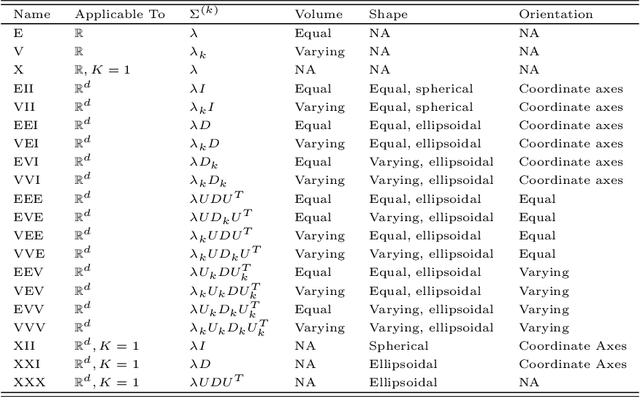
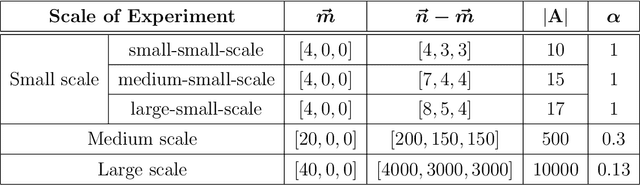
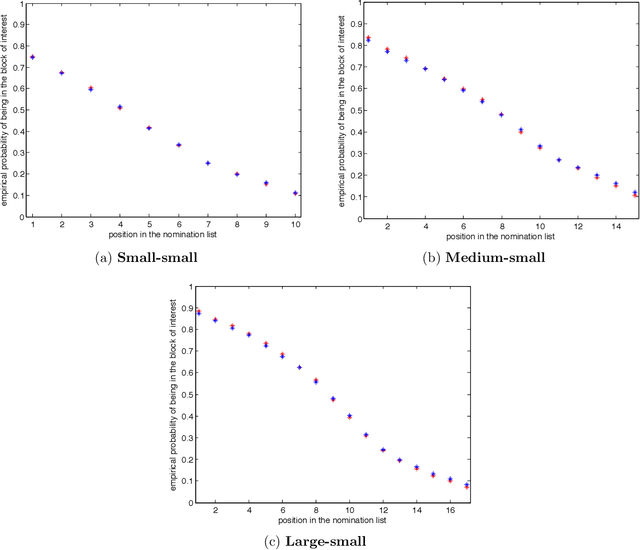
Suppose that one particular block in a stochastic block model is deemed "interesting," but block labels are only observed for a few of the vertices. Utilizing a graph realized from the model, the vertex nomination task is to order the vertices with unobserved block labels into a "nomination list" with the goal of having an abundance of interesting vertices near the top of the list. In this paper we extend and enhance two basic vertex nomination schemes; the canonical nomination scheme ${\mathcal L}^C$ and the spectral partitioning nomination scheme ${\mathcal L}^P$. The canonical nomination scheme ${\mathcal L}^C$ is provably optimal, but is computationally intractable, being impractical to implement even on modestly sized graphs. With this in mind, we introduce a scalable, Markov chain Monte Carlo-based nomination scheme, called the {\it canonical sampling nomination scheme} ${\mathcal L}^{CS}$, that converges to the canonical nomination scheme ${\mathcal L}^{C}$ as the amount of sampling goes to infinity. We also introduce a novel spectral partitioning nomination scheme called the {\it extended spectral partitioning nomination scheme} ${\mathcal L}^{EP}$. Real-data and simulation experiments are employed to illustrate the effectiveness of these vertex nomination schemes, as well as their empirical computational complexity.