Donniell Fishkind
Vertex nomination: The canonical sampling and the extended spectral nomination schemes
Feb 14, 2018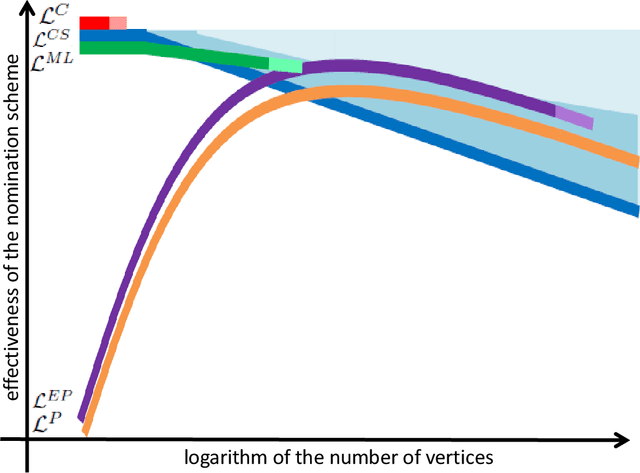
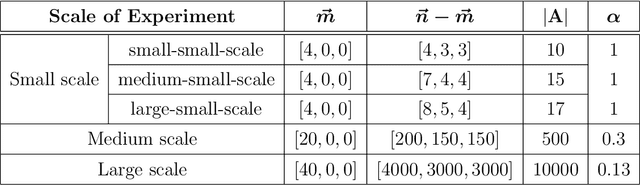
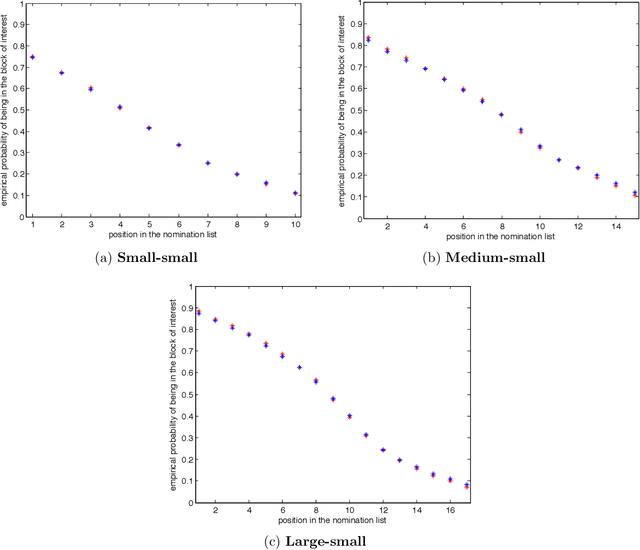
Abstract:Suppose that one particular block in a stochastic block model is deemed "interesting," but block labels are only observed for a few of the vertices. Utilizing a graph realized from the model, the vertex nomination task is to order the vertices with unobserved block labels into a "nomination list" with the goal of having an abundance of interesting vertices near the top of the list. In this paper we extend and enhance two basic vertex nomination schemes; the canonical nomination scheme ${\mathcal L}^C$ and the spectral partitioning nomination scheme ${\mathcal L}^P$. The canonical nomination scheme ${\mathcal L}^C$ is provably optimal, but is computationally intractable, being impractical to implement even on modestly sized graphs. With this in mind, we introduce a scalable, Markov chain Monte Carlo-based nomination scheme, called the {\it canonical sampling nomination scheme} ${\mathcal L}^{CS}$, that converges to the canonical nomination scheme ${\mathcal L}^{C}$ as the amount of sampling goes to infinity. We also introduce a novel spectral partitioning nomination scheme called the {\it extended spectral partitioning nomination scheme} ${\mathcal L}^{EP}$. Real-data and simulation experiments are employed to illustrate the effectiveness of these vertex nomination schemes, as well as their empirical computational complexity.
Graph Matching: Relax at Your Own Risk
Jan 10, 2015
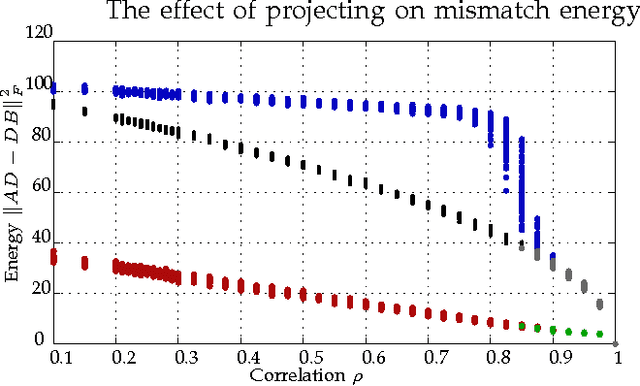
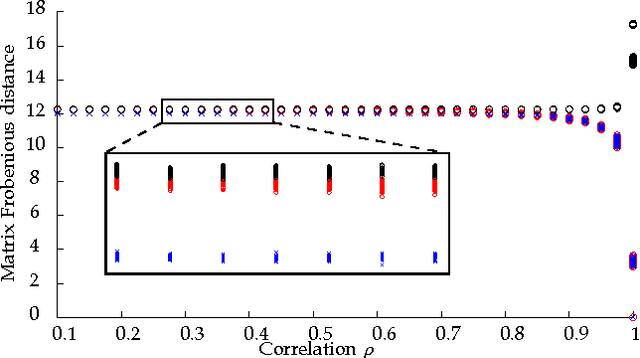
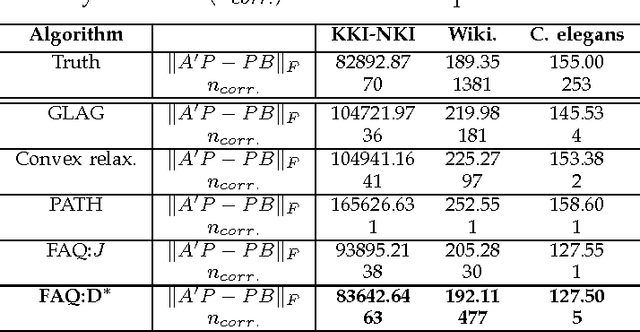
Abstract:Graph matching---aligning a pair of graphs to minimize their edge disagreements---has received wide-spread attention from both theoretical and applied communities over the past several decades, including combinatorics, computer vision, and connectomics. Its attention can be partially attributed to its computational difficulty. Although many heuristics have previously been proposed in the literature to approximately solve graph matching, very few have any theoretical support for their performance. A common technique is to relax the discrete problem to a continuous problem, therefore enabling practitioners to bring gradient-descent-type algorithms to bear. We prove that an indefinite relaxation (when solved exactly) almost always discovers the optimal permutation, while a common convex relaxation almost always fails to discover the optimal permutation. These theoretical results suggest that initializing the indefinite algorithm with the convex optimum might yield improved practical performance. Indeed, experimental results illuminate and corroborate these theoretical findings, demonstrating that excellent results are achieved in both benchmark and real data problems by amalgamating the two approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge