Graph Matching: Relax at Your Own Risk
Paper and Code
Jan 10, 2015
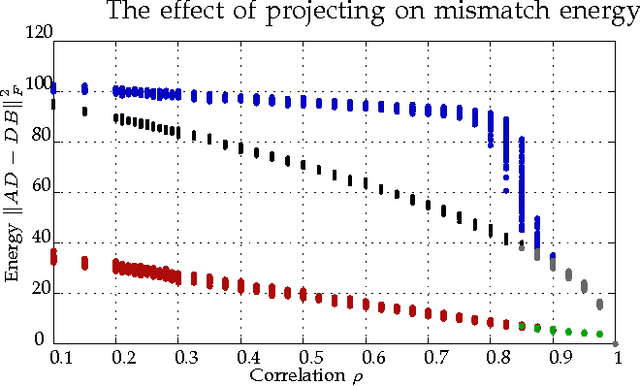
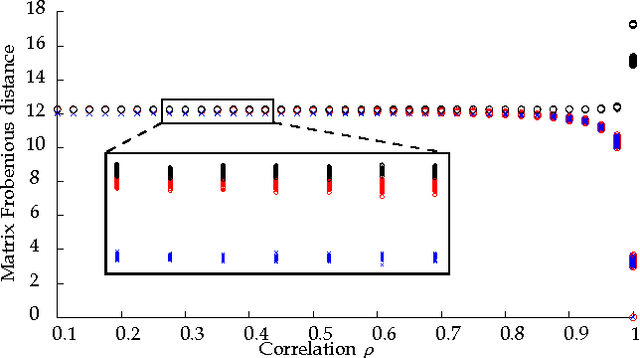
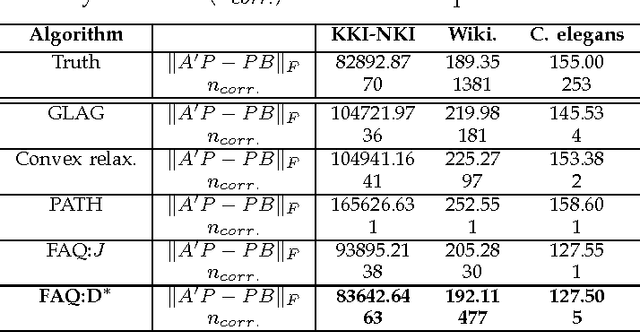
Graph matching---aligning a pair of graphs to minimize their edge disagreements---has received wide-spread attention from both theoretical and applied communities over the past several decades, including combinatorics, computer vision, and connectomics. Its attention can be partially attributed to its computational difficulty. Although many heuristics have previously been proposed in the literature to approximately solve graph matching, very few have any theoretical support for their performance. A common technique is to relax the discrete problem to a continuous problem, therefore enabling practitioners to bring gradient-descent-type algorithms to bear. We prove that an indefinite relaxation (when solved exactly) almost always discovers the optimal permutation, while a common convex relaxation almost always fails to discover the optimal permutation. These theoretical results suggest that initializing the indefinite algorithm with the convex optimum might yield improved practical performance. Indeed, experimental results illuminate and corroborate these theoretical findings, demonstrating that excellent results are achieved in both benchmark and real data problems by amalgamating the two approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge