Techniques for clustering interaction data as a collection of graphs
Paper and Code
Jan 10, 2015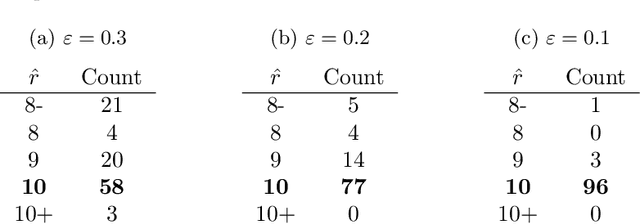

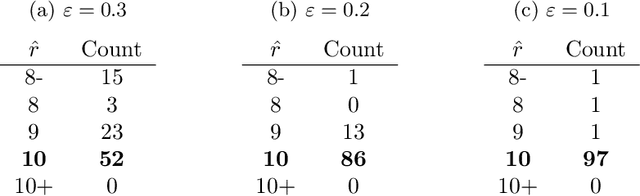

A natural approach to analyze interaction data of form "what-connects-to-what-when" is to create a time-series (or rather a sequence) of graphs through temporal discretization (bandwidth selection) and spatial discretization (vertex contraction). Such discretization together with non-negative factorization techniques can be useful for obtaining clustering of graphs. Motivating application of performing clustering of graphs (as opposed to vertex clustering) can be found in neuroscience and in social network analysis, and it can also be used to enhance community detection (i.e., vertex clustering) by way of conditioning on the cluster labels. In this paper, we formulate a problem of clustering of graphs as a model selection problem. Our approach involves information criteria, non-negative matrix factorization and singular value thresholding, and we illustrate our techniques using real and simulated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge