AD-Aligning: Emulating Human-like Generalization for Cognitive Domain Adaptation in Deep Learning

Domain adaptation is pivotal for enabling deep learning models to generalize across diverse domains, a task complicated by variations in presentation and cognitive nuances. In this paper, we introduce AD-Aligning, a novel approach that combines adversarial training with source-target domain alignment to enhance generalization capabilities. By pretraining with Coral loss and standard loss, AD-Aligning aligns target domain statistics with those of the pretrained encoder, preserving robustness while accommodating domain shifts. Through extensive experiments on diverse datasets and domain shift scenarios, including noise-induced shifts and cognitive domain adaptation tasks, we demonstrate AD-Aligning's superior performance compared to existing methods such as Deep Coral and ADDA. Our findings highlight AD-Aligning's ability to emulate the nuanced cognitive processes inherent in human perception, making it a promising solution for real-world applications requiring adaptable and robust domain adaptation strategies.

Deep Learning is Provably Robust to Symmetric Label Noise

Deep neural networks (DNNs) are capable of perfectly fitting the training data, including memorizing noisy data. It is commonly believed that memorization hurts generalization. Therefore, many recent works propose mitigation strategies to avoid noisy data or correct memorization. In this work, we step back and ask the question: Can deep learning be robust against massive label noise without any mitigation? We provide an affirmative answer for the case of symmetric label noise: We find that certain DNNs, including under-parameterized and over-parameterized models, can tolerate massive symmetric label noise up to the information-theoretic threshold. By appealing to classical statistical theory and universal consistency of DNNs, we prove that for multiclass classification, $L_1$-consistent DNN classifiers trained under symmetric label noise can achieve Bayes optimality asymptotically if the label noise probability is less than $\frac{K-1}{K}$, where $K \ge 2$ is the number of classes. Our results show that for symmetric label noise, no mitigation is necessary for $L_1$-consistent estimators. We conjecture that for general label noise, mitigation strategies that make use of the noisy data will outperform those that ignore the noisy data.

Dynamic Network Sampling for Community Detection

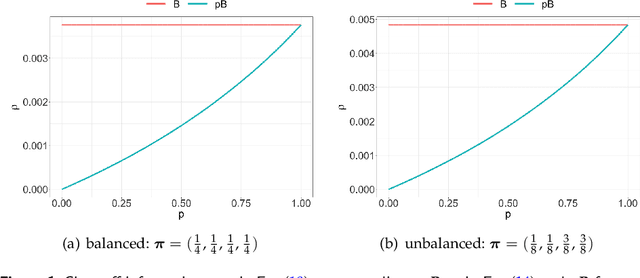
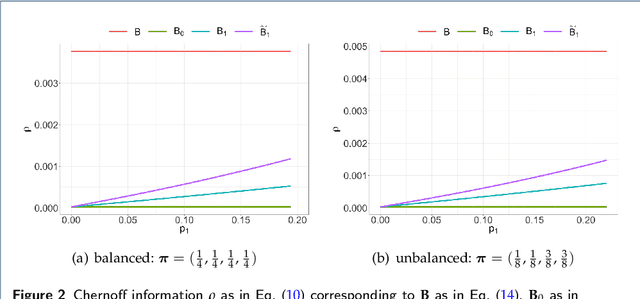
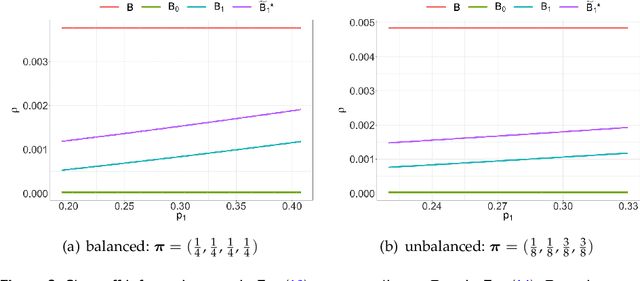
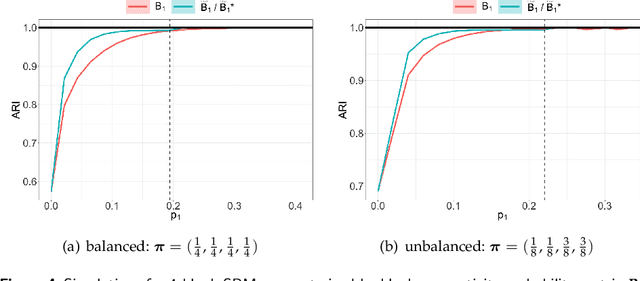
We propose a dynamic network sampling scheme to optimize block recovery for stochastic blockmodel (SBM) in the case where it is prohibitively expensive to observe the entire graph. Theoretically, we provide justification of our proposed Chernoff-optimal dynamic sampling scheme via the Chernoff information. Practically, we evaluate the performance, in terms of block recovery, of our method on several real datasets from different domains. Both theoretically and practically results suggest that our method can identify vertices that have the most impact on block structure so that one can only check whether there are edges between them to save significant resources but still recover the block structure.

Deep Learning with Label Noise: A Hierarchical Approach

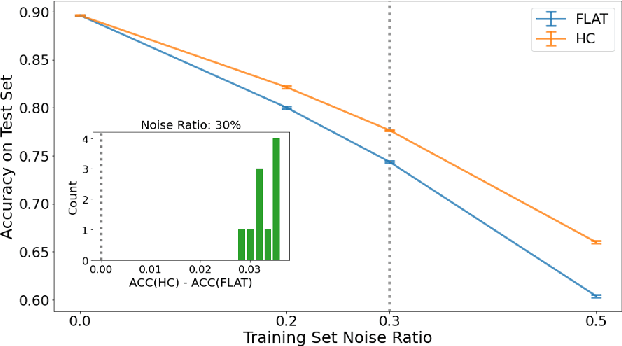
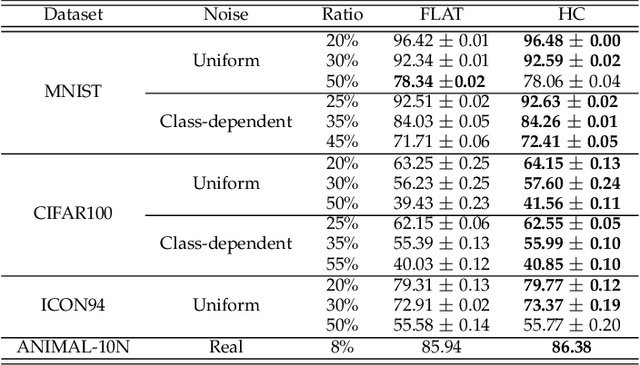
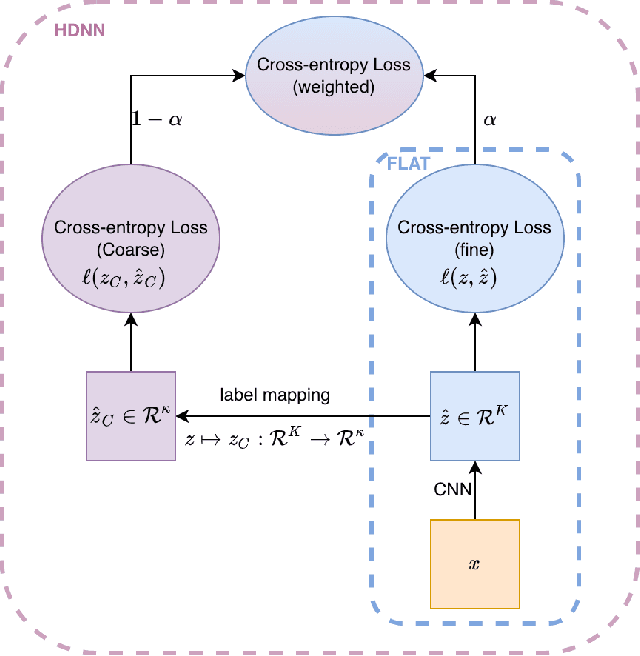
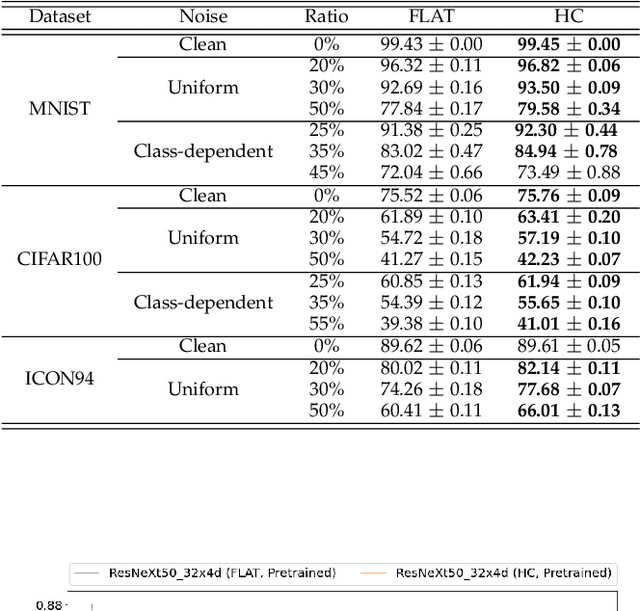
Deep neural networks are susceptible to label noise. Existing methods to improve robustness, such as meta-learning and regularization, usually require significant change to the network architecture or careful tuning of the optimization procedure. In this work, we propose a simple hierarchical approach that incorporates a label hierarchy when training the deep learning models. Our approach requires no change of the network architecture or the optimization procedure. We investigate our hierarchical network through a wide range of simulated and real datasets and various label noise types. Our hierarchical approach improves upon regular deep neural networks in learning with label noise. Combining our hierarchical approach with pre-trained models achieves state-of-the-art performance in real-world noisy datasets.

On identifying unobserved heterogeneity in stochastic blockmodel graphs with vertex covariates

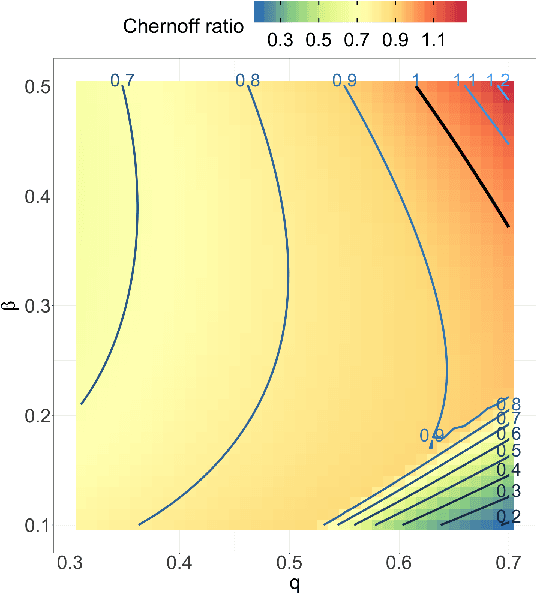
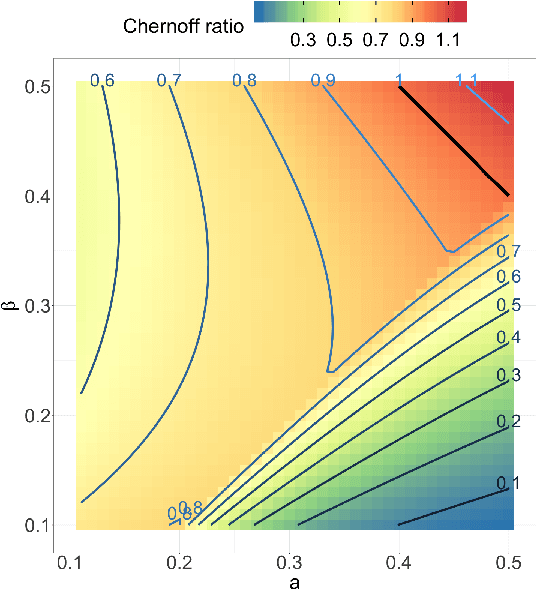
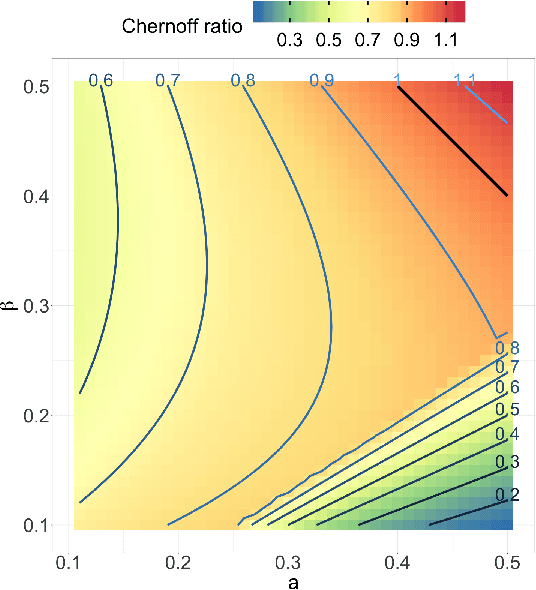
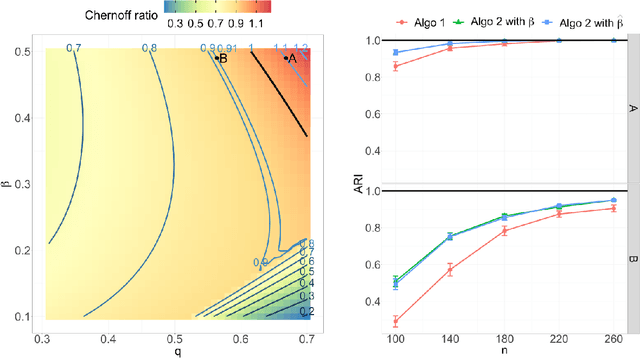
Both observed and unobserved vertex heterogeneity can influence block structure in graphs. To assess these effects on block recovery, we present a comparative analysis of two model-based spectral algorithms for clustering vertices in stochastic blockmodel graphs with vertex covariates. The first algorithm directly estimates the induced block assignments by investigating the estimated block connectivity probability matrix including the vertex covariate effect. The second algorithm estimates the vertex covariate effect and then estimates the induced block assignments after accounting for this effect. We employ Chernoff information to analytically compare the algorithms' performance and derive the Chernoff ratio formula for some special models of interest. Analytic results and simulations suggest that, in general, the second algorithm is preferred: we can better estimate the induced block assignments by first estimating the vertex covariate effect. In addition, real data experiments on a diffusion MRI connectome data set indicate that the second algorithm has the advantages of revealing underlying block structure and taking observed vertex heterogeneity into account in real applications. Our findings emphasize the importance of distinguishing between observed and unobserved factors that can affect block structure in graphs.