Understanding Input Selectivity in Mamba: Impact on Approximation Power, Memorization, and Associative Recall Capacity

State-Space Models (SSMs), and particularly Mamba, have recently emerged as a promising alternative to Transformers. Mamba introduces input selectivity to its SSM layer (S6) and incorporates convolution and gating into its block definition. While these modifications do improve Mamba's performance over its SSM predecessors, it remains largely unclear how Mamba leverages the additional functionalities provided by input selectivity, and how these interact with the other operations in the Mamba architecture. In this work, we demystify the role of input selectivity in Mamba, investigating its impact on function approximation power, long-term memorization, and associative recall capabilities. In particular: (i) we prove that the S6 layer of Mamba can represent projections onto Haar wavelets, providing an edge over its Diagonal SSM (S4D) predecessor in approximating discontinuous functions commonly arising in practice; (ii) we show how the S6 layer can dynamically counteract memory decay; (iii) we provide analytical solutions to the MQAR associative recall task using the Mamba architecture with different mixers -- Mamba, Mamba-2, and S4D. We demonstrate the tightness of our theoretical constructions with empirical results on concrete tasks. Our findings offer a mechanistic understanding of Mamba and reveal opportunities for improvement.

CAO-RONet: A Robust 4D Radar Odometry with Exploring More Information from Low-Quality Points

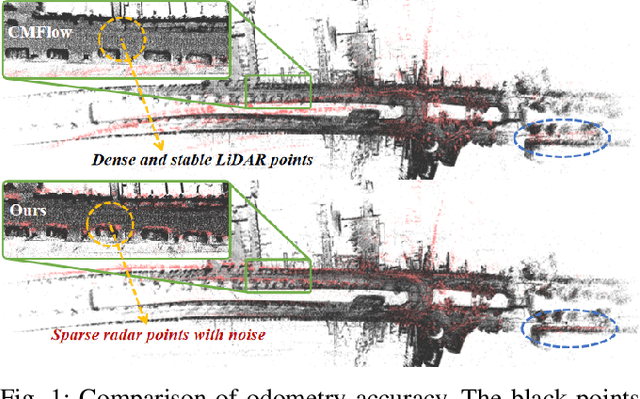
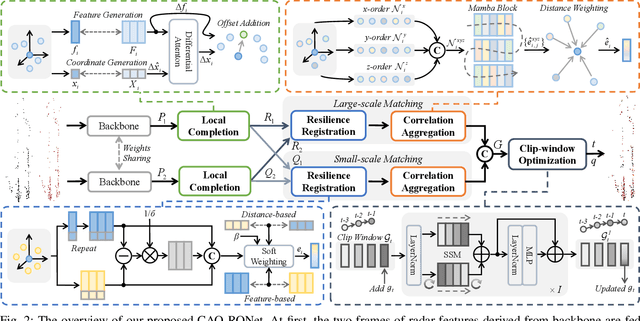
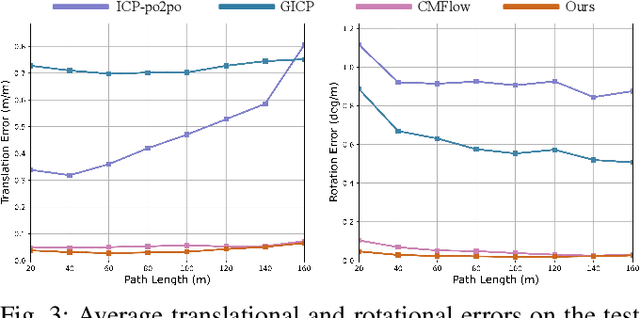
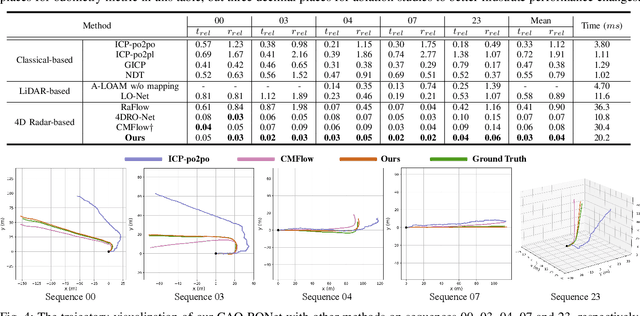
Recently, 4D millimetre-wave radar exhibits more stable perception ability than LiDAR and camera under adverse conditions (e.g. rain and fog). However, low-quality radar points hinder its application, especially the odometry task that requires a dense and accurate matching. To fully explore the potential of 4D radar, we introduce a learning-based odometry framework, enabling robust ego-motion estimation from finite and uncertain geometry information. First, for sparse radar points, we propose a local completion to supplement missing structures and provide denser guideline for aligning two frames. Then, a context-aware association with a hierarchical structure flexibly matches points of different scales aided by feature similarity, and improves local matching consistency through correlation balancing. Finally, we present a window-based optimizer that uses historical priors to establish a coupling state estimation and correct errors of inter-frame matching. The superiority of our algorithm is confirmed on View-of-Delft dataset, achieving around a 50% performance improvement over previous approaches and delivering accuracy on par with LiDAR odometry. Our code will be available.

Learning functions on symmetric matrices and point clouds via lightweight invariant features

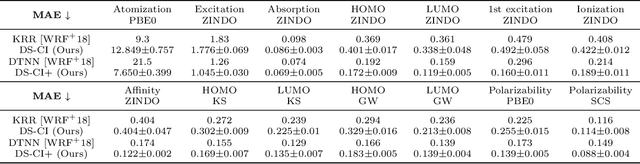
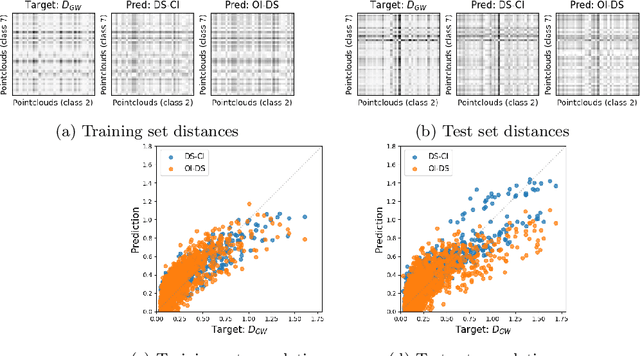
In this work, we present a mathematical formulation for machine learning of (1) functions on symmetric matrices that are invariant with respect to the action of permutations by conjugation, and (2) functions on point clouds that are invariant with respect to rotations, reflections, and permutations of the points. To achieve this, we construct $O(n^2)$ invariant features derived from generators for the field of rational functions on $n\times n$ symmetric matrices that are invariant under joint permutations of rows and columns. We show that these invariant features can separate all distinct orbits of symmetric matrices except for a measure zero set; such features can be used to universally approximate invariant functions on almost all weighted graphs. For point clouds in a fixed dimension, we prove that the number of invariant features can be reduced, generically without losing expressivity, to $O(n)$, where $n$ is the number of points. We combine these invariant features with DeepSets to learn functions on symmetric matrices and point clouds with varying sizes. We empirically demonstrate the feasibility of our approach on molecule property regression and point cloud distance prediction.

Approximately Equivariant Graph Networks

Graph neural networks (GNNs) are commonly described as being permutation equivariant with respect to node relabeling in the graph. This symmetry of GNNs is often compared to the translation equivariance symmetry of Euclidean convolution neural networks (CNNs). However, these two symmetries are fundamentally different: The translation equivariance of CNNs corresponds to symmetries of the fixed domain acting on the image signal (sometimes known as active symmetries), whereas in GNNs any permutation acts on both the graph signals and the graph domain (sometimes described as passive symmetries). In this work, we focus on the active symmetries of GNNs, by considering a learning setting where signals are supported on a fixed graph. In this case, the natural symmetries of GNNs are the automorphisms of the graph. Since real-world graphs tend to be asymmetric, we relax the notion of symmetries by formalizing approximate symmetries via graph coarsening. We present a bias-variance formula that quantifies the tradeoff between the loss in expressivity and the gain in the regularity of the learned estimator, depending on the chosen symmetry group. To illustrate our approach, we conduct extensive experiments on image inpainting, traffic flow prediction, and human pose estimation with different choices of symmetries. We show theoretically and empirically that the best generalization performance can be achieved by choosing a suitably larger group than the graph automorphism group, but smaller than the full permutation group.

Fine-grained Expressivity of Graph Neural Networks

Numerous recent works have analyzed the expressive power of message-passing graph neural networks (MPNNs), primarily utilizing combinatorial techniques such as the $1$-dimensional Weisfeiler-Leman test ($1$-WL) for the graph isomorphism problem. However, the graph isomorphism objective is inherently binary, not giving insights into the degree of similarity between two given graphs. This work resolves this issue by considering continuous extensions of both $1$-WL and MPNNs to graphons. Concretely, we show that the continuous variant of $1$-WL delivers an accurate topological characterization of the expressive power of MPNNs on graphons, revealing which graphs these networks can distinguish and the level of difficulty in separating them. We identify the finest topology where MPNNs separate points and prove a universal approximation theorem. Consequently, we provide a theoretical framework for graph and graphon similarity combining various topological variants of classical characterizations of the $1$-WL. In particular, we characterize the expressive power of MPNNs in terms of the tree distance, which is a graph distance based on the concepts of fractional isomorphisms, and substructure counts via tree homomorphisms, showing that these concepts have the same expressive power as the $1$-WL and MPNNs on graphons. Empirically, we validate our theoretical findings by showing that randomly initialized MPNNs, without training, exhibit competitive performance compared to their trained counterparts. Moreover, we evaluate different MPNN architectures based on their ability to preserve graph distances, highlighting the significance of our continuous $1$-WL test in understanding MPNNs' expressivity.

Graph Neural Networks for Community Detection on Sparse Graphs

Spectral methods provide consistent estimators for community detection in dense graphs. However, their performance deteriorates as the graphs become sparser. In this work we consider a random graph model that can produce graphs at different levels of sparsity, and we show that graph neural networks can outperform spectral methods on sparse graphs. We illustrate the results with numerical examples in both synthetic and real graphs.

Deep Learning is Provably Robust to Symmetric Label Noise

Deep neural networks (DNNs) are capable of perfectly fitting the training data, including memorizing noisy data. It is commonly believed that memorization hurts generalization. Therefore, many recent works propose mitigation strategies to avoid noisy data or correct memorization. In this work, we step back and ask the question: Can deep learning be robust against massive label noise without any mitigation? We provide an affirmative answer for the case of symmetric label noise: We find that certain DNNs, including under-parameterized and over-parameterized models, can tolerate massive symmetric label noise up to the information-theoretic threshold. By appealing to classical statistical theory and universal consistency of DNNs, we prove that for multiclass classification, $L_1$-consistent DNN classifiers trained under symmetric label noise can achieve Bayes optimality asymptotically if the label noise probability is less than $\frac{K-1}{K}$, where $K \ge 2$ is the number of classes. Our results show that for symmetric label noise, no mitigation is necessary for $L_1$-consistent estimators. We conjecture that for general label noise, mitigation strategies that make use of the noisy data will outperform those that ignore the noisy data.

From Local to Global: Spectral-Inspired Graph Neural Networks

Graph Neural Networks (GNNs) are powerful deep learning methods for Non-Euclidean data. Popular GNNs are message-passing algorithms (MPNNs) that aggregate and combine signals in a local graph neighborhood. However, shallow MPNNs tend to miss long-range signals and perform poorly on some heterophilous graphs, while deep MPNNs can suffer from issues like over-smoothing or over-squashing. To mitigate such issues, existing works typically borrow normalization techniques from training neural networks on Euclidean data or modify the graph structures. Yet these approaches are not well-understood theoretically and could increase the overall computational complexity. In this work, we draw inspirations from spectral graph embedding and propose $\texttt{PowerEmbed}$ -- a simple layer-wise normalization technique to boost MPNNs. We show $\texttt{PowerEmbed}$ can provably express the top-$k$ leading eigenvectors of the graph operator, which prevents over-smoothing and is agnostic to the graph topology; meanwhile, it produces a list of representations ranging from local features to global signals, which avoids over-squashing. We apply $\texttt{PowerEmbed}$ in a wide range of simulated and real graphs and demonstrate its competitive performance, particularly for heterophilous graphs.

Endowing Language Models with Multimodal Knowledge Graph Representations

We propose a method to make natural language understanding models more parameter efficient by storing knowledge in an external knowledge graph (KG) and retrieving from this KG using a dense index. Given (possibly multilingual) downstream task data, e.g., sentences in German, we retrieve entities from the KG and use their multimodal representations to improve downstream task performance. We use the recently released VisualSem KG as our external knowledge repository, which covers a subset of Wikipedia and WordNet entities, and compare a mix of tuple-based and graph-based algorithms to learn entity and relation representations that are grounded on the KG multimodal information. We demonstrate the usefulness of the learned entity representations on two downstream tasks, and show improved performance on the multilingual named entity recognition task by $0.3\%$--$0.7\%$ F1, while we achieve up to $2.5\%$ improvement in accuracy on the visual sense disambiguation task. All our code and data are available in: \url{https://github.com/iacercalixto/visualsem-kg}.

Deep Learning with Label Noise: A Hierarchical Approach

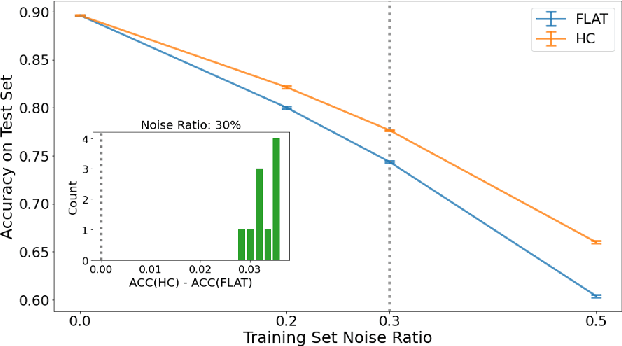
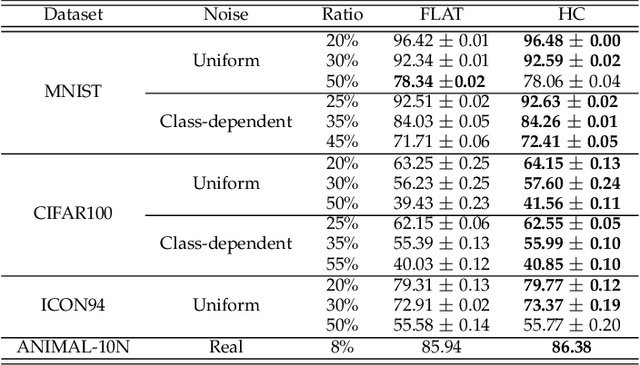
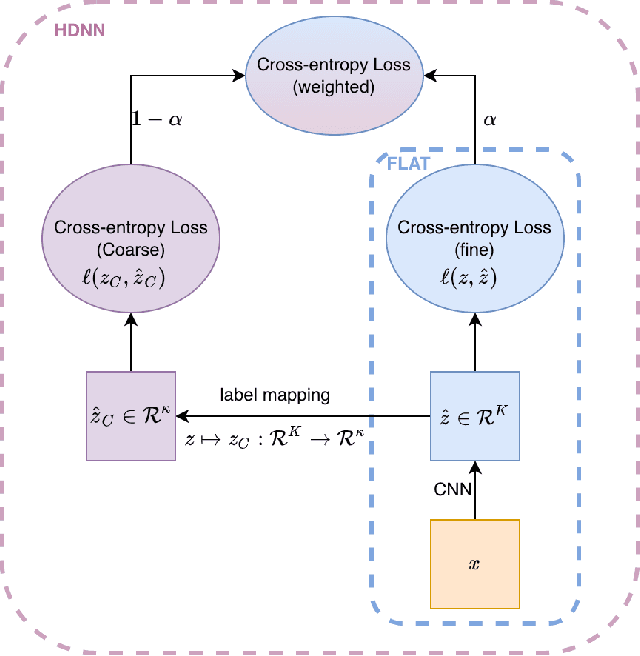
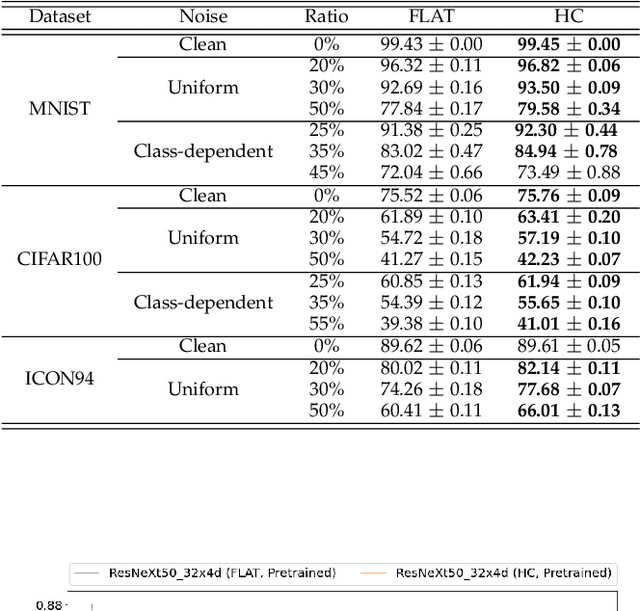
Deep neural networks are susceptible to label noise. Existing methods to improve robustness, such as meta-learning and regularization, usually require significant change to the network architecture or careful tuning of the optimization procedure. In this work, we propose a simple hierarchical approach that incorporates a label hierarchy when training the deep learning models. Our approach requires no change of the network architecture or the optimization procedure. We investigate our hierarchical network through a wide range of simulated and real datasets and various label noise types. Our hierarchical approach improves upon regular deep neural networks in learning with label noise. Combining our hierarchical approach with pre-trained models achieves state-of-the-art performance in real-world noisy datasets.