Optimizing the Induced Correlation in Omnibus Joint Graph Embeddings

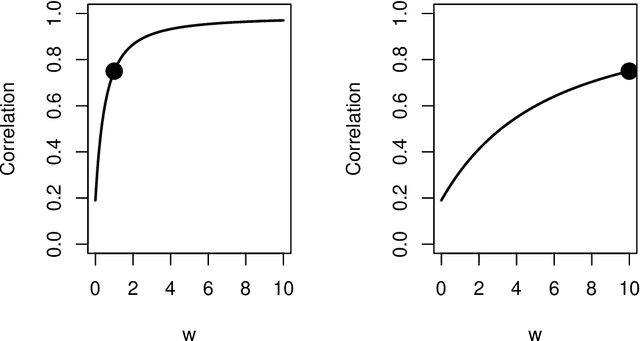
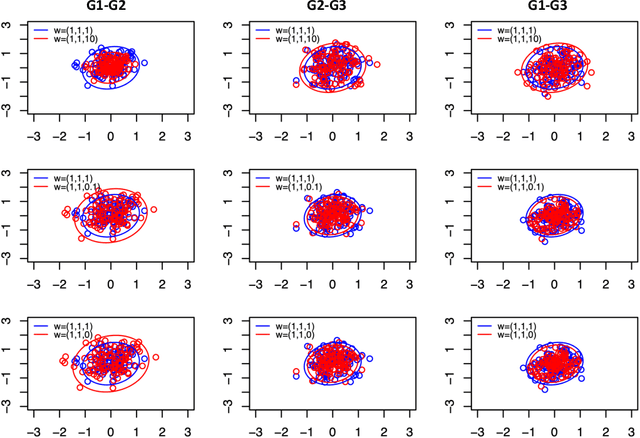
Theoretical and empirical evidence suggests that joint graph embedding algorithms induce correlation across the networks in the embedding space. In the Omnibus joint graph embedding framework, previous results explicitly delineated the dual effects of the algorithm-induced and model-inherent correlations on the correlation across the embedded networks. Accounting for and mitigating the algorithm-induced correlation is key to subsequent inference, as sub-optimal Omnibus matrix constructions have been demonstrated to lead to loss in inference fidelity. This work presents the first efforts to automate the Omnibus construction in order to address two key questions in this joint embedding framework: the correlation-to-OMNI problem and the flat correlation problem. In the flat correlation problem, we seek to understand the minimum algorithm-induced flat correlation (i.e., the same across all graph pairs) produced by a generalized Omnibus embedding. Working in a subspace of the fully general Omnibus matrices, we prove both a lower bound for this flat correlation and that the classical Omnibus construction induces the maximal flat correlation. In the correlation-to-OMNI problem, we present an algorithm -- named corr2Omni -- that, from a given matrix of estimated pairwise graph correlations, estimates the matrix of generalized Omnibus weights that induces optimal correlation in the embedding space. Moreover, in both simulated and real data settings, we demonstrate the increased effectiveness of our corr2Omni algorithm versus the classical Omnibus construction.

The Importance of Being Correlated: Implications of Dependence in Joint Spectral Inference across Multiple Networks

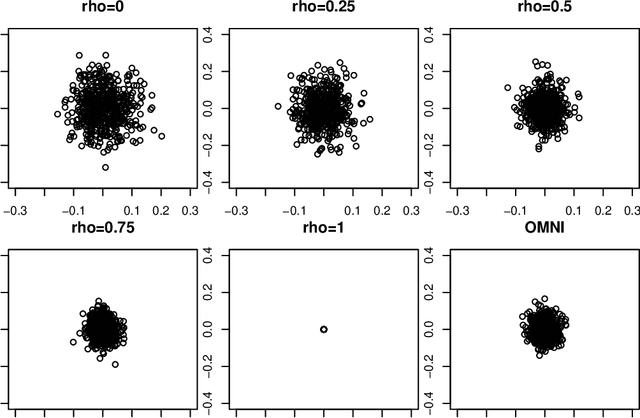
Spectral inference on multiple networks is a rapidly-developing subfield of graph statistics. Recent work has demonstrated that joint, or simultaneous, spectral embedding of multiple independent network realizations can deliver more accurate estimation than individual spectral decompositions of those same networks. Little attention has been paid, however, to the network correlation that such joint embedding procedures necessarily induce. In this paper, we present a detailed analysis of induced correlation in a {\em generalized omnibus} embedding for multiple networks. We show that our embedding procedure is flexible and robust, and, moreover, we prove a central limit theorem for this embedding and explicitly compute the limiting covariance. We examine how this covariance can impact inference in a network time series, and we construct an appropriately calibrated omnibus embedding that can detect changes in real biological networks that previous embedding procedures could not discern. Our analysis confirms that the effect of induced correlation can be both subtle and transformative, with import in theory and practice.