Comparing analytic and data-driven approaches to parameter identifiability: A power systems case study

Parameter identifiability refers to the capability of accurately inferring the parameter values of a model from its observations (data). Traditional analysis methods exploit analytical properties of the closed form model, in particular sensitivity analysis, to quantify the response of the model predictions to variations in parameters. Techniques developed to analyze data, specifically manifold learning methods, have the potential to complement, and even extend the scope of the traditional analytical approaches. We report on a study comparing and contrasting analytical and data-driven approaches to quantify parameter identifiability and, importantly, perform parameter reduction tasks. We use the infinite bus synchronous generator model, a well-understood model from the power systems domain, as our benchmark problem. Our traditional analysis methods use the Fisher Information Matrix to quantify parameter identifiability analysis, and the Manifold Boundary Approximation Method to perform parameter reduction. We compare these results to those arrived at through data-driven manifold learning schemes: Output - Diffusion Maps and Geometric Harmonics. For our test case, we find that the two suites of tools (analytical when a model is explicitly available, as well as data-driven when the model is lacking and only measurement data are available) give (correct) comparable results; these results are also in agreement with traditional analysis based on singular perturbation theory. We then discuss the prospects of using data-driven methods for such model analysis.

An information-matching approach to optimal experimental design and active learning

The efficacy of mathematical models heavily depends on the quality of the training data, yet collecting sufficient data is often expensive and challenging. Many modeling applications require inferring parameters only as a means to predict other quantities of interest (QoI). Because models often contain many unidentifiable (sloppy) parameters, QoIs often depend on a relatively small number of parameter combinations. Therefore, we introduce an information-matching criterion based on the Fisher Information Matrix to select the most informative training data from a candidate pool. This method ensures that the selected data contain sufficient information to learn only those parameters that are needed to constrain downstream QoIs. It is formulated as a convex optimization problem, making it scalable to large models and datasets. We demonstrate the effectiveness of this approach across various modeling problems in diverse scientific fields, including power systems and underwater acoustics. Finally, we use information-matching as a query function within an Active Learning loop for material science applications. In all these applications, we find that a relatively small set of optimal training data can provide the necessary information for achieving precise predictions. These results are encouraging for diverse future applications, particularly active learning in large machine learning models.

Aliasing and Label-Independent Decomposition of Risk: Beyond the bias-variance trade-off

A central problem in data science is to use potentially noisy samples of an unknown function to predict function values for unseen inputs. In classical statistics, the predictive error is understood as a trade-off between the bias and the variance that balances model simplicity with its ability to fit complex functions. However, over-parameterized models exhibit counter-intuitive behaviors, such as "double descent" in which models of increasing complexity exhibit decreasing generalization error. We introduce an alternative paradigm called the generalized aliasing decomposition. We explain the asymptotically small error of complex models as a systematic "de-aliasing" that occurs in the over-parameterized regime. In the limit of large models, the contribution due to aliasing vanishes, leaving an expression for the asymptotic total error we call the invertibility failure of very large models on few training points. Because the generalized aliasing decomposition can be explicitly calculated from the relationship between model class and samples without seeing any data labels, it can answer questions related to experimental design and model selection before collecting data or performing experiments. We demonstrate this approach using several examples, including classical regression problems and a cluster expansion model used in materials science.

The Training Process of Many Deep Networks Explores the Same Low-Dimensional Manifold

We develop information-geometric techniques to analyze the trajectories of the predictions of deep networks during training. By examining the underlying high-dimensional probabilistic models, we reveal that the training process explores an effectively low-dimensional manifold. Networks with a wide range of architectures, sizes, trained using different optimization methods, regularization techniques, data augmentation techniques, and weight initializations lie on the same manifold in the prediction space. We study the details of this manifold to find that networks with different architectures follow distinguishable trajectories but other factors have a minimal influence; larger networks train along a similar manifold as that of smaller networks, just faster; and networks initialized at very different parts of the prediction space converge to the solution along a similar manifold.

Maximizing the information learned from finite data selects a simple model

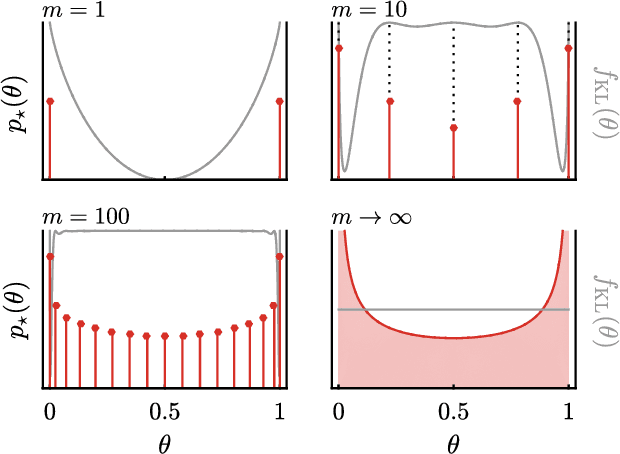
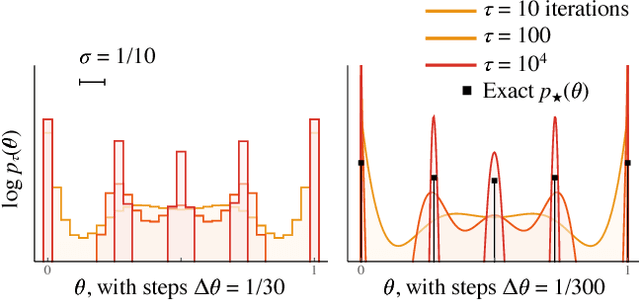
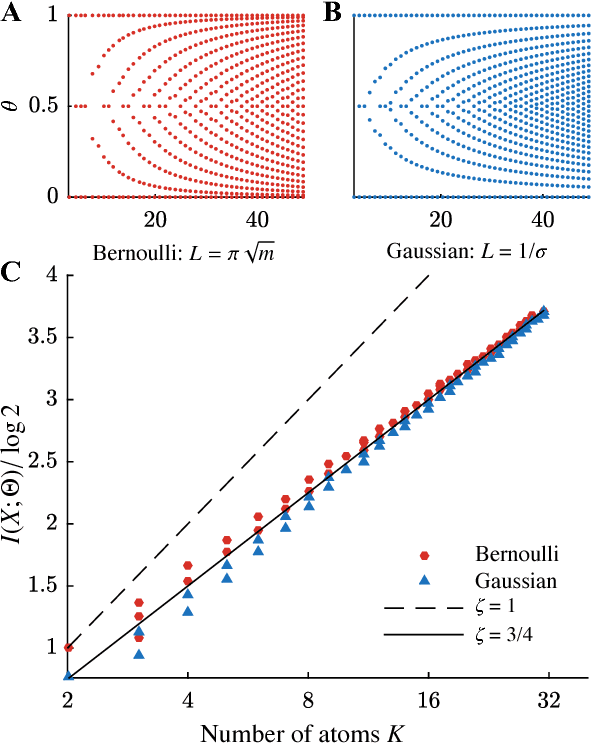
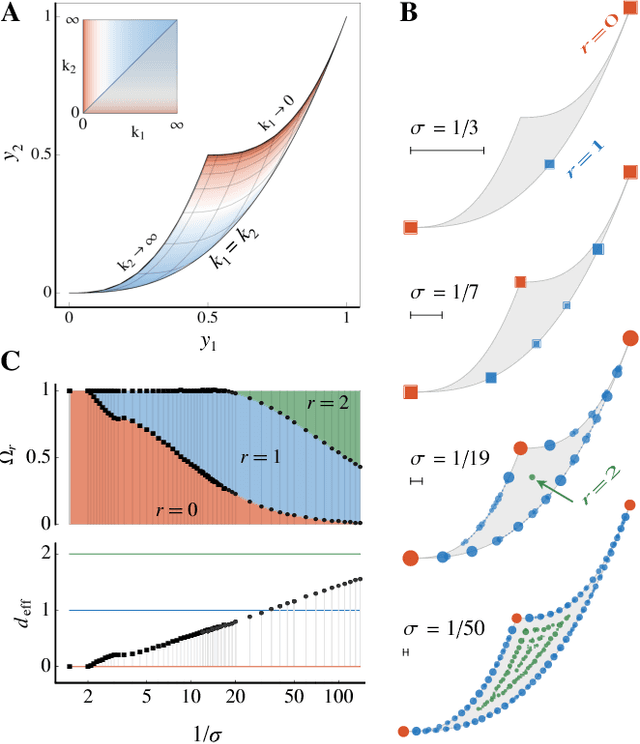
We use the language of uninformative Bayesian prior choice to study the selection of appropriately simple effective models. We advocate for the prior which maximizes the mutual information between parameters and predictions, learning as much as possible from limited data. When many parameters are poorly constrained by the available data, we find that this prior puts weight only on boundaries of the parameter manifold. Thus it selects a lower-dimensional effective theory in a principled way, ignoring irrelevant parameter directions. In the limit where there is sufficient data to tightly constrain any number of parameters, this reduces to Jeffreys prior. But we argue that this limit is pathological when applied to the hyper-ribbon parameter manifolds generic in science, because it leads to dramatic dependence on effects invisible to experiment.