A probabilistic foundation model for crystal structure denoising, phase classification, and order parameters

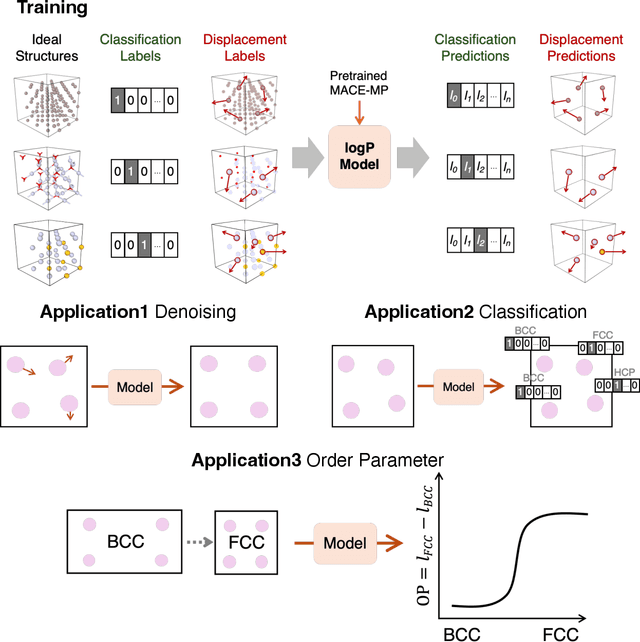
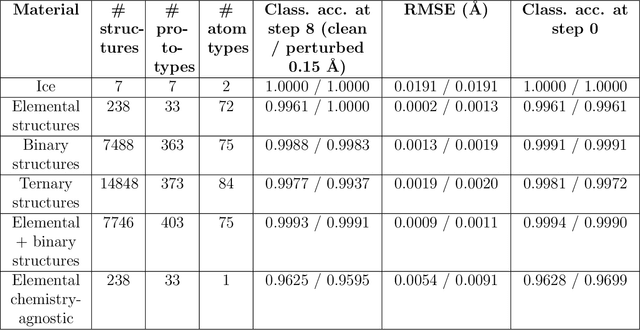
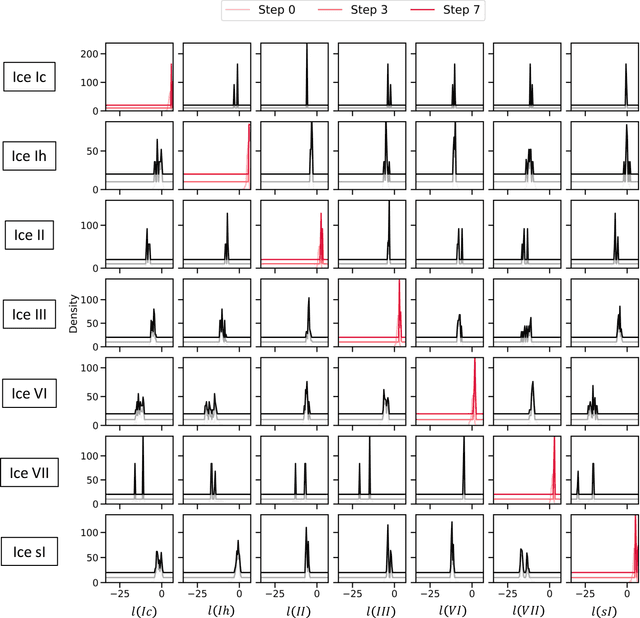
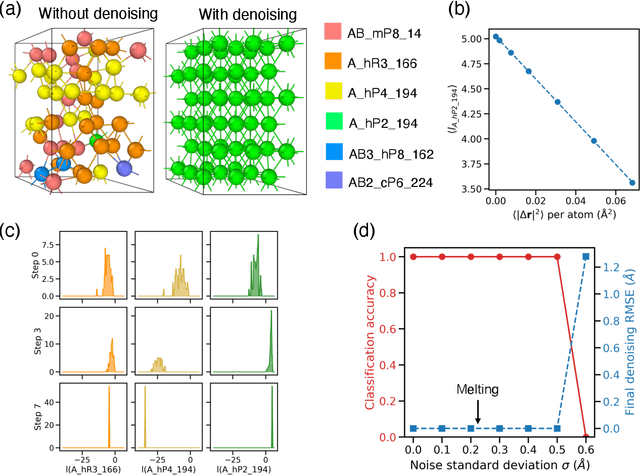
Atomistic simulations generate large volumes of noisy structural data, but extracting phase labels, order parameters (OPs), and defect information in a way that is universal, robust, and interpretable remains challenging. Existing tools such as PTM and CNA are restricted to a small set of hand-crafted lattices (e.g.\ FCC/BCC/HCP), degrade under strong thermal disorder or defects, and produce hard, template-based labels without per-atom probability or confidence scores. Here we introduce a log-probability foundation model that unifies denoising, phase classification, and OP extraction within a single probabilistic framework. We reuse the MACE-MP foundation interatomic potential on crystal structures mapped to AFLOW prototypes, training it to predict per-atom, per-phase logits $l$ and to aggregate them into a global log-density $\log \hat{P}_θ(\boldsymbol{r})$ whose gradient defines a conservative score field. Denoising corresponds to gradient ascent on this learned log-density, phase labels follow from $\arg\max_c l_{ac}$, and the $l$ values act as continuous, defect-sensitive and interpretable OPs quantifying the Euclidean distance to ideal phases. We demonstrate universality across hundreds of prototypes, robustness under strong thermal and defect-induced disorder, and accurate treatment of complex systems such as ice polymorphs, ice--water interfaces, and shock-compressed Ti.

Maximizing Efficiency of Dataset Compression for Machine Learning Potentials With Information Theory

Machine learning interatomic potentials (MLIPs) balance high accuracy and lower costs compared to density functional theory calculations, but their performance often depends on the size and diversity of training datasets. Large datasets improve model accuracy and generalization but are computationally expensive to produce and train on, while smaller datasets risk discarding rare but important atomic environments and compromising MLIP accuracy/reliability. Here, we develop an information-theoretical framework to quantify the efficiency of dataset compression methods and propose an algorithm that maximizes this efficiency. By framing atomistic dataset compression as an instance of the minimum set cover (MSC) problem over atom-centered environments, our method identifies the smallest subset of structures that contains as much information as possible from the original dataset while pruning redundant information. The approach is extensively demonstrated on the GAP-20 and TM23 datasets, and validated on 64 varied datasets from the ColabFit repository. Across all cases, MSC consistently retains outliers, preserves dataset diversity, and reproduces the long-tail distributions of forces even at high compression rates, outperforming other subsampling methods. Furthermore, MLIPs trained on MSC-compressed datasets exhibit reduced error for out-of-distribution data even in low-data regimes. We explain these results using an outlier analysis and show that such quantitative conclusions could not be achieved with conventional dimensionality reduction methods. The algorithm is implemented in the open-source QUESTS package and can be used for several tasks in atomistic modeling, from data subsampling, outlier detection, and training improved MLIPs at a lower cost.

Unsupervised Atomic Data Mining via Multi-Kernel Graph Autoencoders for Machine Learning Force Fields

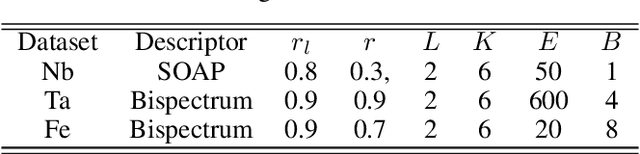
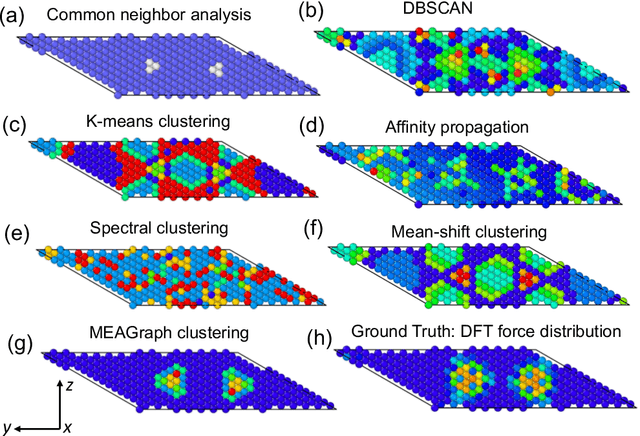
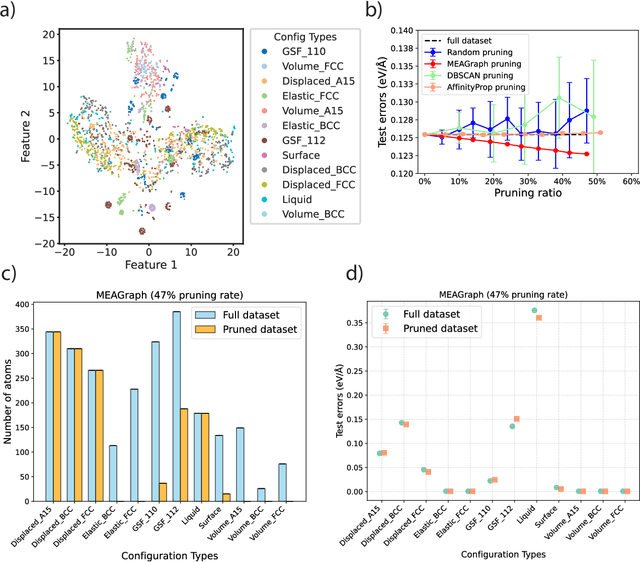
Constructing a chemically diverse dataset while avoiding sampling bias is critical to training efficient and generalizable force fields. However, in computational chemistry and materials science, many common dataset generation techniques are prone to oversampling regions of the potential energy surface. Furthermore, these regions can be difficult to identify and isolate from each other or may not align well with human intuition, making it challenging to systematically remove bias in the dataset. While traditional clustering and pruning (down-sampling) approaches can be useful for this, they can often lead to information loss or a failure to properly identify distinct regions of the potential energy surface due to difficulties associated with the high dimensionality of atomic descriptors. In this work, we introduce the Multi-kernel Edge Attention-based Graph Autoencoder (MEAGraph) model, an unsupervised approach for analyzing atomic datasets. MEAGraph combines multiple linear kernel transformations with attention-based message passing to capture geometric sensitivity and enable effective dataset pruning without relying on labels or extensive training. Demonstrated applications on niobium, tantalum, and iron datasets show that MEAGraph efficiently groups similar atomic environments, allowing for the use of basic pruning techniques for removing sampling bias. This approach provides an effective method for representation learning and clustering that can be used for data analysis, outlier detection, and dataset optimization.

Composable and adaptive design of machine learning interatomic potentials guided by Fisher-information analysis

An adaptive physics-informed model design strategy for machine-learning interatomic potentials (MLIPs) is proposed. This strategy follows an iterative reconfiguration of composite models from single-term models, followed by a unified training procedure. A model evaluation method based on the Fisher information matrix (FIM) and multiple-property error metrics is proposed to guide model reconfiguration and hyperparameter optimization. Combining the model reconfiguration and the model evaluation subroutines, we provide an adaptive MLIP design strategy that balances flexibility and extensibility. In a case study of designing models against a structurally diverse niobium dataset, we managed to obtain an optimal configuration with 75 parameters generated by our framework that achieved a force RMSE of 0.172 eV/{\AA} and an energy RMSE of 0.013 eV/atom.

An information-matching approach to optimal experimental design and active learning

The efficacy of mathematical models heavily depends on the quality of the training data, yet collecting sufficient data is often expensive and challenging. Many modeling applications require inferring parameters only as a means to predict other quantities of interest (QoI). Because models often contain many unidentifiable (sloppy) parameters, QoIs often depend on a relatively small number of parameter combinations. Therefore, we introduce an information-matching criterion based on the Fisher Information Matrix to select the most informative training data from a candidate pool. This method ensures that the selected data contain sufficient information to learn only those parameters that are needed to constrain downstream QoIs. It is formulated as a convex optimization problem, making it scalable to large models and datasets. We demonstrate the effectiveness of this approach across various modeling problems in diverse scientific fields, including power systems and underwater acoustics. Finally, we use information-matching as a query function within an Active Learning loop for material science applications. In all these applications, we find that a relatively small set of optimal training data can provide the necessary information for achieving precise predictions. These results are encouraging for diverse future applications, particularly active learning in large machine learning models.

Grand canonical generative diffusion model for crystalline phases and grain boundaries

The diffusion model has emerged as a powerful tool for generating atomic structures for materials science. This work calls attention to the deficiency of current particle-based diffusion models, which represent atoms as a point cloud, in generating even the simplest ordered crystalline structures. The problem is attributed to particles being trapped in local minima during the score-driven simulated annealing of the diffusion process, similar to the physical process of force-driven simulated annealing. We develop a solution, the grand canonical diffusion model, which adopts an alternative voxel-based representation with continuous rather than fixed number of particles. The method is applied towards generation of several common crystalline phases as well as the technologically important and challenging problem of grain boundary structures.

Information theory unifies atomistic machine learning, uncertainty quantification, and materials thermodynamics

An accurate description of information is relevant for a range of problems in atomistic modeling, such as sampling methods, detecting rare events, analyzing datasets, or performing uncertainty quantification (UQ) in machine learning (ML)-driven simulations. Although individual methods have been proposed for each of these tasks, they lack a common theoretical background integrating their solutions. Here, we introduce an information theoretical framework that unifies predictions of phase transformations, kinetic events, dataset optimality, and model-free UQ from atomistic simulations, thus bridging materials modeling, ML, and statistical mechanics. We first demonstrate that, for a proposed representation, the information entropy of a distribution of atom-centered environments is a surrogate value for thermodynamic entropy. Using molecular dynamics (MD) simulations, we show that information entropy differences from trajectories can be used to build phase diagrams, identify rare events, and recover classical theories of nucleation. Building on these results, we use this general concept of entropy to quantify information in datasets for ML interatomic potentials (IPs), informing compression, explaining trends in testing errors, and evaluating the efficiency of active learning strategies. Finally, we propose a model-free UQ method for MLIPs using information entropy, showing it reliably detects extrapolation regimes, scales to millions of atoms, and goes beyond model errors. This method is made available as the package QUESTS: Quick Uncertainty and Entropy via STructural Similarity, providing a new unifying theory for data-driven atomistic modeling and combining efforts in ML, first-principles thermodynamics, and simulations.

LTAU-FF: Loss Trajectory Analysis for Uncertainty in Atomistic Force Fields

Model ensembles are simple and effective tools for estimating the prediction uncertainty of deep learning atomistic force fields. Despite this, widespread adoption of ensemble-based uncertainty quantification (UQ) techniques is limited by the high computational costs incurred by ensembles during both training and inference. In this work we leverage the cumulative distribution functions (CDFs) of per-sample errors obtained over the course of training to efficiently represent the model ensemble, and couple them with a distance-based similarity search in the model latent space. Using these tools, we develop a simple UQ metric (which we call LTAU) that leverages the strengths of ensemble-based techniques without requiring the evaluation of multiple models during either training or inference. As an initial test, we apply our method towards estimating the epistemic uncertainty in atomistic force fields (LTAU-FF) and demonstrate that it can be easily calibrated to accurately predict test errors on multiple datasets from the literature. We then illustrate the utility of LTAU-FF in two practical applications: 1) tuning the training-validation gap for an example dataset, and 2) predicting errors in relaxation trajectories on the OC20 IS2RS task. Though in this work we focus on the use of LTAU with deep learning atomistic force fields, we emphasize that it can be readily applied to any regression task, or any ensemble-generation technique, to provide a reliable and easy-to-implement UQ metric.