Joshua A. Vita
Unsupervised Atomic Data Mining via Multi-Kernel Graph Autoencoders for Machine Learning Force Fields
Sep 15, 2025
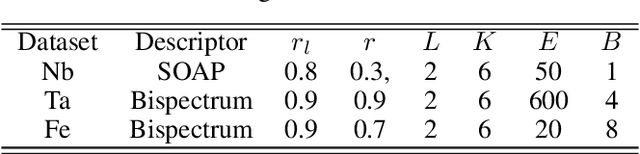
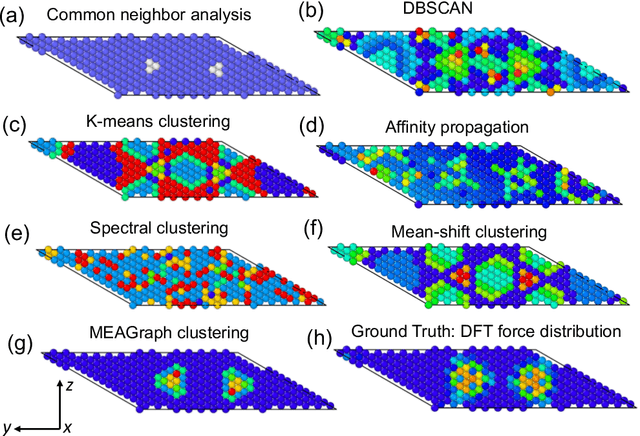
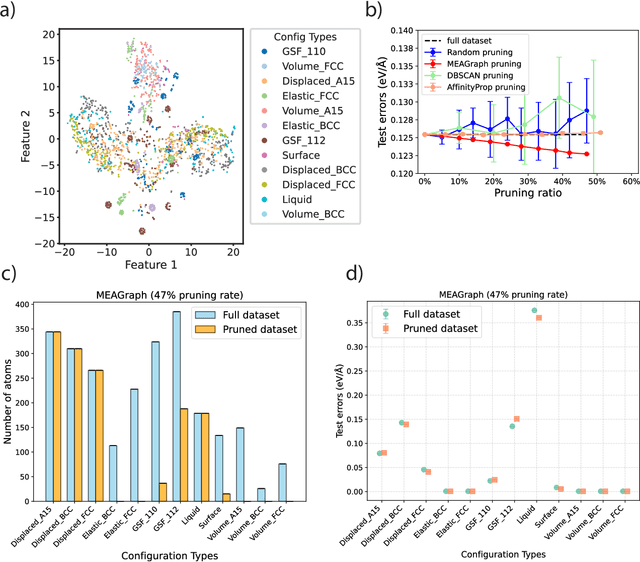
Abstract:Constructing a chemically diverse dataset while avoiding sampling bias is critical to training efficient and generalizable force fields. However, in computational chemistry and materials science, many common dataset generation techniques are prone to oversampling regions of the potential energy surface. Furthermore, these regions can be difficult to identify and isolate from each other or may not align well with human intuition, making it challenging to systematically remove bias in the dataset. While traditional clustering and pruning (down-sampling) approaches can be useful for this, they can often lead to information loss or a failure to properly identify distinct regions of the potential energy surface due to difficulties associated with the high dimensionality of atomic descriptors. In this work, we introduce the Multi-kernel Edge Attention-based Graph Autoencoder (MEAGraph) model, an unsupervised approach for analyzing atomic datasets. MEAGraph combines multiple linear kernel transformations with attention-based message passing to capture geometric sensitivity and enable effective dataset pruning without relying on labels or extensive training. Demonstrated applications on niobium, tantalum, and iron datasets show that MEAGraph efficiently groups similar atomic environments, allowing for the use of basic pruning techniques for removing sampling bias. This approach provides an effective method for representation learning and clustering that can be used for data analysis, outlier detection, and dataset optimization.
LTAU-FF: Loss Trajectory Analysis for Uncertainty in Atomistic Force Fields
Feb 01, 2024Abstract:Model ensembles are simple and effective tools for estimating the prediction uncertainty of deep learning atomistic force fields. Despite this, widespread adoption of ensemble-based uncertainty quantification (UQ) techniques is limited by the high computational costs incurred by ensembles during both training and inference. In this work we leverage the cumulative distribution functions (CDFs) of per-sample errors obtained over the course of training to efficiently represent the model ensemble, and couple them with a distance-based similarity search in the model latent space. Using these tools, we develop a simple UQ metric (which we call LTAU) that leverages the strengths of ensemble-based techniques without requiring the evaluation of multiple models during either training or inference. As an initial test, we apply our method towards estimating the epistemic uncertainty in atomistic force fields (LTAU-FF) and demonstrate that it can be easily calibrated to accurately predict test errors on multiple datasets from the literature. We then illustrate the utility of LTAU-FF in two practical applications: 1) tuning the training-validation gap for an example dataset, and 2) predicting errors in relaxation trajectories on the OC20 IS2RS task. Though in this work we focus on the use of LTAU with deep learning atomistic force fields, we emphasize that it can be readily applied to any regression task, or any ensemble-generation technique, to provide a reliable and easy-to-implement UQ metric.
Spline-based neural network interatomic potentials: blending classical and machine learning models
Oct 04, 2023Abstract:While machine learning (ML) interatomic potentials (IPs) are able to achieve accuracies nearing the level of noise inherent in the first-principles data to which they are trained, it remains to be shown if their increased complexities are strictly necessary for constructing high-quality IPs. In this work, we introduce a new MLIP framework which blends the simplicity of spline-based MEAM (s-MEAM) potentials with the flexibility of a neural network (NN) architecture. The proposed framework, which we call the spline-based neural network potential (s-NNP), is a simplified version of the traditional NNP that can be used to describe complex datasets in a computationally efficient manner. We demonstrate how this framework can be used to probe the boundary between classical and ML IPs, highlighting the benefits of key architectural changes. Furthermore, we show that using spline filters for encoding atomic environments results in a readily interpreted embedding layer which can be coupled with modifications to the NN to incorporate expected physical behaviors and improve overall interpretability. Finally, we test the flexibility of the spline filters, observing that they can be shared across multiple chemical systems in order to provide a convenient reference point from which to begin performing cross-system analyses.
Data efficiency and extrapolation trends in neural network interatomic potentials
Feb 12, 2023Abstract:Over the last few years, key architectural advances have been proposed for neural network interatomic potentials (NNIPs), such as incorporating message-passing networks, equivariance, or many-body expansion terms. Although modern NNIP models exhibit nearly negligible differences in energy/forces errors, improvements in accuracy are still considered the main target when developing new NNIP architectures. In this work, we investigate how architectural choices influence the trainability and generalization error in NNIPs, revealing trends in extrapolation, data efficiency, and loss landscapes. First, we show that modern NNIP architectures recover the underlying potential energy surface (PES) of the training data even when trained to corrupted labels. Second, generalization metrics such as errors on high-temperature samples from the 3BPA dataset are demonstrated to follow a scaling relation for a variety of models. Thus, improvements in accuracy metrics may not bring independent information on the robust generalization of NNIPs. To circumvent this problem, we relate loss landscapes to model generalization across datasets. Using this probe, we explain why NNIPs with similar accuracy metrics exhibit different abilities to extrapolate and how training to forces improves the optimization landscape of a model. As an example, we show that MACE can predict PESes with reasonable error after being trained to as few as five data points, making it an example of a "few-shot" model for learning PESes. On the other hand, models with similar accuracy metrics such as NequIP show smaller ability to extrapolate in this extremely low-data regime. Our work provides a deep learning justification for the performance of many common NNIPs, and introduces tools beyond accuracy metrics that can be used to inform the development of next-generation models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge