Aliasing and Label-Independent Decomposition of Risk: Beyond the bias-variance trade-off

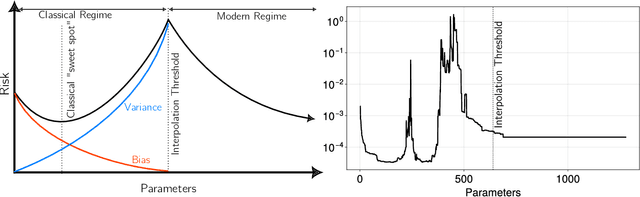
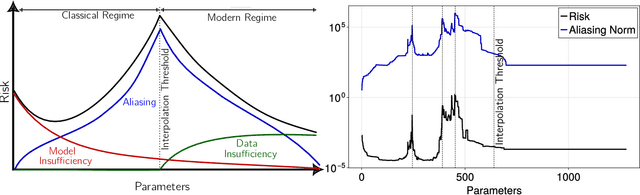
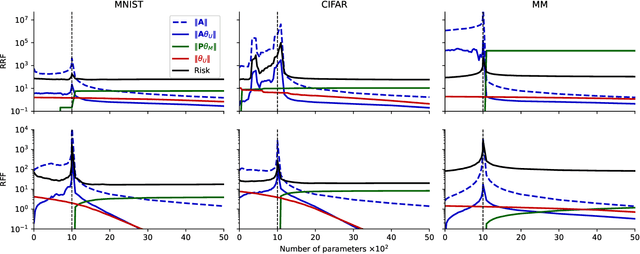
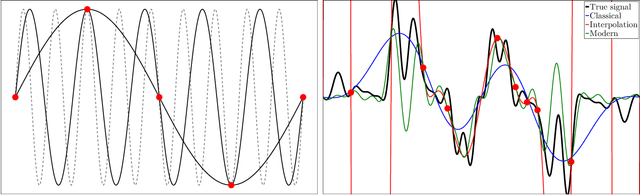
A central problem in data science is to use potentially noisy samples of an unknown function to predict function values for unseen inputs. In classical statistics, the predictive error is understood as a trade-off between the bias and the variance that balances model simplicity with its ability to fit complex functions. However, over-parameterized models exhibit counter-intuitive behaviors, such as "double descent" in which models of increasing complexity exhibit decreasing generalization error. We introduce an alternative paradigm called the generalized aliasing decomposition. We explain the asymptotically small error of complex models as a systematic "de-aliasing" that occurs in the over-parameterized regime. In the limit of large models, the contribution due to aliasing vanishes, leaving an expression for the asymptotic total error we call the invertibility failure of very large models on few training points. Because the generalized aliasing decomposition can be explicitly calculated from the relationship between model class and samples without seeing any data labels, it can answer questions related to experimental design and model selection before collecting data or performing experiments. We demonstrate this approach using several examples, including classical regression problems and a cluster expansion model used in materials science.

Tensor-reduced atomic density representations

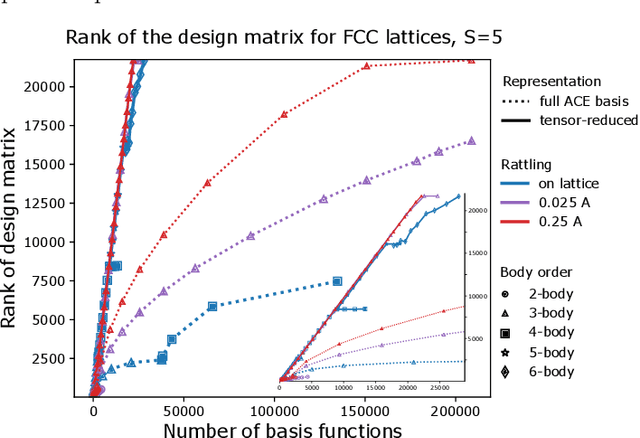
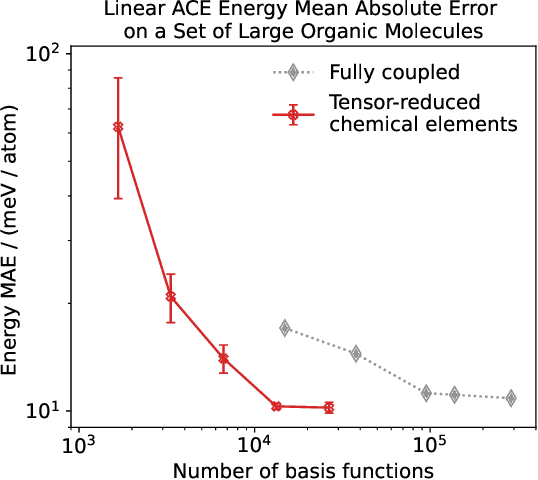
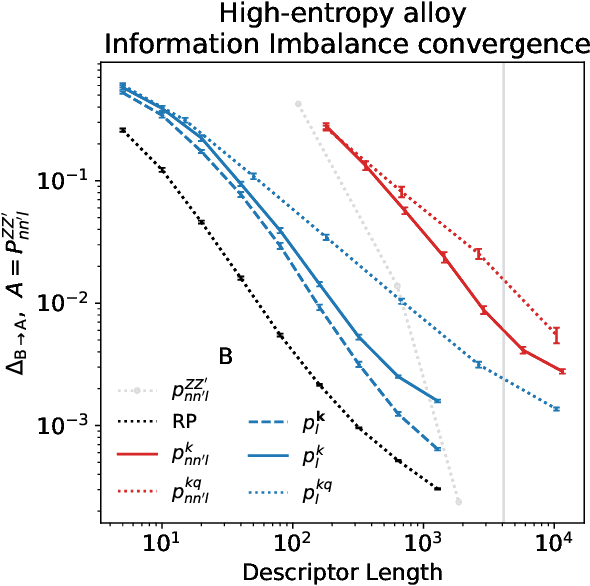
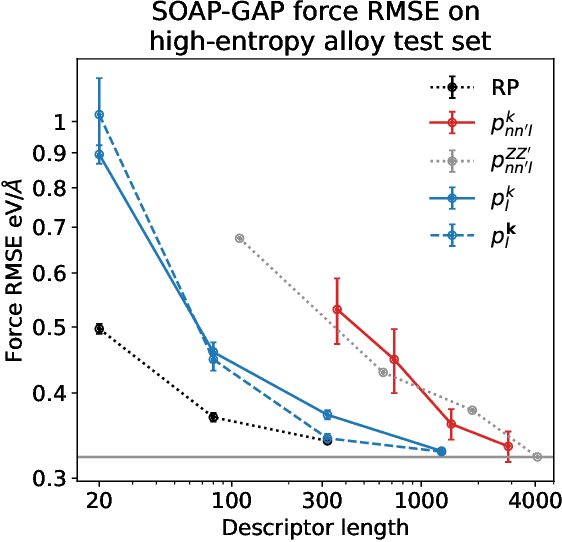
Density based representations of atomic environments that are invariant under Euclidean symmetries have become a widely used tool in the machine learning of interatomic potentials, broader data-driven atomistic modelling and the visualisation and analysis of materials datasets.The standard mechanism used to incorporate chemical element information is to create separate densities for each element and form tensor products between them. This leads to a steep scaling in the size of the representation as the number of elements increases. Graph neural networks, which do not explicitly use density representations, escape this scaling by mapping the chemical element information into a fixed dimensional space in a learnable way. We recast this approach as tensor factorisation by exploiting the tensor structure of standard neighbour density based descriptors. In doing so, we form compact tensor-reduced representations whose size does not depend on the number of chemical elements, but remain systematically convergeable and are therefore applicable to a wide range of data analysis and regression tasks.