Tensor-reduced atomic density representations

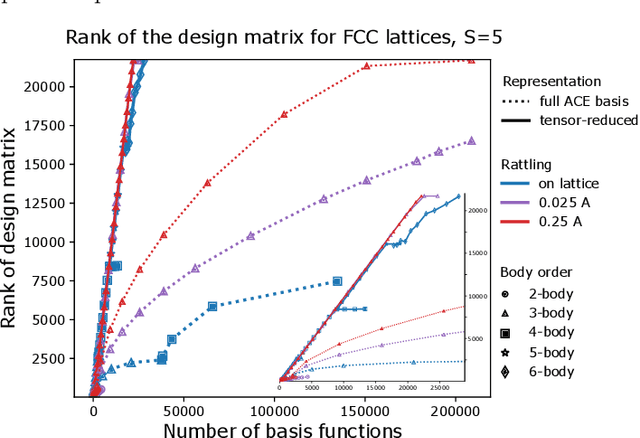
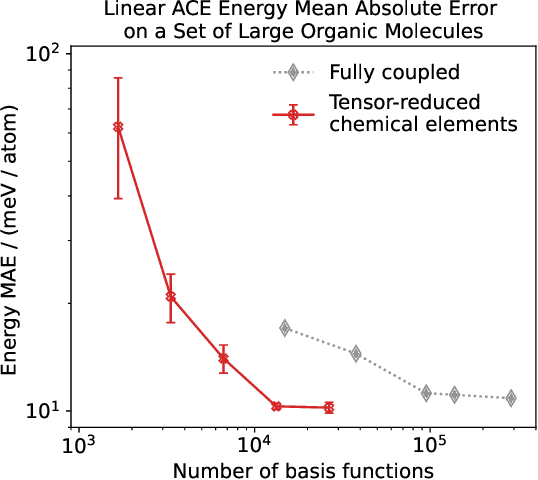
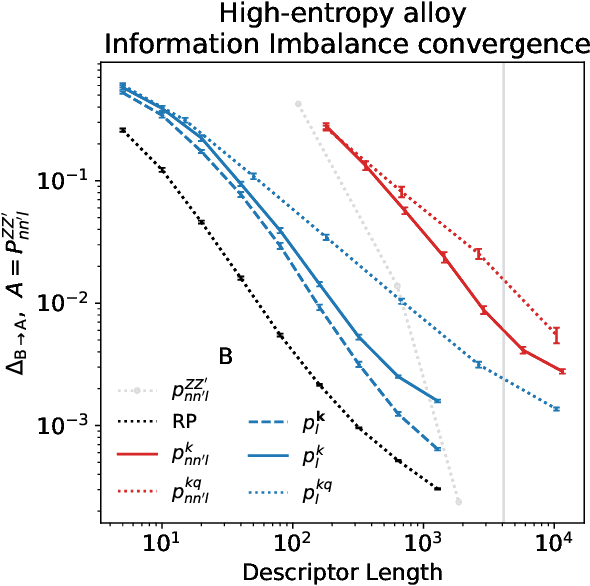
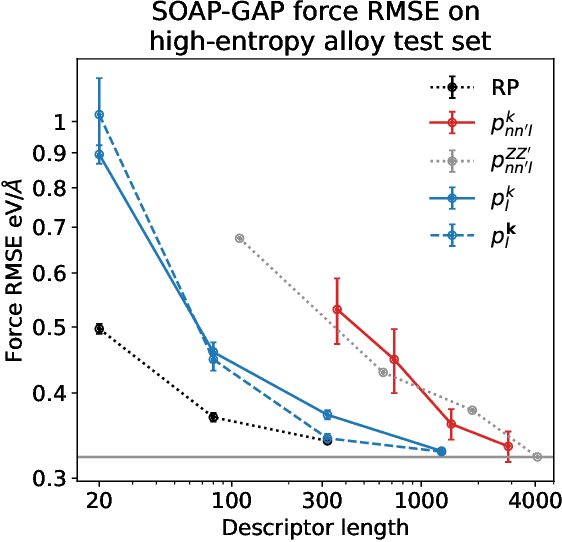
Density based representations of atomic environments that are invariant under Euclidean symmetries have become a widely used tool in the machine learning of interatomic potentials, broader data-driven atomistic modelling and the visualisation and analysis of materials datasets.The standard mechanism used to incorporate chemical element information is to create separate densities for each element and form tensor products between them. This leads to a steep scaling in the size of the representation as the number of elements increases. Graph neural networks, which do not explicitly use density representations, escape this scaling by mapping the chemical element information into a fixed dimensional space in a learnable way. We recast this approach as tensor factorisation by exploiting the tensor structure of standard neighbour density based descriptors. In doing so, we form compact tensor-reduced representations whose size does not depend on the number of chemical elements, but remain systematically convergeable and are therefore applicable to a wide range of data analysis and regression tasks.