Optimizing Data Distribution and Kernel Performance for Efficient Training of Chemistry Foundation Models: A Case Study with MACE

Chemistry Foundation Models (CFMs) that leverage Graph Neural Networks (GNNs) operating on 3D molecular graph structures are becoming indispensable tools for computational chemists and materials scientists. These models facilitate the understanding of matter and the discovery of new molecules and materials. In contrast to GNNs operating on a large homogeneous graphs, GNNs used by CFMs process a large number of geometric graphs of varying sizes, requiring different optimization strategies than those developed for large homogeneous GNNs. This paper presents optimizations for two critical phases of CFM training: data distribution and model training, targeting MACE - a state-of-the-art CFM. We address the challenge of load balancing in data distribution by formulating it as a multi-objective bin packing problem. We propose an iterative algorithm that provides a highly effective, fast, and practical solution, ensuring efficient data distribution. For the training phase, we identify symmetric tensor contraction as the key computational kernel in MACE and optimize this kernel to improve the overall performance. Our combined approach of balanced data distribution and kernel optimization significantly enhances the training process of MACE. Experimental results demonstrate a substantial speedup, reducing per-epoch execution time for training from 12 to 2 minutes on 740 GPUs with a 2.6M sample dataset.

BoostMD: Accelerating molecular sampling by leveraging ML force field features from previous time-steps

Simulating atomic-scale processes, such as protein dynamics and catalytic reactions, is crucial for advancements in biology, chemistry, and materials science. Machine learning force fields (MLFFs) have emerged as powerful tools that achieve near quantum mechanical accuracy, with promising generalization capabilities. However, their practical use is often limited by long inference times compared to classical force fields, especially when running extensive molecular dynamics (MD) simulations required for many biological applications. In this study, we introduce BoostMD, a surrogate model architecture designed to accelerate MD simulations. BoostMD leverages node features computed at previous time steps to predict energies and forces based on positional changes. This approach reduces the complexity of the learning task, allowing BoostMD to be both smaller and significantly faster than conventional MLFFs. During simulations, the computationally intensive reference MLFF is evaluated only every $N$ steps, while the lightweight BoostMD model handles the intermediate steps at a fraction of the computational cost. Our experiments demonstrate that BoostMD achieves an eight-fold speedup compared to the reference model and generalizes to unseen dipeptides. Furthermore, we find that BoostMD accurately samples the ground-truth Boltzmann distribution when running molecular dynamics. By combining efficient feature reuse with a streamlined architecture, BoostMD offers a robust solution for conducting large-scale, long-timescale molecular simulations, making high-accuracy ML-driven modeling more accessible and practical.

Zero Shot Molecular Generation via Similarity Kernels

Generative modelling aims to accelerate the discovery of novel chemicals by directly proposing structures with desirable properties. Recently, score-based, or diffusion, generative models have significantly outperformed previous approaches. Key to their success is the close relationship between the score and physical force, allowing the use of powerful equivariant neural networks. However, the behaviour of the learnt score is not yet well understood. Here, we analyse the score by training an energy-based diffusion model for molecular generation. We find that during the generation the score resembles a restorative potential initially and a quantum-mechanical force at the end. In between the two endpoints, it exhibits special properties that enable the building of large molecules. Using insights from the trained model, we present Similarity-based Molecular Generation (SiMGen), a new method for zero shot molecular generation. SiMGen combines a time-dependent similarity kernel with descriptors from a pretrained machine learning force field to generate molecules without any further training. Our approach allows full control over the molecular shape through point cloud priors and supports conditional generation. We also release an interactive web tool that allows users to generate structures with SiMGen online (https://zndraw.icp.uni-stuttgart.de).

Energy-conserving equivariant GNN for elasticity of lattice architected metamaterials

Lattices are architected metamaterials whose properties strongly depend on their geometrical design. The analogy between lattices and graphs enables the use of graph neural networks (GNNs) as a faster surrogate model compared to traditional methods such as finite element modelling. In this work we present a higher-order GNN model trained to predict the fourth-order stiffness tensor of periodic strut-based lattices. The key features of the model are (i) SE(3) equivariance, and (ii) consistency with the thermodynamic law of conservation of energy. We compare the model to non-equivariant models based on a number of error metrics and demonstrate the benefits of the encoded equivariance and energy conservation in terms of predictive performance and reduced training requirements.

A Geometric Insight into Equivariant Message Passing Neural Networks on Riemannian Manifolds

This work proposes a geometric insight into equivariant message passing on Riemannian manifolds. As previously proposed, numerical features on Riemannian manifolds are represented as coordinate-independent feature fields on the manifold. To any coordinate-independent feature field on a manifold comes attached an equivariant embedding of the principal bundle to the space of numerical features. We argue that the metric this embedding induces on the numerical feature space should optimally preserve the principal bundle's original metric. This optimality criterion leads to the minimization of a twisted form of the Polyakov action with respect to the graph of this embedding, yielding an equivariant diffusion process on the associated vector bundle. We obtain a message passing scheme on the manifold by discretizing the diffusion equation flow for a fixed time step. We propose a higher-order equivariant diffusion process equivalent to diffusion on the cartesian product of the base manifold. The discretization of the higher-order diffusion process on a graph yields a new general class of equivariant GNN, generalizing the ACE and MACE formalism to data on Riemannian manifolds.

Equivariant Matrix Function Neural Networks

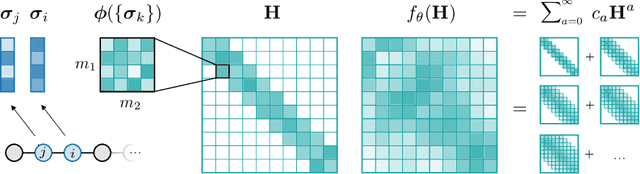
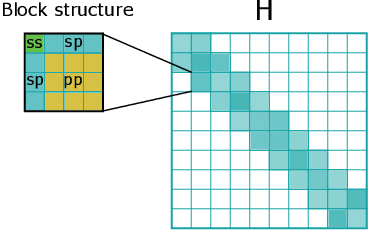
Graph Neural Networks (GNNs), especially message-passing neural networks (MPNNs), have emerged as powerful architectures for learning on graphs in diverse applications. However, MPNNs face challenges when modeling non-local interactions in systems such as large conjugated molecules, metals, or amorphous materials. Although Spectral GNNs and traditional neural networks such as recurrent neural networks and transformers mitigate these challenges, they often lack extensivity, adaptability, generalizability, computational efficiency, or fail to capture detailed structural relationships or symmetries in the data. To address these concerns, we introduce Matrix Function Neural Networks (MFNs), a novel architecture that parameterizes non-local interactions through analytic matrix equivariant functions. Employing resolvent expansions offers a straightforward implementation and the potential for linear scaling with system size. The MFN architecture achieves state-of-the-art performance in standard graph benchmarks, such as the ZINC and TU datasets, and is able to capture intricate non-local interactions in quantum systems, paving the way to new state-of-the-art force fields.

Retrieval of Boost Invariant Symbolic Observables via Feature Importance

Deep learning approaches for jet tagging in high-energy physics are characterized as black boxes that process a large amount of information from which it is difficult to extract key distinctive observables. In this proceeding, we present an alternative to deep learning approaches, Boost Invariant Polynomials, which enables direct analysis of simple analytic expressions representing the most important features in a given task. Further, we show how this approach provides an extremely low dimensional classifier with a minimum set of features representing %effective discriminating physically relevant observables and how it consequently speeds up the algorithm execution, with relatively close performance to the algorithm using the full information.

A General Framework for Equivariant Neural Networks on Reductive Lie Groups

Reductive Lie Groups, such as the orthogonal groups, the Lorentz group, or the unitary groups, play essential roles across scientific fields as diverse as high energy physics, quantum mechanics, quantum chromodynamics, molecular dynamics, computer vision, and imaging. In this paper, we present a general Equivariant Neural Network architecture capable of respecting the symmetries of the finite-dimensional representations of any reductive Lie Group G. Our approach generalizes the successful ACE and MACE architectures for atomistic point clouds to any data equivariant to a reductive Lie group action. We also introduce the lie-nn software library, which provides all the necessary tools to develop and implement such general G-equivariant neural networks. It implements routines for the reduction of generic tensor products of representations into irreducible representations, making it easy to apply our architecture to a wide range of problems and groups. The generality and performance of our approach are demonstrated by applying it to the tasks of top quark decay tagging (Lorentz group) and shape recognition (orthogonal group).

Evaluation of the MACE Force Field Architecture: from Medicinal Chemistry to Materials Science

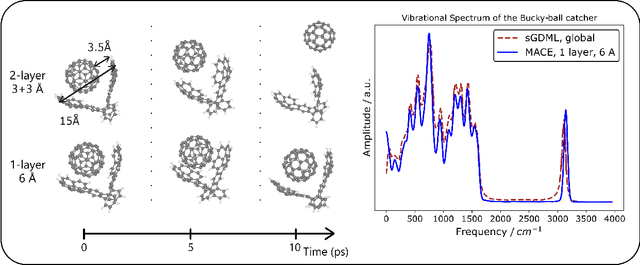
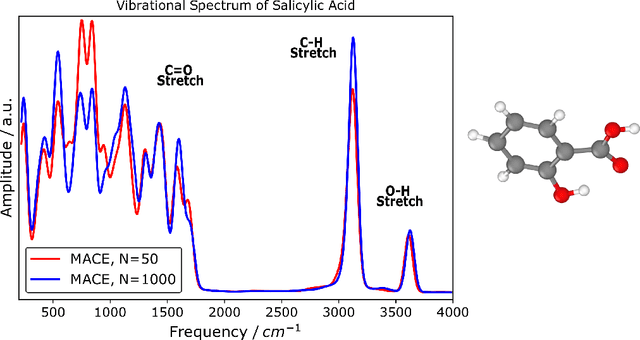
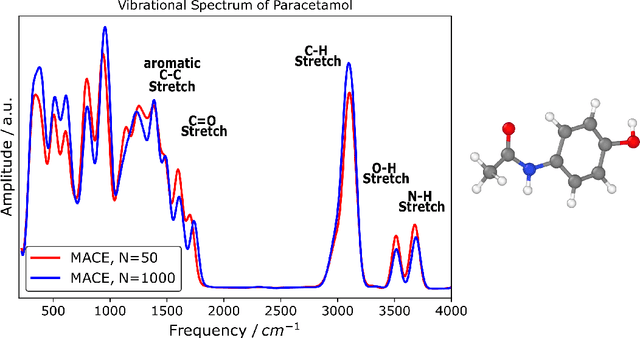
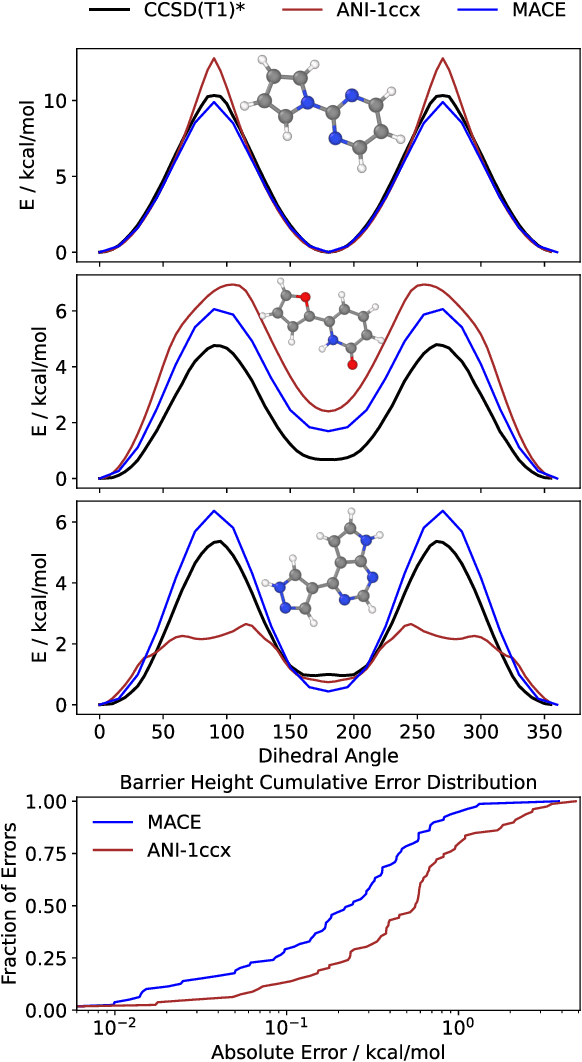
The MACE architecture represents the state of the art in the field of machine learning force fields for a variety of in-domain, extrapolation and low-data regime tasks. In this paper, we further evaluate MACE by fitting models for published benchmark datasets. We show that MACE generally outperforms alternatives for a wide range of systems from amorphous carbon and general small molecule organic chemistry to large molecules and liquid water. We demonstrate the capabilities of the model on tasks ranging from constrained geometry optimisation to molecular dynamics simulations and find excellent performance across all tested domains. We show that MACE is very data efficient, and can reproduce experimental molecular vibrational spectra when trained on as few as 50 randomly selected reference configurations. We further demonstrate that the strictly local atom-centered model is sufficient for such tasks even in the case of large molecules and weakly interacting molecular assemblies.

Tensor-reduced atomic density representations

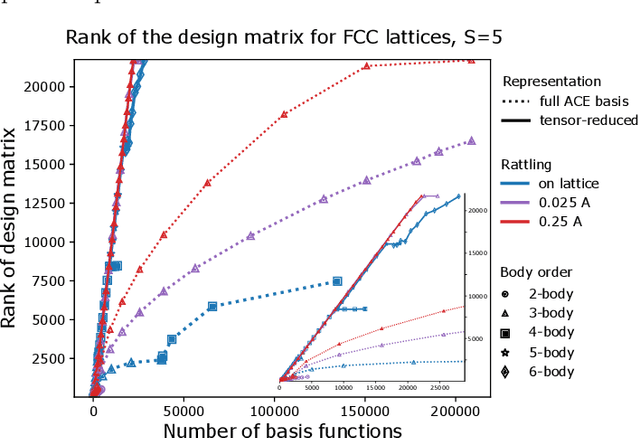
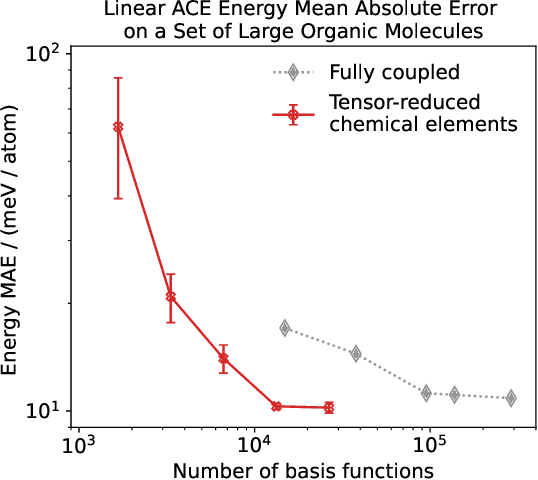
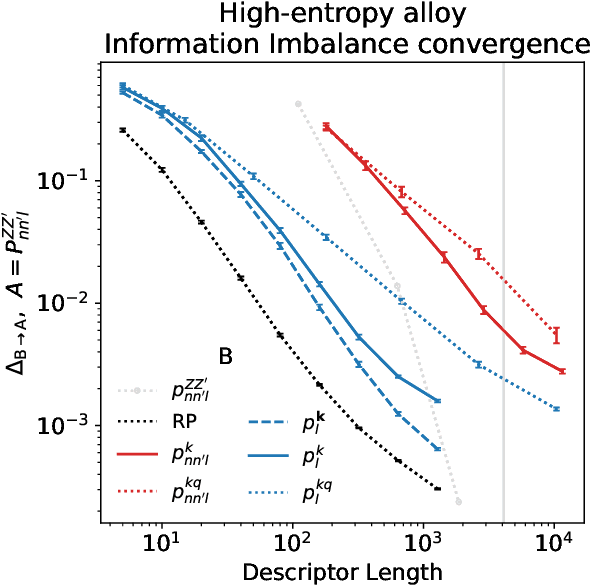
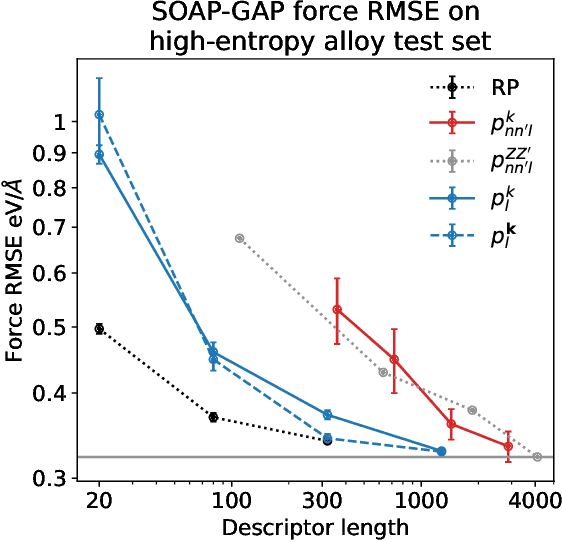
Density based representations of atomic environments that are invariant under Euclidean symmetries have become a widely used tool in the machine learning of interatomic potentials, broader data-driven atomistic modelling and the visualisation and analysis of materials datasets.The standard mechanism used to incorporate chemical element information is to create separate densities for each element and form tensor products between them. This leads to a steep scaling in the size of the representation as the number of elements increases. Graph neural networks, which do not explicitly use density representations, escape this scaling by mapping the chemical element information into a fixed dimensional space in a learnable way. We recast this approach as tensor factorisation by exploiting the tensor structure of standard neighbour density based descriptors. In doing so, we form compact tensor-reduced representations whose size does not depend on the number of chemical elements, but remain systematically convergeable and are therefore applicable to a wide range of data analysis and regression tasks.