Equivariant Matrix Function Neural Networks

Graph Neural Networks (GNNs), especially message-passing neural networks (MPNNs), have emerged as powerful architectures for learning on graphs in diverse applications. However, MPNNs face challenges when modeling non-local interactions in systems such as large conjugated molecules, metals, or amorphous materials. Although Spectral GNNs and traditional neural networks such as recurrent neural networks and transformers mitigate these challenges, they often lack extensivity, adaptability, generalizability, computational efficiency, or fail to capture detailed structural relationships or symmetries in the data. To address these concerns, we introduce Matrix Function Neural Networks (MFNs), a novel architecture that parameterizes non-local interactions through analytic matrix equivariant functions. Employing resolvent expansions offers a straightforward implementation and the potential for linear scaling with system size. The MFN architecture achieves state-of-the-art performance in standard graph benchmarks, such as the ZINC and TU datasets, and is able to capture intricate non-local interactions in quantum systems, paving the way to new state-of-the-art force fields.

Retrieval of Boost Invariant Symbolic Observables via Feature Importance

Deep learning approaches for jet tagging in high-energy physics are characterized as black boxes that process a large amount of information from which it is difficult to extract key distinctive observables. In this proceeding, we present an alternative to deep learning approaches, Boost Invariant Polynomials, which enables direct analysis of simple analytic expressions representing the most important features in a given task. Further, we show how this approach provides an extremely low dimensional classifier with a minimum set of features representing %effective discriminating physically relevant observables and how it consequently speeds up the algorithm execution, with relatively close performance to the algorithm using the full information.

A General Framework for Equivariant Neural Networks on Reductive Lie Groups

Reductive Lie Groups, such as the orthogonal groups, the Lorentz group, or the unitary groups, play essential roles across scientific fields as diverse as high energy physics, quantum mechanics, quantum chromodynamics, molecular dynamics, computer vision, and imaging. In this paper, we present a general Equivariant Neural Network architecture capable of respecting the symmetries of the finite-dimensional representations of any reductive Lie Group G. Our approach generalizes the successful ACE and MACE architectures for atomistic point clouds to any data equivariant to a reductive Lie group action. We also introduce the lie-nn software library, which provides all the necessary tools to develop and implement such general G-equivariant neural networks. It implements routines for the reduction of generic tensor products of representations into irreducible representations, making it easy to apply our architecture to a wide range of problems and groups. The generality and performance of our approach are demonstrated by applying it to the tasks of top quark decay tagging (Lorentz group) and shape recognition (orthogonal group).

Hyperactive Learning (HAL) for Data-Driven Interatomic Potentials

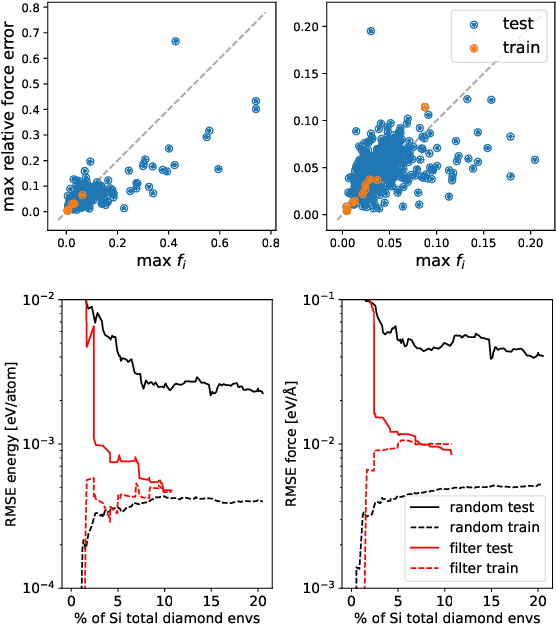
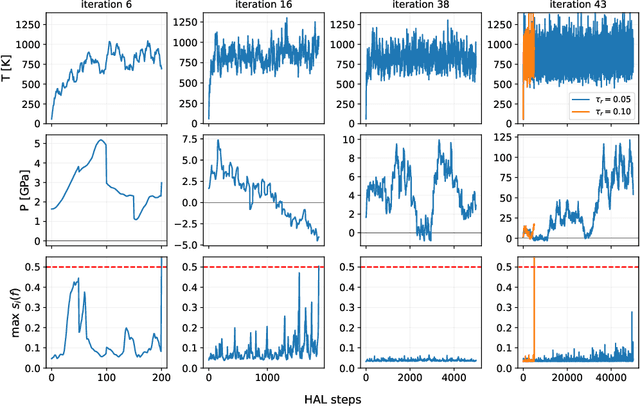
Data-driven interatomic potentials have emerged as a powerful class of surrogate models for ab initio potential energy surfaces that are able to reliably predict macroscopic properties with experimental accuracy. In generating accurate and transferable potentials the most time-consuming and arguably most important task is generating the training set, which still requires significant expert user input. To accelerate this process, this work presents hyperactive learning (HAL), a framework for formulating an accelerated sampling algorithm specifically for the task of training database generation. The overarching idea is to start from a physically motivated sampler (e.g., molecular dynamics) and a biasing term that drives the system towards high uncertainty and thus to unseen training configurations. Building on this framework, general protocols for building training databases for alloys and polymers leveraging the HAL framework will be presented. For alloys, fast (< 100 microsecond/atom/cpu-core) ACE potentials for AlSi10 are created that able to predict the melting temperature with good accuracy by fitting to a minimal HAL-generated database containing 88 configurations (32 atoms each) in 17 seconds using 8 cpu threads. For polymers, a HAL database is built using ACE able to determine the density of a long polyethylene glycol (PEG) polymer formed of 200 monomer units with experimental accuracy by only fitting to small isolated PEG polymers with sizes ranging from 2 to 32.

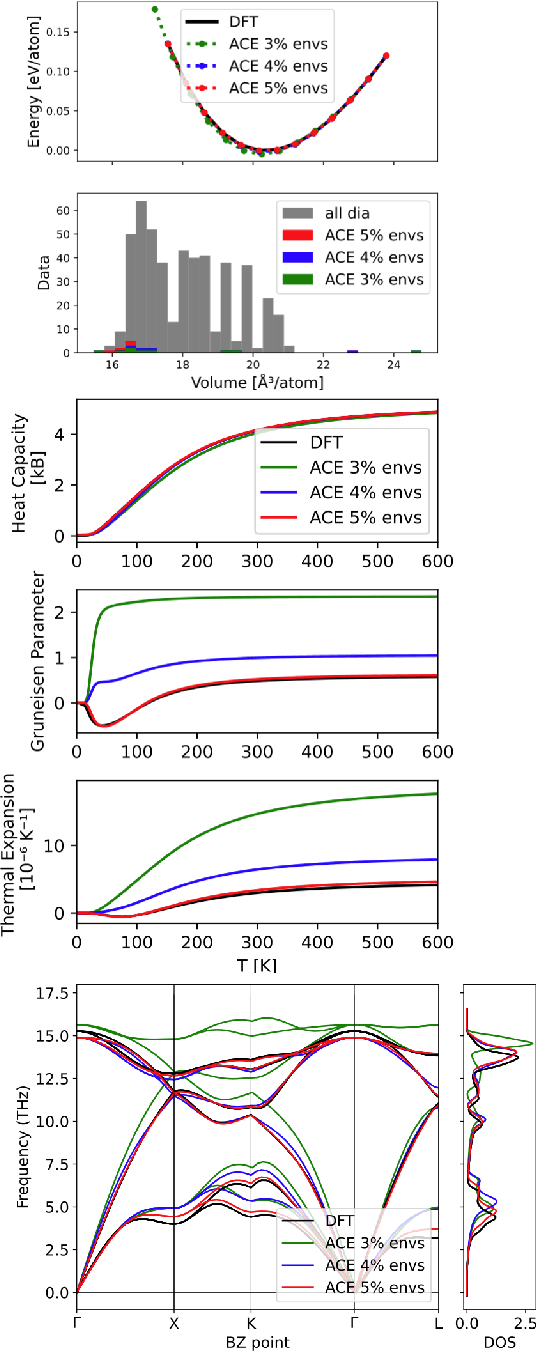
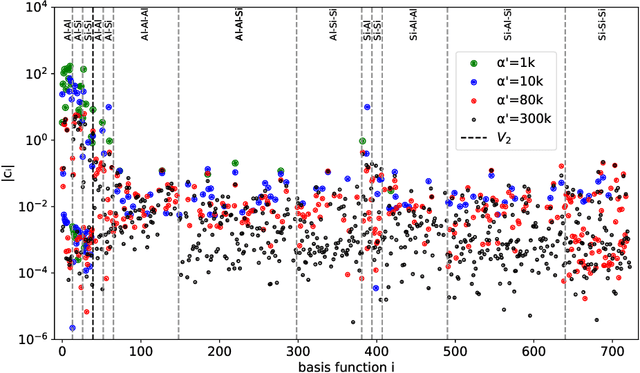
Tensor-reduced atomic density representations

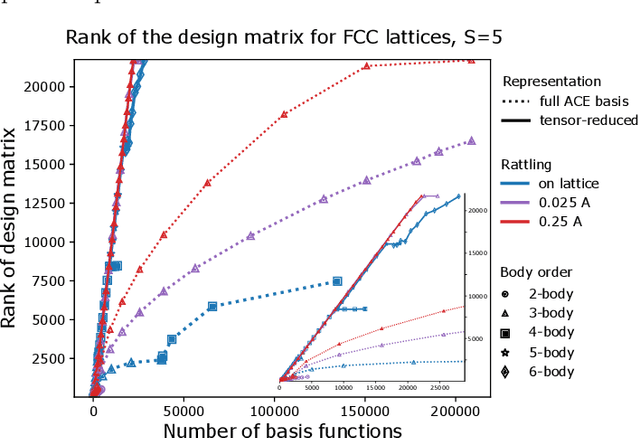
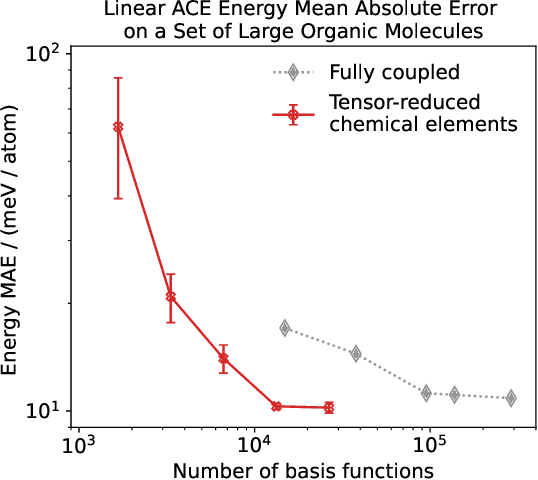
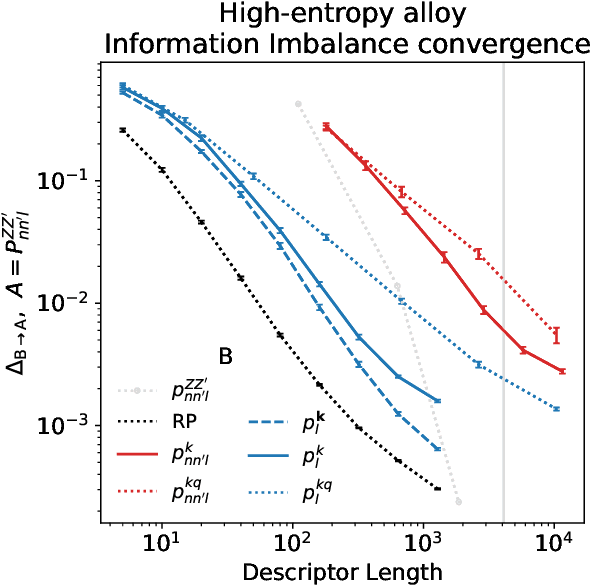
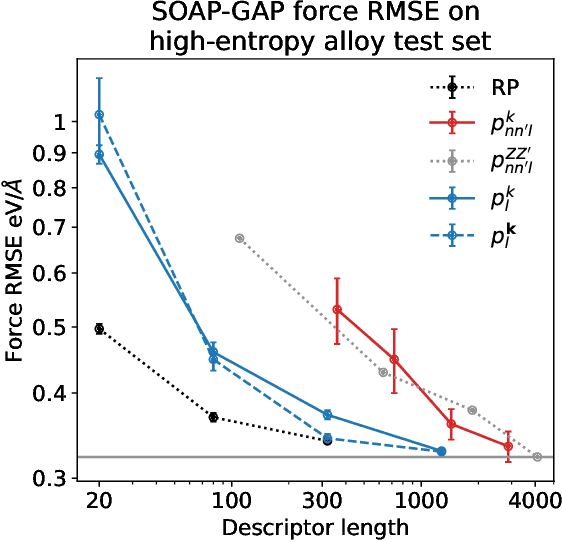
Density based representations of atomic environments that are invariant under Euclidean symmetries have become a widely used tool in the machine learning of interatomic potentials, broader data-driven atomistic modelling and the visualisation and analysis of materials datasets.The standard mechanism used to incorporate chemical element information is to create separate densities for each element and form tensor products between them. This leads to a steep scaling in the size of the representation as the number of elements increases. Graph neural networks, which do not explicitly use density representations, escape this scaling by mapping the chemical element information into a fixed dimensional space in a learnable way. We recast this approach as tensor factorisation by exploiting the tensor structure of standard neighbour density based descriptors. In doing so, we form compact tensor-reduced representations whose size does not depend on the number of chemical elements, but remain systematically convergeable and are therefore applicable to a wide range of data analysis and regression tasks.

BIP: Boost Invariant Polynomials for Efficient Jet Tagging

Deep Learning approaches are becoming the go-to methods for data analysis in High Energy Physics (HEP). Nonetheless, most physics-inspired modern architectures are computationally inefficient and lack interpretability. This is especially the case with jet tagging algorithms, where computational efficiency is crucial considering the large amounts of data produced by modern particle detectors. In this work, we present a novel, versatile and transparent framework for jet representation; invariant to Lorentz group boosts, which achieves high accuracy on jet tagging benchmarks while being orders of magnitudes faster to train and evaluate than other modern approaches for both supervised and unsupervised schemes.

MACE: Higher Order Equivariant Message Passing Neural Networks for Fast and Accurate Force Fields

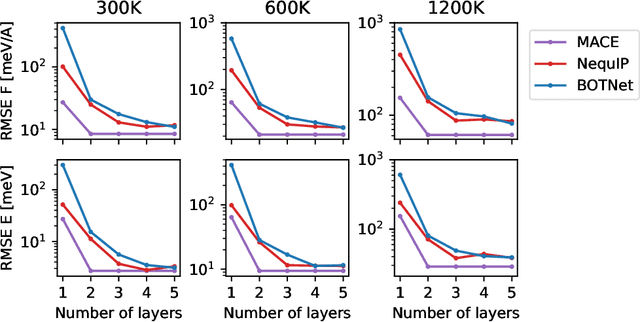
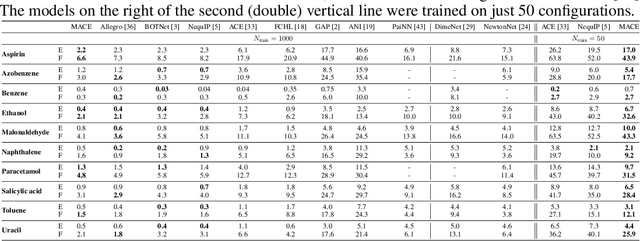
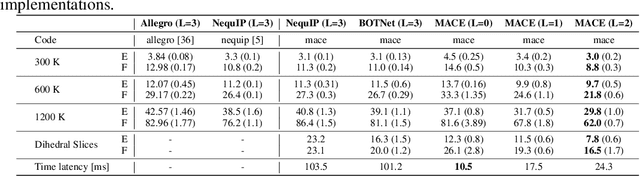
Creating fast and accurate force fields is a long-standing challenge in computational chemistry and materials science. Recently, several equivariant message passing neural networks (MPNNs) have been shown to outperform models built using other approaches in terms of accuracy. However, most MPNNs suffer from high computational cost and poor scalability. We propose that these limitations arise because MPNNs only pass two-body messages leading to a direct relationship between the number of layers and the expressivity of the network. In this work, we introduce MACE, a new equivariant MPNN model that uses higher body order messages. In particular, we show that using four-body messages reduces the required number of message passing iterations to just \emph{two}, resulting in a fast and highly parallelizable model, reaching or exceeding state-of-the-art accuracy on the rMD17, 3BPA, and AcAc benchmark tasks. We also demonstrate that using higher order messages leads to an improved steepness of the learning curves.

The Design Space of E-Equivariant Atom-Centered Interatomic Potentials

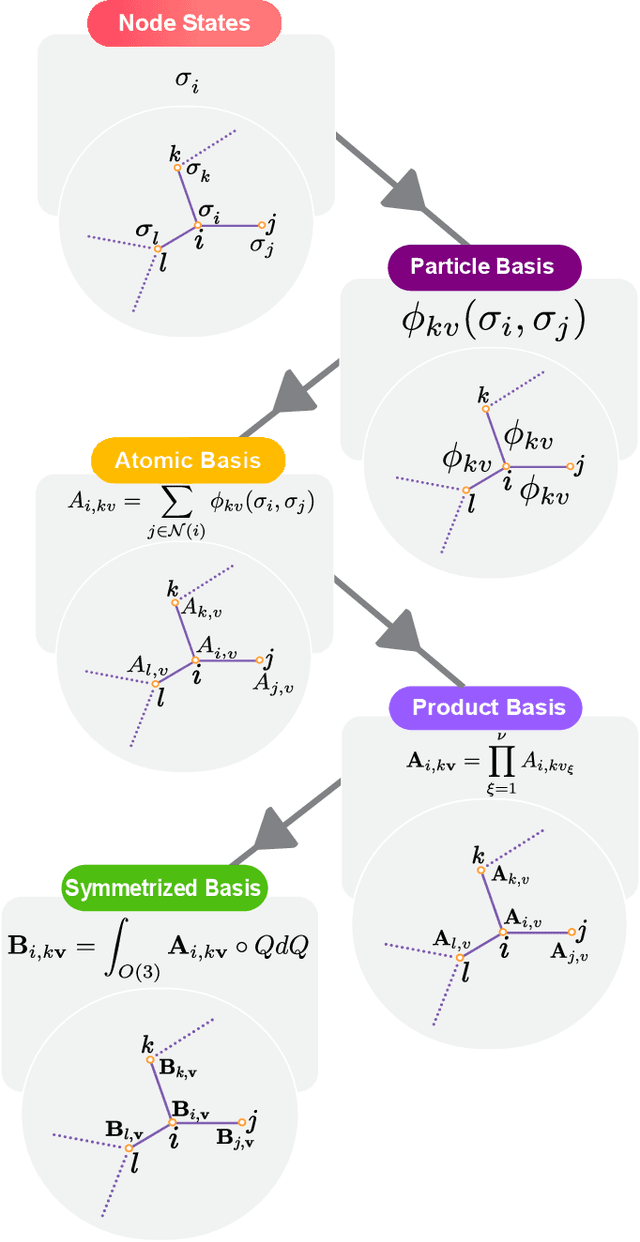
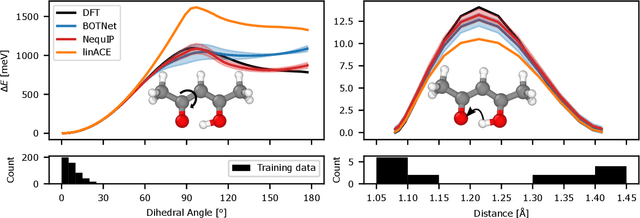
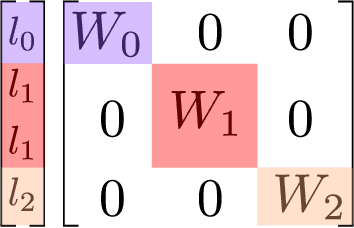
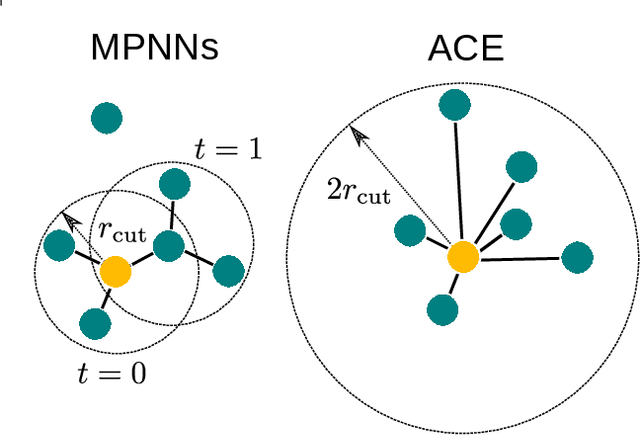
The rapid progress of machine learning interatomic potentials over the past couple of years produced a number of new architectures. Particularly notable among these are the Atomic Cluster Expansion (ACE), which unified many of the earlier ideas around atom density-based descriptors, and Neural Equivariant Interatomic Potentials (NequIP), a message passing neural network with equivariant features that showed state of the art accuracy. In this work, we construct a mathematical framework that unifies these models: ACE is generalised so that it can be recast as one layer of a multi-layer architecture. From another point of view, the linearised version of NequIP is understood as a particular sparsification of a much larger polynomial model. Our framework also provides a practical tool for systematically probing different choices in the unified design space. We demonstrate this by an ablation study of NequIP via a set of experiments looking at in- and out-of-domain accuracy and smooth extrapolation very far from the training data, and shed some light on which design choices are critical for achieving high accuracy. Finally, we present BOTNet (Body-Ordered-Tensor-Network), a much-simplified version of NequIP, which has an interpretable architecture and maintains accuracy on benchmark datasets.