Far from Asymptopia

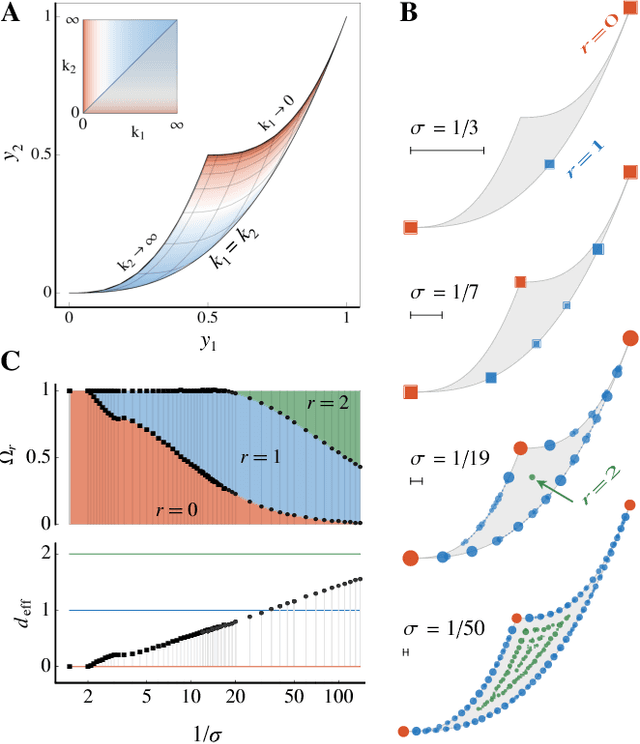
Inference from limited data requires a notion of measure on parameter space, which is most explicit in the Bayesian framework as a prior distribution. Jeffreys prior is the best-known uninformative choice, the invariant volume element from information geometry, but we demonstrate here that this leads to enormous bias in typical high-dimensional models. This is because models found in science typically have an effective dimensionality of accessible behaviours much smaller than the number of microscopic parameters. Any measure which treats all of these parameters equally is far from uniform when projected onto the sub-space of relevant parameters, due to variations in the local co-volume of irrelevant directions. We present results on a principled choice of measure which avoids this issue, and leads to unbiased posteriors, by focusing on relevant parameters. This optimal prior depends on the quantity of data to be gathered, and approaches Jeffreys prior in the asymptotic limit. But for typical models this limit cannot be justified without an impossibly large increase in the quantity of data, exponential in the number of microscopic parameters.

Maximizing the information learned from finite data selects a simple model

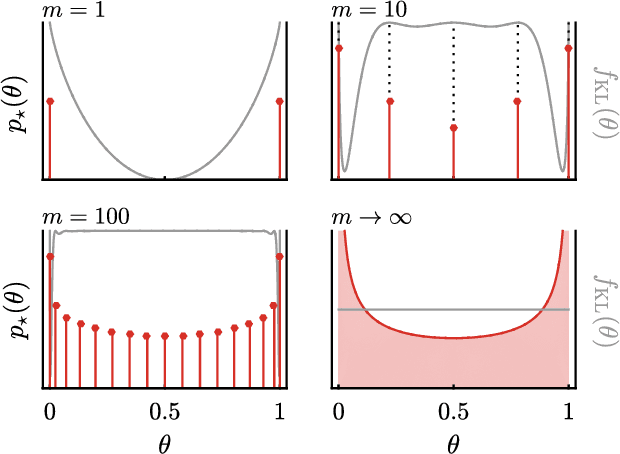
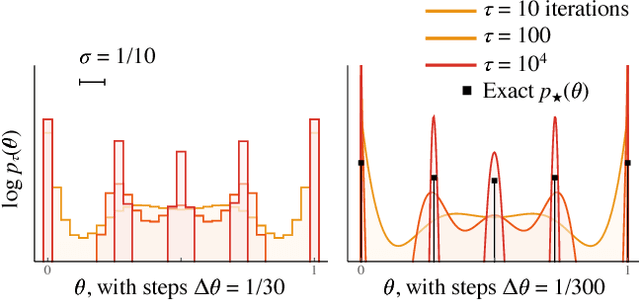
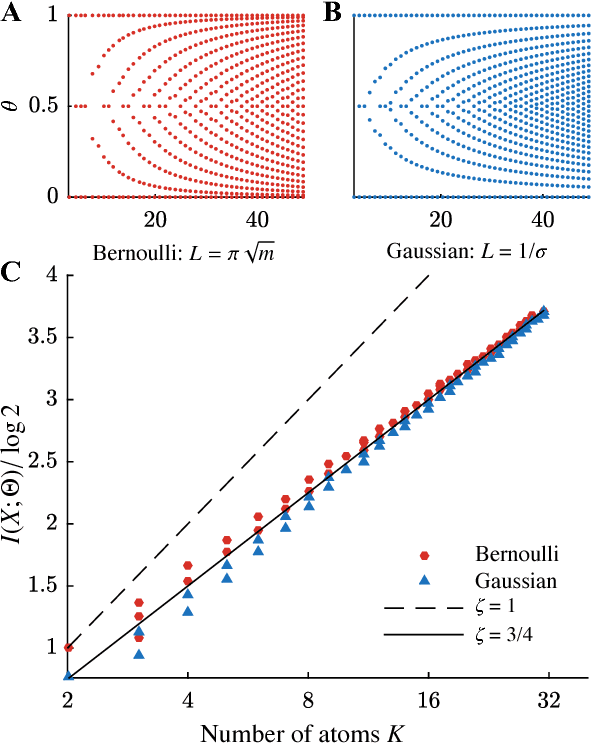
We use the language of uninformative Bayesian prior choice to study the selection of appropriately simple effective models. We advocate for the prior which maximizes the mutual information between parameters and predictions, learning as much as possible from limited data. When many parameters are poorly constrained by the available data, we find that this prior puts weight only on boundaries of the parameter manifold. Thus it selects a lower-dimensional effective theory in a principled way, ignoring irrelevant parameter directions. In the limit where there is sufficient data to tightly constrain any number of parameters, this reduces to Jeffreys prior. But we argue that this limit is pathological when applied to the hyper-ribbon parameter manifolds generic in science, because it leads to dramatic dependence on effects invisible to experiment.