Maximizing the information learned from finite data selects a simple model
Paper and Code
Feb 14, 2018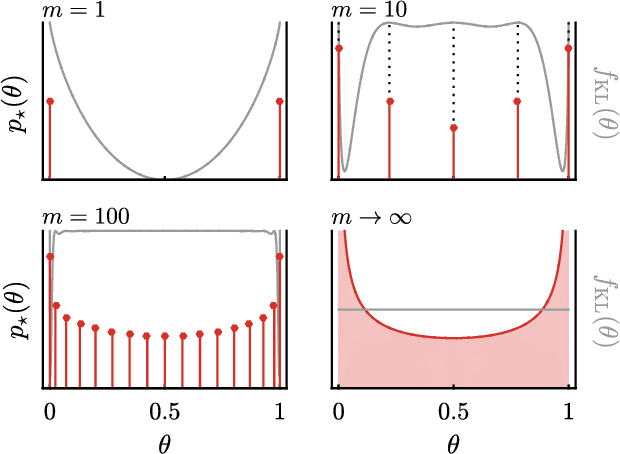
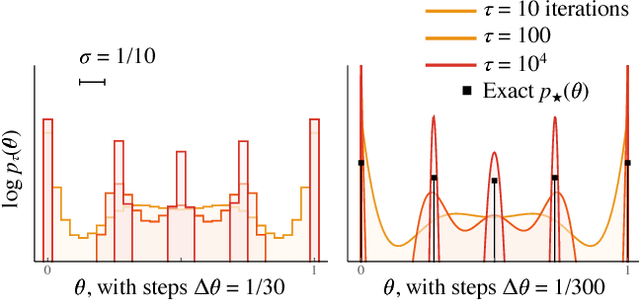
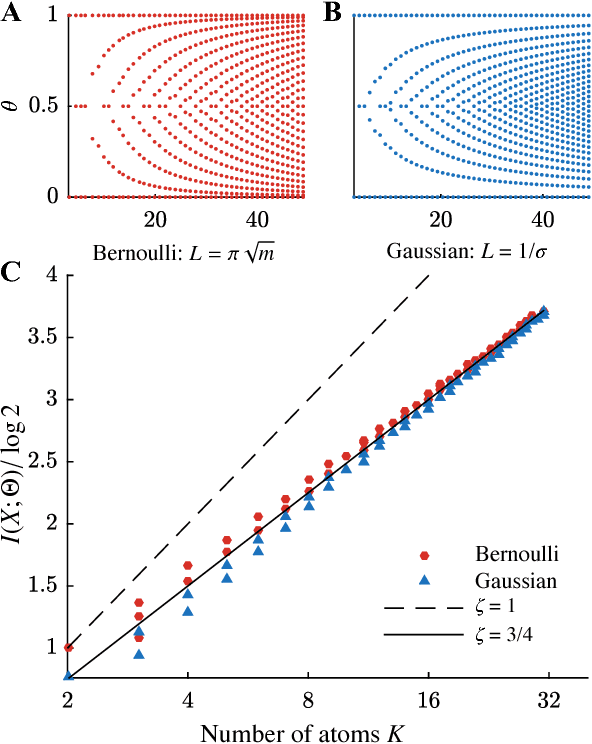
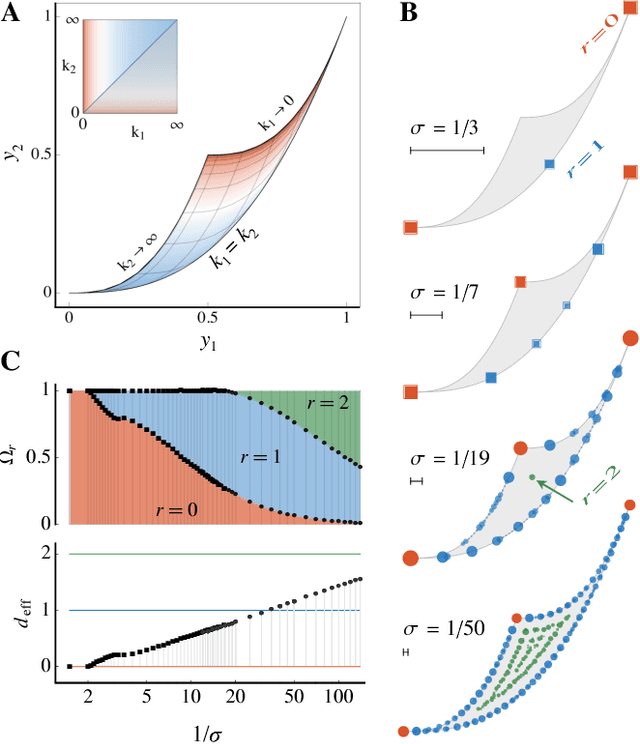
We use the language of uninformative Bayesian prior choice to study the selection of appropriately simple effective models. We advocate for the prior which maximizes the mutual information between parameters and predictions, learning as much as possible from limited data. When many parameters are poorly constrained by the available data, we find that this prior puts weight only on boundaries of the parameter manifold. Thus it selects a lower-dimensional effective theory in a principled way, ignoring irrelevant parameter directions. In the limit where there is sufficient data to tightly constrain any number of parameters, this reduces to Jeffreys prior. But we argue that this limit is pathological when applied to the hyper-ribbon parameter manifolds generic in science, because it leads to dramatic dependence on effects invisible to experiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge