$Γ$-VAE: Curvature regularized variational autoencoders for uncovering emergent low dimensional geometric structure in high dimensional data

Natural systems with emergent behaviors often organize along low-dimensional subsets of high-dimensional spaces. For example, despite the tens of thousands of genes in the human genome, the principled study of genomics is fruitful because biological processes rely on coordinated organization that results in lower dimensional phenotypes. To uncover this organization, many nonlinear dimensionality reduction techniques have successfully embedded high-dimensional data into low-dimensional spaces by preserving local similarities between data points. However, the nonlinearities in these methods allow for too much curvature to preserve general trends across multiple non-neighboring data clusters, thereby limiting their interpretability and generalizability to out-of-distribution data. Here, we address both of these limitations by regularizing the curvature of manifolds generated by variational autoencoders, a process we coin ``$\Gamma$-VAE''. We demonstrate its utility using two example data sets: bulk RNA-seq from the The Cancer Genome Atlas (TCGA) and the Genotype Tissue Expression (GTEx); and single cell RNA-seq from a lineage tracing experiment in hematopoietic stem cell differentiation. We find that the resulting regularized manifolds identify mesoscale structure associated with different cancer cell types, and accurately re-embed tissues from completely unseen, out-of distribution cancers as if they were originally trained on them. Finally, we show that preserving long-range relationships to differentiated cells separates undifferentiated cells -- which have not yet specialized -- according to their eventual fate. Broadly, we anticipate that regularizing the curvature of generative models will enable more consistent, predictive, and generalizable models in any high-dimensional system with emergent low-dimensional behavior.

The Training Process of Many Deep Networks Explores the Same Low-Dimensional Manifold

We develop information-geometric techniques to analyze the trajectories of the predictions of deep networks during training. By examining the underlying high-dimensional probabilistic models, we reveal that the training process explores an effectively low-dimensional manifold. Networks with a wide range of architectures, sizes, trained using different optimization methods, regularization techniques, data augmentation techniques, and weight initializations lie on the same manifold in the prediction space. We study the details of this manifold to find that networks with different architectures follow distinguishable trajectories but other factors have a minimal influence; larger networks train along a similar manifold as that of smaller networks, just faster; and networks initialized at very different parts of the prediction space converge to the solution along a similar manifold.

A picture of the space of typical learnable tasks

We develop a technique to analyze representations learned by deep networks when they are trained on different tasks using supervised, meta- and contrastive learning. We develop a technique to visualize such representations using an isometric embedding of the space of probabilistic models into a lower-dimensional space, i.e., one that preserves pairwise distances. We discover the following surprising phenomena that shed light upon the structure in the space of learnable tasks: (1) the manifold of probabilistic models trained on different tasks using different representation learning methods is effectively low-dimensional; (2) supervised learning on one task results in a surprising amount of progress on seemingly dissimilar tasks; progress on other tasks is larger if the training task has diverse classes; (3) the structure of the space of tasks indicated by our analysis is consistent with parts of the Wordnet phylogenetic tree; (4) fine-tuning a model upon a sub-task does not change the representation much if the model was trained for a large number of epochs; (5) episodic meta-learning algorithms fit similar models eventually as that of supervised learning, even if the two traverse different trajectories during training; (6) contrastive learning methods trained on different datasets learn similar representations. We use classification tasks constructed from the CIFAR-10 and Imagenet datasets to study these phenomena.

Jeffrey's prior sampling of deep sigmoidal networks

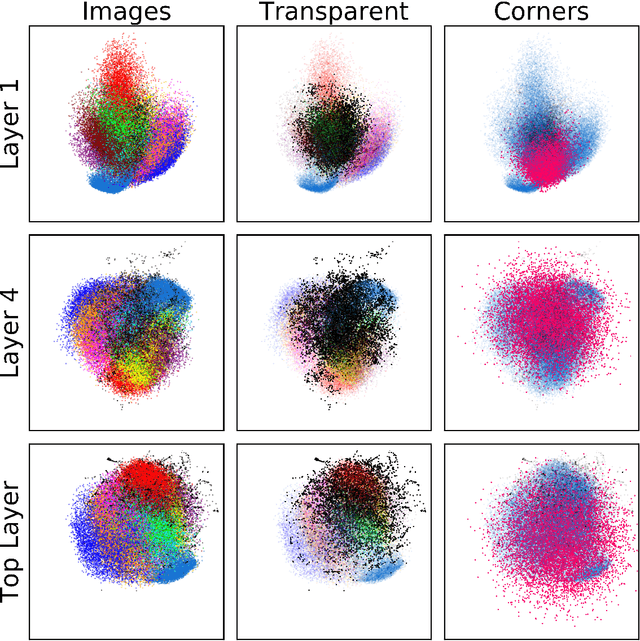
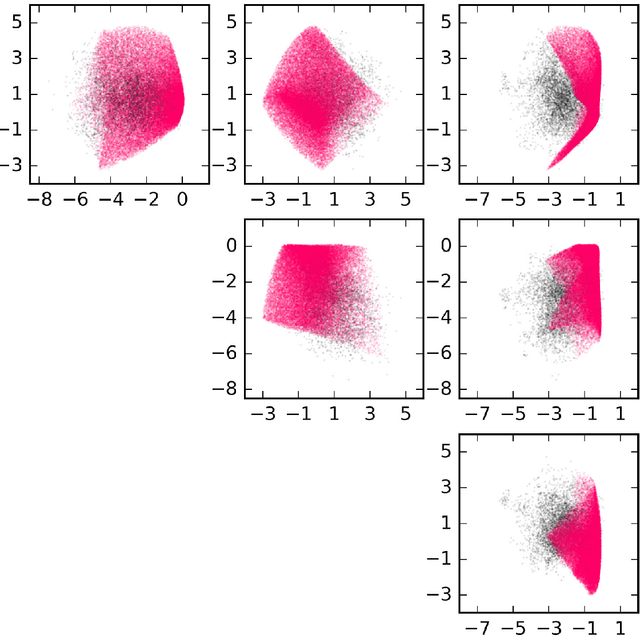
Neural networks have been shown to have a remarkable ability to uncover low dimensional structure in data: the space of possible reconstructed images form a reduced model manifold in image space. We explore this idea directly by analyzing the manifold learned by Deep Belief Networks and Stacked Denoising Autoencoders using Monte Carlo sampling. The model manifold forms an only slightly elongated hyperball with actual reconstructed data appearing predominantly on the boundaries of the manifold. In connection with the results we present, we discuss problems of sampling high-dimensional manifolds as well as recent work [M. Transtrum, G. Hart, and P. Qiu, Submitted (2014)] discussing the relation between high dimensional geometry and model reduction.