Jeffrey's prior sampling of deep sigmoidal networks
Paper and Code
May 25, 2017
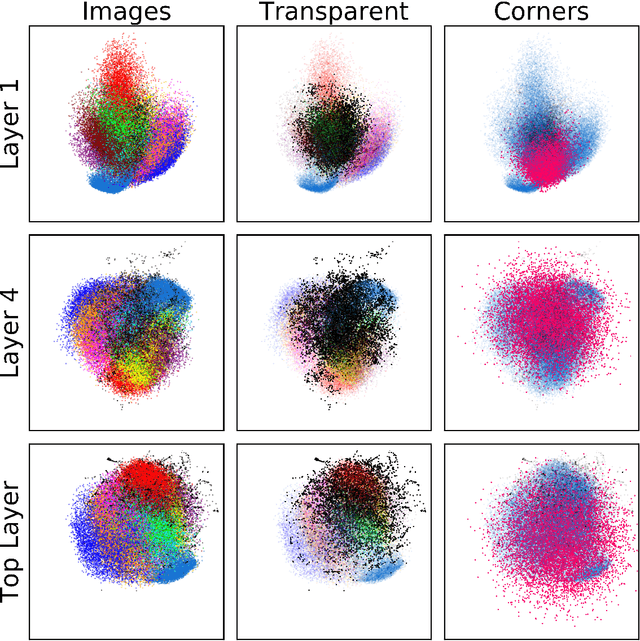

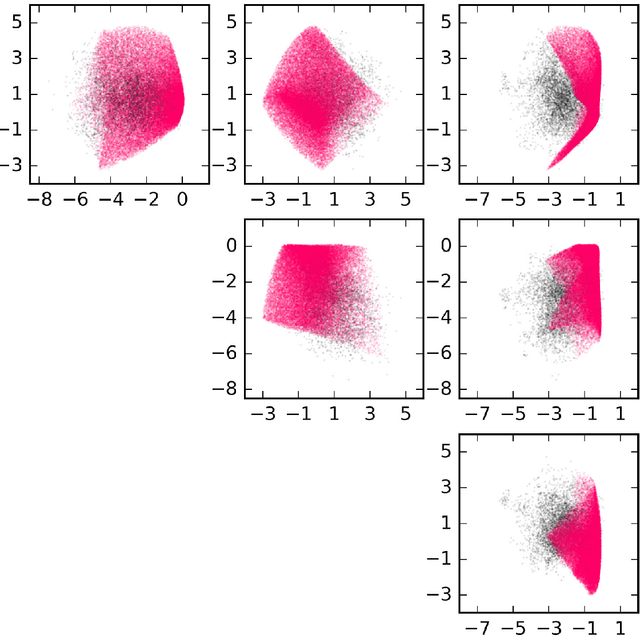
Neural networks have been shown to have a remarkable ability to uncover low dimensional structure in data: the space of possible reconstructed images form a reduced model manifold in image space. We explore this idea directly by analyzing the manifold learned by Deep Belief Networks and Stacked Denoising Autoencoders using Monte Carlo sampling. The model manifold forms an only slightly elongated hyperball with actual reconstructed data appearing predominantly on the boundaries of the manifold. In connection with the results we present, we discuss problems of sampling high-dimensional manifolds as well as recent work [M. Transtrum, G. Hart, and P. Qiu, Submitted (2014)] discussing the relation between high dimensional geometry and model reduction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge