Optimal control of the future via prospective learning with control

Optimal control of the future is the next frontier for AI. Current approaches to this problem are typically rooted in either reinforcement learning (RL). While powerful, this learning framework is mathematically distinct from supervised learning, which has been the main workhorse for the recent achievements in AI. Moreover, RL typically operates in a stationary environment with episodic resets, limiting its utility to more realistic settings. Here, we extend supervised learning to address learning to control in non-stationary, reset-free environments. Using this framework, called ''Prospective Learning with Control (PL+C)'', we prove that under certain fairly general assumptions, empirical risk minimization (ERM) asymptotically achieves the Bayes optimal policy. We then consider a specific instance of prospective learning with control, foraging -- which is a canonical task for any mobile agent -- be it natural or artificial. We illustrate that modern RL algorithms fail to learn in these non-stationary reset-free environments, and even with modifications, they are orders of magnitude less efficient than our prospective foraging agents.

Prospective Learning in Retrospect

In most real-world applications of artificial intelligence, the distributions of the data and the goals of the learners tend to change over time. The Probably Approximately Correct (PAC) learning framework, which underpins most machine learning algorithms, fails to account for dynamic data distributions and evolving objectives, often resulting in suboptimal performance. Prospective learning is a recently introduced mathematical framework that overcomes some of these limitations. We build on this framework to present preliminary results that improve the algorithm and numerical results, and extend prospective learning to sequential decision-making scenarios, specifically foraging. Code is available at: https://github.com/neurodata/prolearn2.

Prospective Learning: Learning for a Dynamic Future

In real-world applications, the distribution of the data, and our goals, evolve over time. The prevailing theoretical framework for studying machine learning, namely probably approximately correct (PAC) learning, largely ignores time. As a consequence, existing strategies to address the dynamic nature of data and goals exhibit poor real-world performance. This paper develops a theoretical framework called "Prospective Learning" that is tailored for situations when the optimal hypothesis changes over time. In PAC learning, empirical risk minimization (ERM) is known to be consistent. We develop a learner called Prospective ERM, which returns a sequence of predictors that make predictions on future data. We prove that the risk of prospective ERM converges to the Bayes risk under certain assumptions on the stochastic process generating the data. Prospective ERM, roughly speaking, incorporates time as an input in addition to the data. We show that standard ERM as done in PAC learning, without incorporating time, can result in failure to learn when distributions are dynamic. Numerical experiments illustrate that prospective ERM can learn synthetic and visual recognition problems constructed from MNIST and CIFAR-10.

Approximately optimal domain adaptation with Fisher's Linear Discriminant Analysis

We propose a class of models based on Fisher's Linear Discriminant (FLD) in the context of domain adaptation. The class is the convex combination of two hypotheses: i) an average hypothesis representing previously seen source tasks and ii) a hypothesis trained on a new target task. For a particular generative setting we derive the optimal convex combination of the two models under 0-1 loss, propose a computable approximation, and study the effect of various parameter settings on the relative risks between the optimal hypothesis, hypothesis i), and hypothesis ii). We demonstrate the effectiveness of the proposed optimal classifier in the context of EEG- and ECG-based classification settings and argue that the optimal classifier can be computed without access to direct information from any of the individual source tasks. We conclude by discussing further applications, limitations, and possible future directions.

The Value of Out-of-Distribution Data

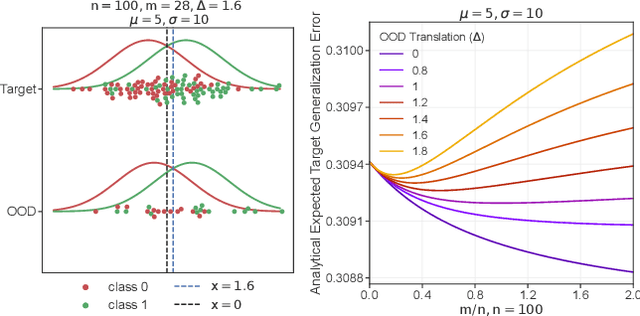
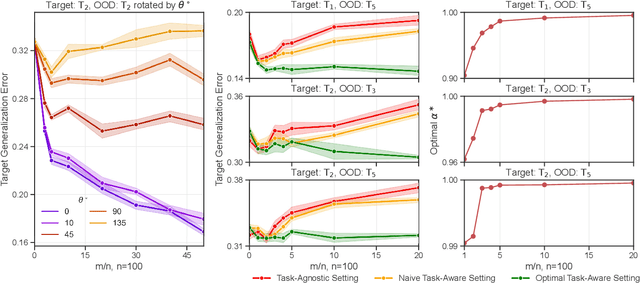
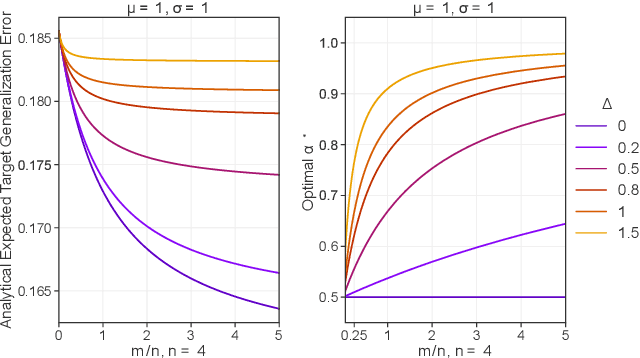
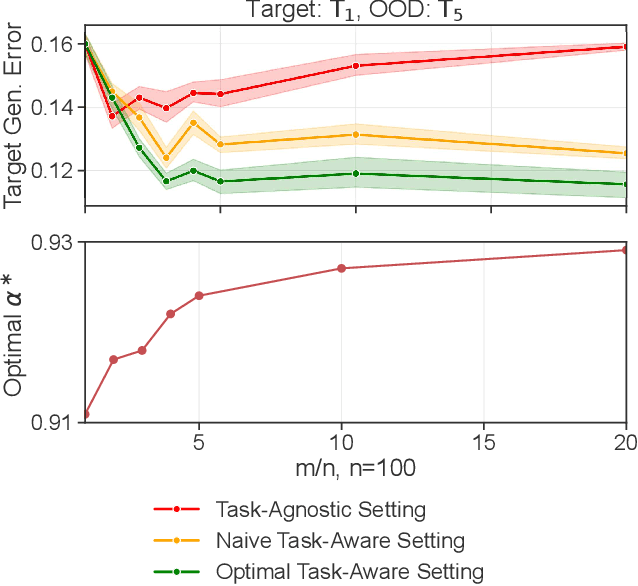
More data helps us generalize to a task. But real datasets can contain out-of-distribution (OOD) data; this can come in the form of heterogeneity such as intra-class variability but also in the form of temporal shifts or concept drifts. We demonstrate a counter-intuitive phenomenon for such problems: generalization error of the task can be a non-monotonic function of the number of OOD samples; a small number of OOD samples can improve generalization but if the number of OOD samples is beyond a threshold, then the generalization error can deteriorate. We also show that if we know which samples are OOD, then using a weighted objective between the target and OOD samples ensures that the generalization error decreases monotonically. We demonstrate and analyze this issue using linear classifiers on synthetic datasets and medium-sized neural networks on CIFAR-10.

Out-of-distribution and in-distribution posterior calibration using Kernel Density Polytopes

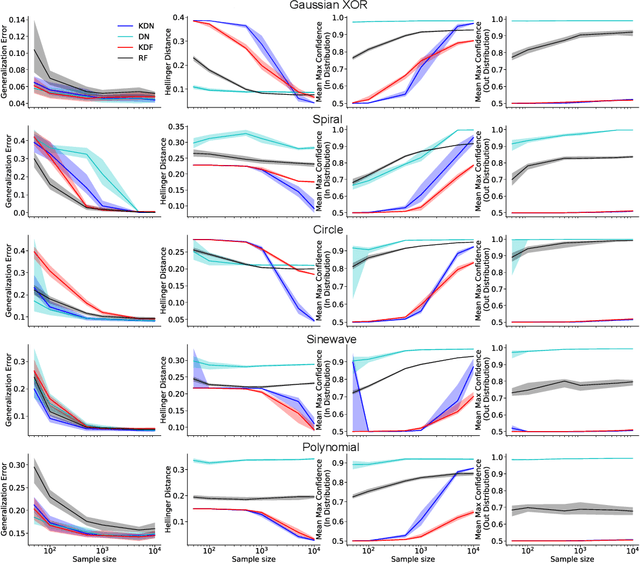
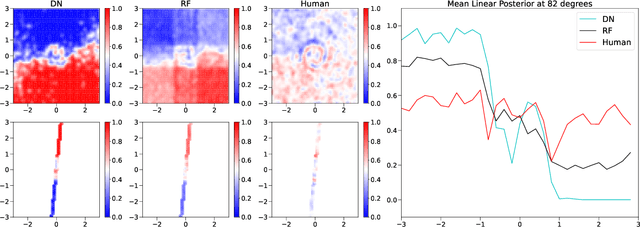
Any reasonable machine learning (ML) model should not only interpolate efficiently in between the training samples provided (in-distribution region), but also approach the extrapolative or out-of-distribution (OOD) region without being overconfident. Our experiment on human subjects justifies the aforementioned properties for human intelligence as well. Many state-of-the-art algorithms have tried to fix the overconfidence problem of ML models in the OOD region. However, in doing so, they have often impaired the in-distribution performance of the model. Our key insight is that ML models partition the feature space into polytopes and learn constant (random forests) or affine (ReLU networks) functions over those polytopes. This leads to the OOD overconfidence problem for the polytopes which lie in the training data boundary and extend to infinity. To resolve this issue, we propose kernel density methods that fit Gaussian kernel over the polytopes, which are learned using ML models. Specifically, we introduce two variants of kernel density polytopes: Kernel Density Forest (KDF) and Kernel Density Network (KDN) based on random forests and deep networks, respectively. Studies on various simulation settings show that both KDF and KDN achieve uniform confidence over the classes in the OOD region while maintaining good in-distribution accuracy compared to that of their respective parent models.

Towards Accurate Cross-Domain In-Bed Human Pose Estimation

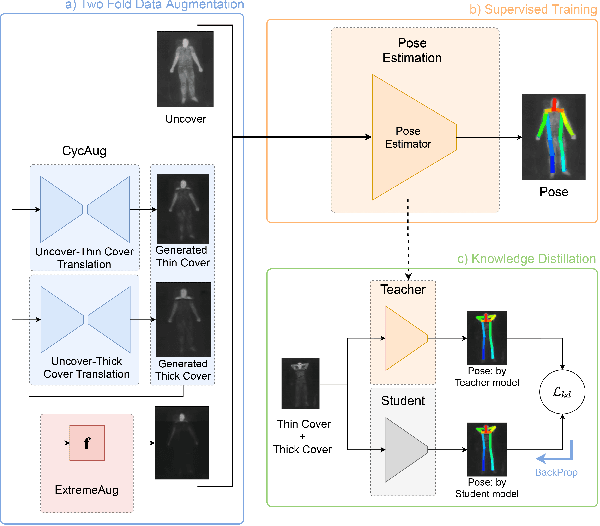
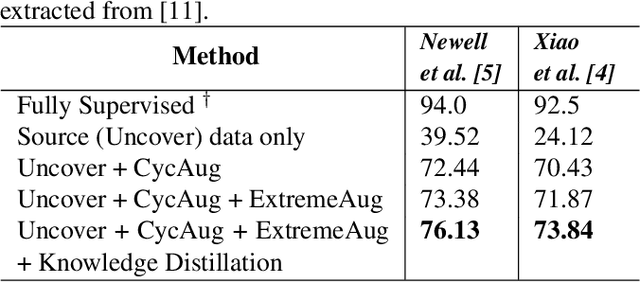
Human behavioral monitoring during sleep is essential for various medical applications. Majority of the contactless human pose estimation algorithms are based on RGB modality, causing ineffectiveness in in-bed pose estimation due to occlusions by blankets and varying illumination conditions. Long-wavelength infrared (LWIR) modality based pose estimation algorithms overcome the aforementioned challenges; however, ground truth pose generations by a human annotator under such conditions are not feasible. A feasible solution to address this issue is to transfer the knowledge learned from images with pose labels and no occlusions, and adapt it towards real world conditions (occlusions due to blankets). In this paper, we propose a novel learning strategy comprises of two-fold data augmentation to reduce the cross-domain discrepancy and knowledge distillation to learn the distribution of unlabeled images in real world conditions. Our experiments and analysis show the effectiveness of our approach over multiple standard human pose estimation baselines.

A Thickness Sensitive Vessel Extraction Framework for Retinal and Conjunctival Vascular Tortuosity Analysis

Systemic diseases such as diabetes, hypertension, atherosclerosis are among the leading causes of annual human mortality rate. It is suggested that retinal and conjunctival vascular tortuosity is a potential biomarker for such systemic diseases. Most importantly, it is observed that the tortuosity depends on the thickness of these vessels. Therefore, selective calculation of tortuosity within specific vessel thicknesses is required depending on the disease being analysed. In this paper, we propose a thickness sensitive vessel extraction framework that is primarily applicable for studies related to retinal and conjunctival vascular tortuosity. The framework uses a Convolutional Neural Network based on the IterNet architecture to obtain probability maps of the entire vasculature. They are then processed by a multi-scale vessel enhancement technique that exploits both fine and coarse structural vascular details of these probability maps in order to extract vessels of specified thicknesses. We evaluated the proposed framework on four datasets including DRIVE and SBVPI, and obtained Matthew's Correlation Coefficient values greater than 0.71 for all the datasets. In addition, the proposed framework was utilized to determine the association of diabetes with retinal and conjunctival vascular tortuosity. We observed that retinal vascular tortuosity (Eccentricity based Tortuosity Index) of the diabetic group was significantly higher (p < .05) than that of the non-diabetic group and that conjunctival vascular tortuosity (Total Curvature normalized by Arc Length) of diabetic group was significantly lower (p < .05) than that of the non-diabetic group. These observations were in agreement with the literature, strengthening the suitability of the proposed framework.

A Joint Convolutional and Spatial Quad-Directional LSTM Network for Phase Unwrapping

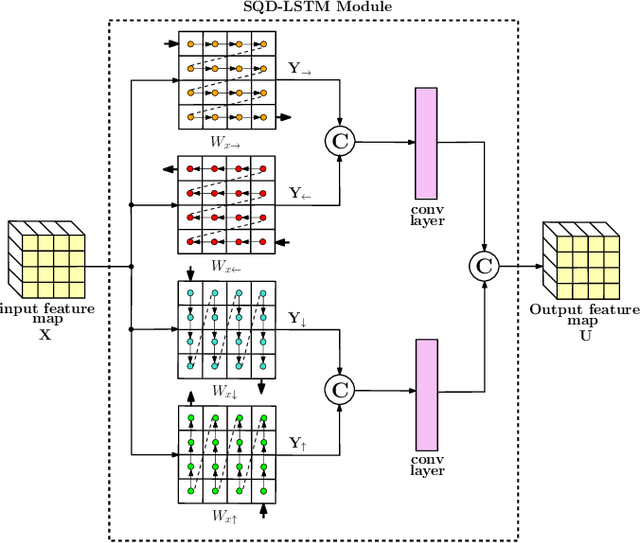
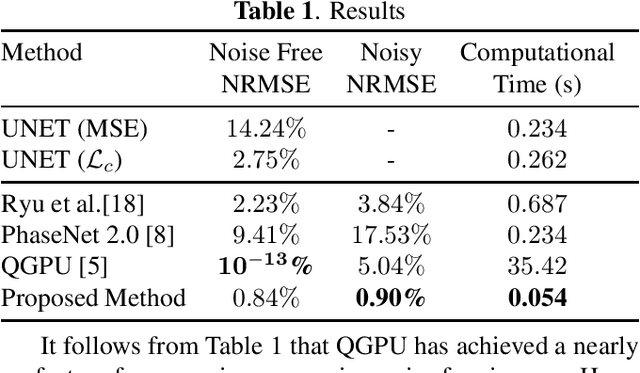
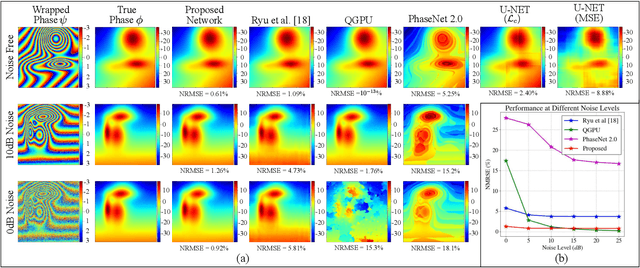
Phase unwrapping is a classical ill-posed problem which aims to recover the true phase from wrapped phase. In this paper, we introduce a novel Convolutional Neural Network (CNN) that incorporates a Spatial Quad-Directional Long Short Term Memory (SQD-LSTM) for phase unwrapping, by formulating it as a regression problem. Incorporating SQD-LSTM can circumvent the typical CNNs' inherent difficulty of learning global spatial dependencies which are vital when recovering the true phase. Furthermore, we employ a problem specific composite loss function to train this network. The proposed network is found to be performing better than the existing methods under severe noise conditions (Normalized Root Mean Square Error of 1.3 % at SNR = 0 dB) while spending a significantly less computational time (0.054 s). The network also does not require a large scale dataset during training, thus making it ideal for applications with limited data that require fast and accurate phase unwrapping.