Out-of-distribution and in-distribution posterior calibration using Kernel Density Polytopes

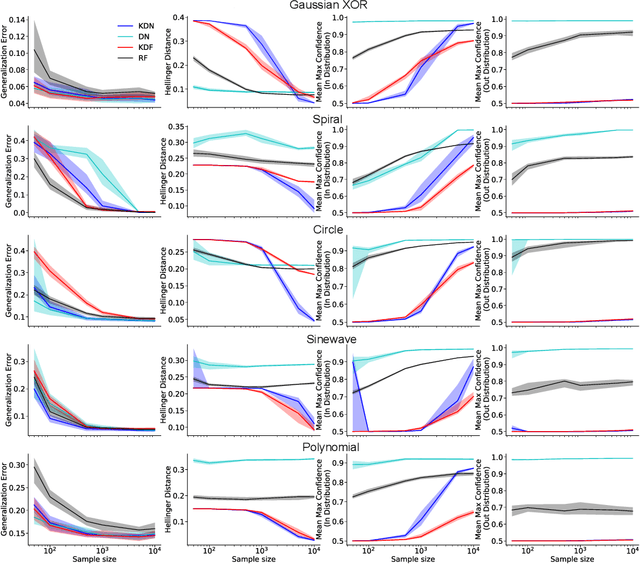
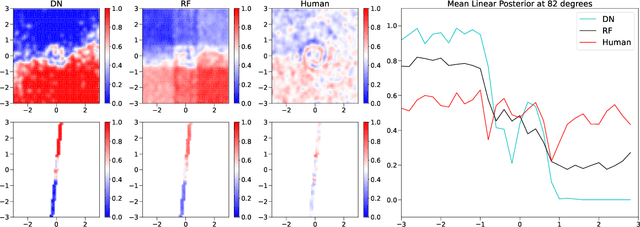
Any reasonable machine learning (ML) model should not only interpolate efficiently in between the training samples provided (in-distribution region), but also approach the extrapolative or out-of-distribution (OOD) region without being overconfident. Our experiment on human subjects justifies the aforementioned properties for human intelligence as well. Many state-of-the-art algorithms have tried to fix the overconfidence problem of ML models in the OOD region. However, in doing so, they have often impaired the in-distribution performance of the model. Our key insight is that ML models partition the feature space into polytopes and learn constant (random forests) or affine (ReLU networks) functions over those polytopes. This leads to the OOD overconfidence problem for the polytopes which lie in the training data boundary and extend to infinity. To resolve this issue, we propose kernel density methods that fit Gaussian kernel over the polytopes, which are learned using ML models. Specifically, we introduce two variants of kernel density polytopes: Kernel Density Forest (KDF) and Kernel Density Network (KDN) based on random forests and deep networks, respectively. Studies on various simulation settings show that both KDF and KDN achieve uniform confidence over the classes in the OOD region while maintaining good in-distribution accuracy compared to that of their respective parent models.

Streaming Decision Trees and Forests

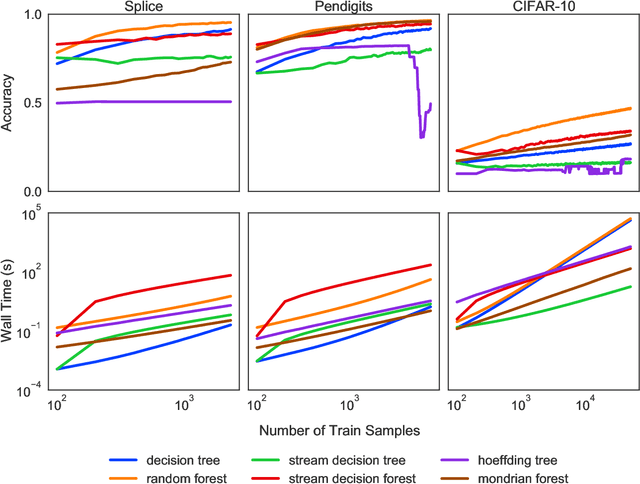
Machine learning has successfully leveraged modern data and provided computational solutions to innumerable real-world problems, including physical and biomedical discoveries. Currently, estimators could handle both scenarios with all samples available and situations requiring continuous updates. However, there is still room for improvement on streaming algorithms based on batch decision trees and random forests, which are the leading methods in batch data tasks. In this paper, we explore the simplest partial fitting algorithm to extend batch trees and test our models: stream decision tree (SDT) and stream decision forest (SDF) on three classification tasks of varying complexities. For reference, both existing streaming trees (Hoeffding trees and Mondrian forests) and batch estimators are included in the experiments. In all three tasks, SDF consistently produces high accuracy, whereas existing estimators encounter space restraints and accuracy fluctuations. Thus, our streaming trees and forests show great potential for further improvements, which are good candidates for solving problems like distribution drift and transfer learning.

When are Deep Networks really better than Random Forests at small sample sizes?

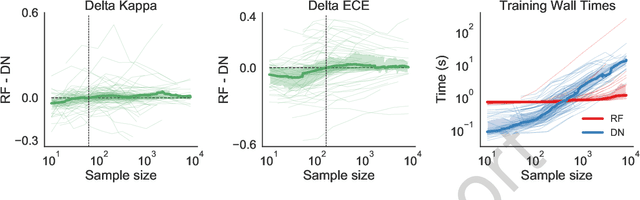
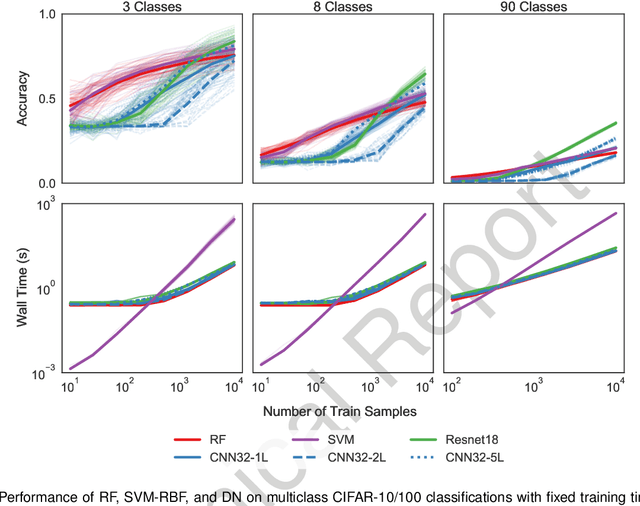
Random forests (RF) and deep networks (DN) are two of the most popular machine learning methods in the current scientific literature and yield differing levels of performance on different data modalities. We wish to further explore and establish the conditions and domains in which each approach excels, particularly in the context of sample size and feature dimension. To address these issues, we tested the performance of these approaches across tabular, image, and audio settings using varying model parameters and architectures. Our focus is on datasets with at most 10,000 samples, which represent a large fraction of scientific and biomedical datasets. In general, we found RF to excel at tabular and structured data (image and audio) with small sample sizes, whereas DN performed better on structured data with larger sample sizes. Although we plan to continue updating this technical report in the coming months, we believe the current preliminary results may be of interest to others.