Out-of-Distribution Detection & Applications With Ablated Learned Temperature Energy

As deep neural networks become adopted in high-stakes domains, it is crucial to be able to identify when inference inputs are Out-of-Distribution (OOD) so that users can be alerted of likely drops in performance and calibration despite high confidence. Among many others, existing methods use the following two scores to do so without training on any apriori OOD examples: a learned temperature and an energy score. In this paper we introduce Ablated Learned Temperature Energy (or "AbeT" for short), a method which combines these prior methods in novel ways with effective modifications. Due to these contributions, AbeT lowers the False Positive Rate at $95\%$ True Positive Rate (FPR@95) by $35.39\%$ in classification (averaged across all ID and OOD datasets measured) compared to state of the art without training networks in multiple stages or requiring hyperparameters or test-time backward passes. We additionally provide empirical insights as to how our model learns to distinguish between In-Distribution (ID) and OOD samples while only being explicitly trained on ID samples via exposure to misclassified ID examples at training time. Lastly, we show the efficacy of our method in identifying predicted bounding boxes and pixels corresponding to OOD objects in object detection and semantic segmentation, respectively - with an AUROC increase of $5.15\%$ in object detection and both a decrease in FPR@95 of $41.48\%$ and an increase in AUPRC of $34.20\%$ on average in semantic segmentation compared to previous state of the art.

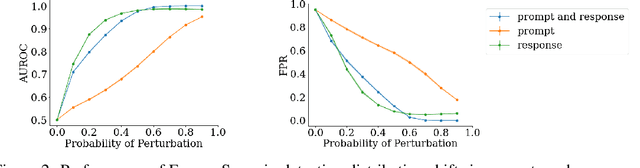
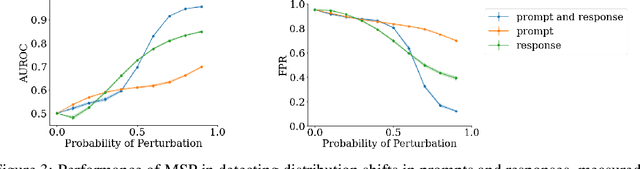
A Baseline Analysis of Reward Models' Ability To Accurately Analyze Foundation Models Under Distribution Shift

Foundation models, specifically Large Language Models (LLM's), have lately gained wide-spread attention and adoption. Reinforcement Learning with Human Feedback (RLHF) involves training a reward model to capture desired behaviors, which is then used to align LLM's. These reward models are additionally used at inference-time to estimate LLM responses' adherence to those desired behaviors. However, there is little work measuring how robust these reward models are to distribution shifts. In this work, we evaluate how reward model performance - measured via accuracy and calibration (i.e. alignment between accuracy and confidence) - is affected by distribution shift. We show novel calibration patterns and accuracy drops due to OOD prompts and responses, and that the reward model is more sensitive to shifts in responses than prompts. Additionally, we adapt an OOD detection technique commonly used in classification to the reward model setting to detect these distribution shifts in prompts and responses.

Enabling Calibration In The Zero-Shot Inference of Large Vision-Language Models

Calibration of deep learning models is crucial to their trustworthiness and safe usage, and as such, has been extensively studied in supervised classification models, with methods crafted to decrease miscalibration. However, there has yet to be a comprehensive study of the calibration of vision-language models that are used for zero-shot inference, like CLIP. We measure calibration across relevant variables like prompt, dataset, and architecture, and find that zero-shot inference with CLIP is miscalibrated. Furthermore, we propose a modified version of temperature scaling that is aligned with the common use cases of CLIP as a zero-shot inference model, and show that a single learned temperature generalizes for each specific CLIP model (defined by a chosen pre-training dataset and architecture) across inference dataset and prompt choice.

Out-of-distribution and in-distribution posterior calibration using Kernel Density Polytopes

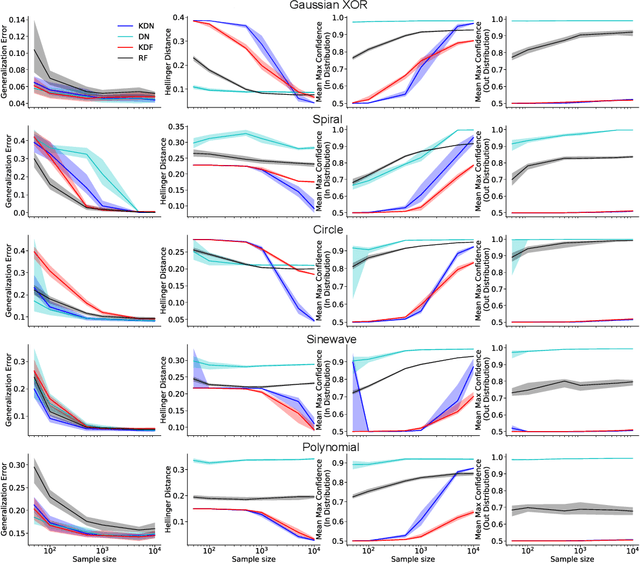
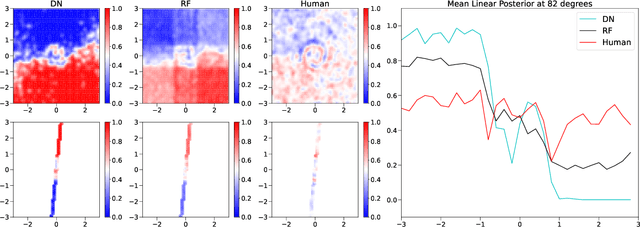
Any reasonable machine learning (ML) model should not only interpolate efficiently in between the training samples provided (in-distribution region), but also approach the extrapolative or out-of-distribution (OOD) region without being overconfident. Our experiment on human subjects justifies the aforementioned properties for human intelligence as well. Many state-of-the-art algorithms have tried to fix the overconfidence problem of ML models in the OOD region. However, in doing so, they have often impaired the in-distribution performance of the model. Our key insight is that ML models partition the feature space into polytopes and learn constant (random forests) or affine (ReLU networks) functions over those polytopes. This leads to the OOD overconfidence problem for the polytopes which lie in the training data boundary and extend to infinity. To resolve this issue, we propose kernel density methods that fit Gaussian kernel over the polytopes, which are learned using ML models. Specifically, we introduce two variants of kernel density polytopes: Kernel Density Forest (KDF) and Kernel Density Network (KDN) based on random forests and deep networks, respectively. Studies on various simulation settings show that both KDF and KDN achieve uniform confidence over the classes in the OOD region while maintaining good in-distribution accuracy compared to that of their respective parent models.

A general approach to progressive learning

In biological learning, data is used to improve performance on the task at hand, while simultaneously improving performance on both previously encountered tasks and as yet unconsidered future tasks. In contrast, classical machine learning starts from a blank slate, or tabula rasa, using data only for the single task at hand. While typical transfer learning algorithms can improve performance on future tasks, their performance degrades upon learning new tasks. Many recent approaches have attempted to mitigate this issue, called catastrophic forgetting, to maintain performance given new tasks. But striving to avoid forgetting sets the goal unnecessarily low: the goal of progressive learning, whether biological or artificial, is to improve performance on all tasks (including past and future) with any new data. We propose a general approach to progressive learning that ensembles representations, rather than learners. We show that ensembling representations---including representations learned by decision forests or neural networks---enables both forward and backward transfer on a variety of simulated and real data tasks, including vision, language, and adversarial tasks. This work suggests that further improvements in progressive learning may follow from a deeper understanding of how biological learning achieves such high degrees of efficiency.