Out-of-Distribution Detection & Applications With Ablated Learned Temperature Energy

As deep neural networks become adopted in high-stakes domains, it is crucial to be able to identify when inference inputs are Out-of-Distribution (OOD) so that users can be alerted of likely drops in performance and calibration despite high confidence. Among many others, existing methods use the following two scores to do so without training on any apriori OOD examples: a learned temperature and an energy score. In this paper we introduce Ablated Learned Temperature Energy (or "AbeT" for short), a method which combines these prior methods in novel ways with effective modifications. Due to these contributions, AbeT lowers the False Positive Rate at $95\%$ True Positive Rate (FPR@95) by $35.39\%$ in classification (averaged across all ID and OOD datasets measured) compared to state of the art without training networks in multiple stages or requiring hyperparameters or test-time backward passes. We additionally provide empirical insights as to how our model learns to distinguish between In-Distribution (ID) and OOD samples while only being explicitly trained on ID samples via exposure to misclassified ID examples at training time. Lastly, we show the efficacy of our method in identifying predicted bounding boxes and pixels corresponding to OOD objects in object detection and semantic segmentation, respectively - with an AUROC increase of $5.15\%$ in object detection and both a decrease in FPR@95 of $41.48\%$ and an increase in AUPRC of $34.20\%$ on average in semantic segmentation compared to previous state of the art.

Enabling Calibration In The Zero-Shot Inference of Large Vision-Language Models

Calibration of deep learning models is crucial to their trustworthiness and safe usage, and as such, has been extensively studied in supervised classification models, with methods crafted to decrease miscalibration. However, there has yet to be a comprehensive study of the calibration of vision-language models that are used for zero-shot inference, like CLIP. We measure calibration across relevant variables like prompt, dataset, and architecture, and find that zero-shot inference with CLIP is miscalibrated. Furthermore, we propose a modified version of temperature scaling that is aligned with the common use cases of CLIP as a zero-shot inference model, and show that a single learned temperature generalizes for each specific CLIP model (defined by a chosen pre-training dataset and architecture) across inference dataset and prompt choice.

Control Variates for Slate Off-Policy Evaluation

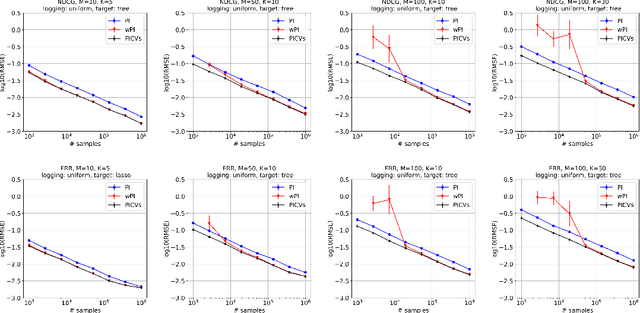
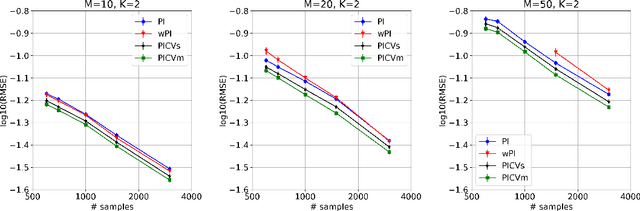
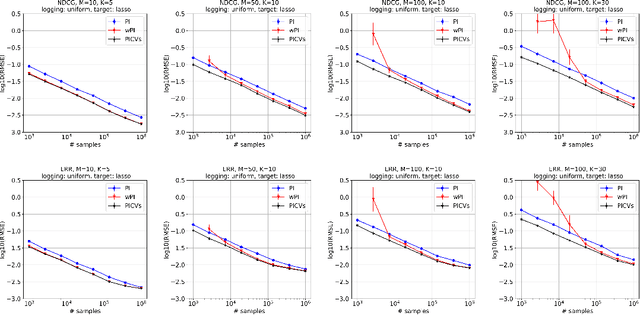
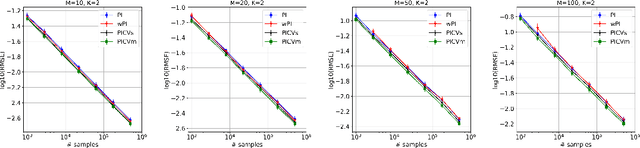
We study the problem of off-policy evaluation from batched contextual bandit data with multidimensional actions, often termed slates. The problem is common to recommender systems and user-interface optimization, and it is particularly challenging because of the combinatorially-sized action space. Swaminathan et al. (2017) have proposed the pseudoinverse (PI) estimator under the assumption that the conditional mean rewards are additive in actions. Using control variates, we consider a large class of unbiased estimators that includes as specific cases the PI estimator and (asymptotically) its self-normalized variant. By optimizing over this class, we obtain new estimators with risk improvement guarantees over both the PI and self-normalized PI estimators. Experiments with real-world recommender data as well as synthetic data validate these improvements in practice.

Off-Policy Evaluation of Slate Policies under Bayes Risk

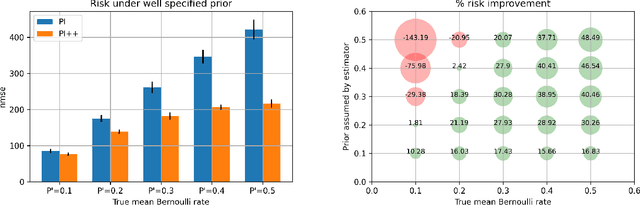
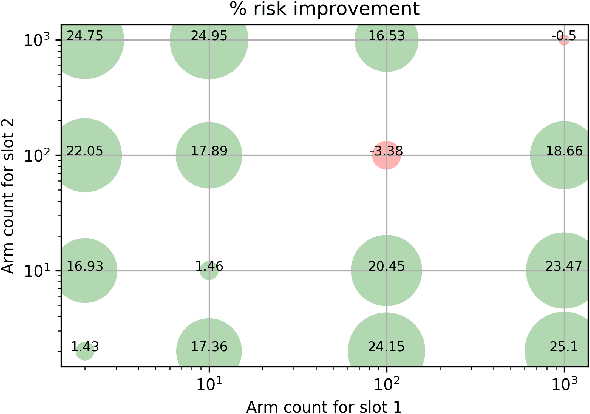
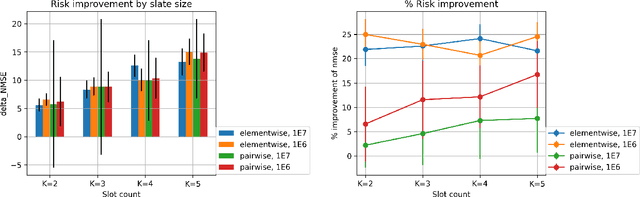
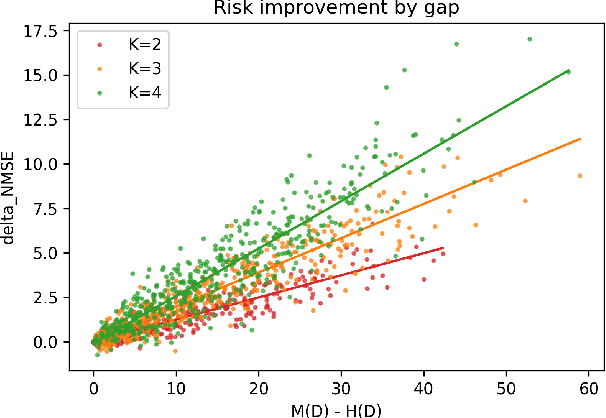
We study the problem of off-policy evaluation for slate bandits, for the typical case in which the logging policy factorizes over the slots of the slate. We slightly depart from the existing literature by taking Bayes risk as the criterion by which to evaluate estimators, and we analyze the family of 'additive' estimators that includes the pseudoinverse (PI) estimator of Swaminathan et al.\ (2017; arXiv:1605.04812). Using a control variate approach, we identify a new estimator in this family that is guaranteed to have lower risk than PI in the above class of problems. In particular, we show that the risk improvement over PI grows linearly with the number of slots, and linearly with the gap between the arithmetic and the harmonic mean of a set of slot-level divergences between the logging and the target policy. In the typical case of a uniform logging policy and a deterministic target policy, each divergence corresponds to slot size, showing that maximal gains can be obtained for slate problems with diverse numbers of actions per slot.