Out-of-distribution and in-distribution posterior calibration using Kernel Density Polytopes

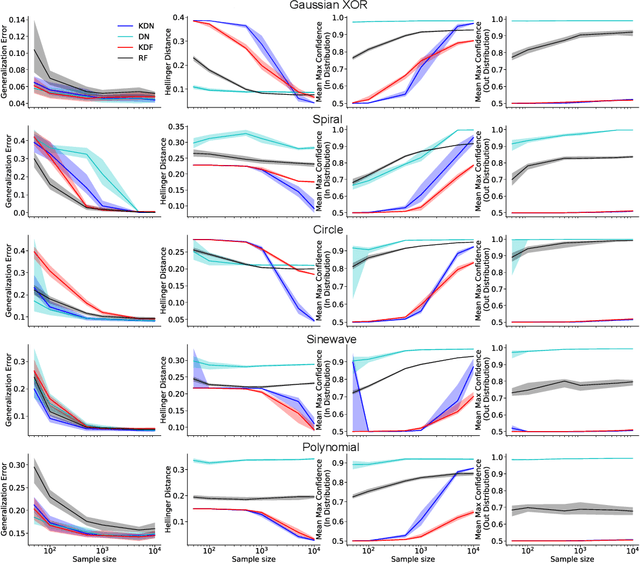
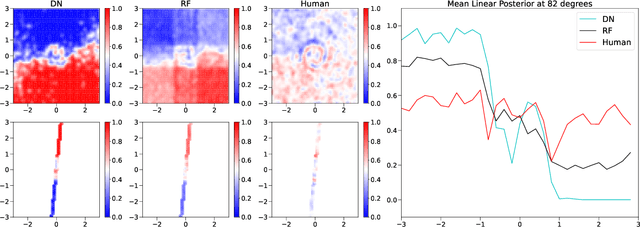
Any reasonable machine learning (ML) model should not only interpolate efficiently in between the training samples provided (in-distribution region), but also approach the extrapolative or out-of-distribution (OOD) region without being overconfident. Our experiment on human subjects justifies the aforementioned properties for human intelligence as well. Many state-of-the-art algorithms have tried to fix the overconfidence problem of ML models in the OOD region. However, in doing so, they have often impaired the in-distribution performance of the model. Our key insight is that ML models partition the feature space into polytopes and learn constant (random forests) or affine (ReLU networks) functions over those polytopes. This leads to the OOD overconfidence problem for the polytopes which lie in the training data boundary and extend to infinity. To resolve this issue, we propose kernel density methods that fit Gaussian kernel over the polytopes, which are learned using ML models. Specifically, we introduce two variants of kernel density polytopes: Kernel Density Forest (KDF) and Kernel Density Network (KDN) based on random forests and deep networks, respectively. Studies on various simulation settings show that both KDF and KDN achieve uniform confidence over the classes in the OOD region while maintaining good in-distribution accuracy compared to that of their respective parent models.

Prospective Learning: Back to the Future

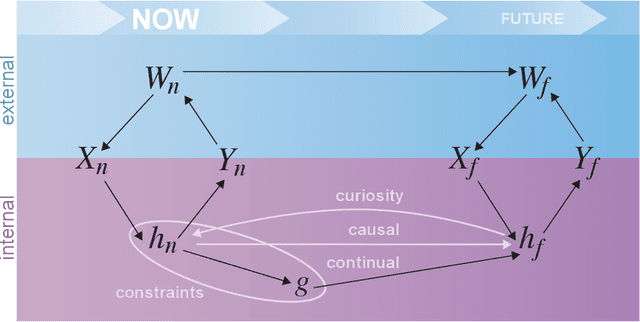
Research on both natural intelligence (NI) and artificial intelligence (AI) generally assumes that the future resembles the past: intelligent agents or systems (what we call 'intelligence') observe and act on the world, then use this experience to act on future experiences of the same kind. We call this 'retrospective learning'. For example, an intelligence may see a set of pictures of objects, along with their names, and learn to name them. A retrospective learning intelligence would merely be able to name more pictures of the same objects. We argue that this is not what true intelligence is about. In many real world problems, both NIs and AIs will have to learn for an uncertain future. Both must update their internal models to be useful for future tasks, such as naming fundamentally new objects and using these objects effectively in a new context or to achieve previously unencountered goals. This ability to learn for the future we call 'prospective learning'. We articulate four relevant factors that jointly define prospective learning. Continual learning enables intelligences to remember those aspects of the past which it believes will be most useful in the future. Prospective constraints (including biases and priors) facilitate the intelligence finding general solutions that will be applicable to future problems. Curiosity motivates taking actions that inform future decision making, including in previously unmet situations. Causal estimation enables learning the structure of relations that guide choosing actions for specific outcomes, even when the specific action-outcome contingencies have never been observed before. We argue that a paradigm shift from retrospective to prospective learning will enable the communities that study intelligence to unite and overcome existing bottlenecks to more effectively explain, augment, and engineer intelligences.