Optimal Transport with Cyclic Symmetry

We propose novel fast algorithms for optimal transport (OT) utilizing a cyclic symmetry structure of input data. Such OT with cyclic symmetry appears universally in various real-world examples: image processing, urban planning, and graph processing. Our main idea is to reduce OT to a small optimization problem that has significantly fewer variables by utilizing cyclic symmetry and various optimization techniques. On the basis of this reduction, our algorithms solve the small optimization problem instead of the original OT. As a result, our algorithms obtain the optimal solution and the objective function value of the original OT faster than solving the original OT directly. In this paper, our focus is on two crucial OT formulations: the linear programming OT (LOT) and the strongly convex-regularized OT, which includes the well-known entropy-regularized OT (EROT). Experiments show the effectiveness of our algorithms for LOT and EROT in synthetic/real-world data that has a strict/approximate cyclic symmetry structure. Through theoretical and experimental results, this paper successfully introduces the concept of symmetry into the OT research field for the first time.

Non-approximate Inference for Collective Graphical Models on Path Graphs via Discrete Difference of Convex Algorithm

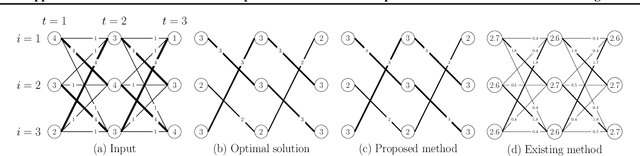
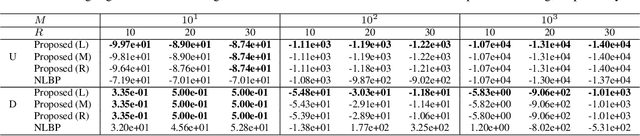
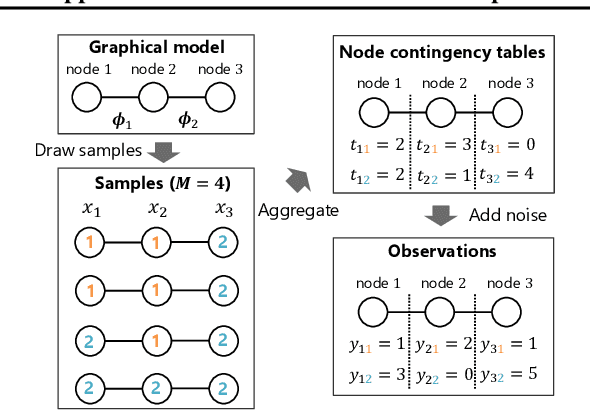
The importance of aggregated count data, which is calculated from the data of multiple individuals, continues to increase. Collective Graphical Model (CGM) is a probabilistic approach to the analysis of aggregated data. One of the most important operations in CGM is maximum a posteriori (MAP) inference of unobserved variables under given observations. Because the MAP inference problem for general CGMs has been shown to be NP-hard, an approach that solves an approximate problem has been proposed. However, this approach has two major drawbacks. First, the quality of the solution deteriorates when the values in the count tables are small, because the approximation becomes inaccurate. Second, since continuous relaxation is applied, the integrality constraints of the output are violated. To resolve these problems, this paper proposes a new method for MAP inference for CGMs on path graphs. First we show that the MAP inference problem can be formulated as a (non-linear) minimum cost flow problem. Then, we apply Difference of Convex Algorithm (DCA), which is a general methodology to minimize a function represented as the sum of a convex function and a concave function. In our algorithm, important subroutines in DCA can be efficiently calculated by minimum convex cost flow algorithms. Experiments show that the proposed method outputs higher quality solutions than the conventional approach.