Deep Positive-Unlabeled Anomaly Detection for Contaminated Unlabeled Data

Semi-supervised anomaly detection, which aims to improve the performance of the anomaly detector by using a small amount of anomaly data in addition to unlabeled data, has attracted attention. Existing semi-supervised approaches assume that unlabeled data are mostly normal. They train the anomaly detector to minimize the anomaly scores for the unlabeled data, and to maximize those for the anomaly data. However, in practice, the unlabeled data are often contaminated with anomalies. This weakens the effect of maximizing the anomaly scores for anomalies, and prevents us from improving the detection performance. To solve this problem, we propose the positive-unlabeled autoencoder, which is based on positive-unlabeled learning and the anomaly detector such as the autoencoder. With our approach, we can approximate the anomaly scores for normal data using the unlabeled and anomaly data. Therefore, without the labeled normal data, we can train the anomaly detector to minimize the anomaly scores for normal data, and to maximize those for the anomaly data. In addition, our approach is applicable to various anomaly detectors such as the DeepSVDD. Experiments on various datasets show that our approach achieves better detection performance than existing approaches.

Switching One-Versus-the-Rest Loss to Increase the Margin of Logits for Adversarial Robustness

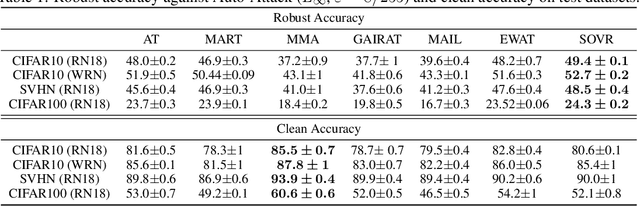
Defending deep neural networks against adversarial examples is a key challenge for AI safety. To improve the robustness effectively, recent methods focus on important data points near the decision boundary in adversarial training. However, these methods are vulnerable to Auto-Attack, which is an ensemble of parameter-free attacks for reliable evaluation. In this paper, we experimentally investigate the causes of their vulnerability and find that existing methods reduce margins between logits for the true label and the other labels while keeping their gradient norms non-small values. Reduced margins and non-small gradient norms cause their vulnerability since the largest logit can be easily flipped by the perturbation. Our experiments also show that the histogram of the logit margins has two peaks, i.e., small and large logit margins. From the observations, we propose switching one-versus-the-rest loss (SOVR), which uses one-versus-the-rest loss when data have small logit margins so that it increases the margins. We find that SOVR increases logit margins more than existing methods while keeping gradient norms small and outperforms them in terms of the robustness against Auto-Attack.

Smoothness Analysis of Loss Functions of Adversarial Training

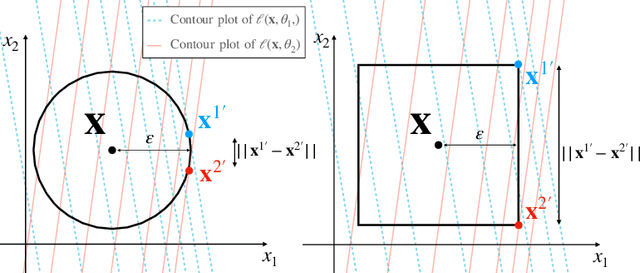
Deep neural networks are vulnerable to adversarial attacks. Recent studies of adversarial robustness focus on the loss landscape in the parameter space since it is related to optimization performance. These studies conclude that it is hard to optimize the loss function for adversarial training with respect to parameters because the loss function is not smooth: i.e., its gradient is not Lipschitz continuous. However, this analysis ignores the dependence of adversarial attacks on parameters. Since adversarial attacks are the worst noise for the models, they should depend on the parameters of the models. In this study, we analyze the smoothness of the loss function of adversarial training for binary linear classification considering the dependence. We reveal that the Lipschitz continuity depends on the types of constraints of adversarial attacks in this case. Specifically, under the L2 constraints, the adversarial loss is smooth except at zero.

Adversarial Training Makes Weight Loss Landscape Sharper in Logistic Regression

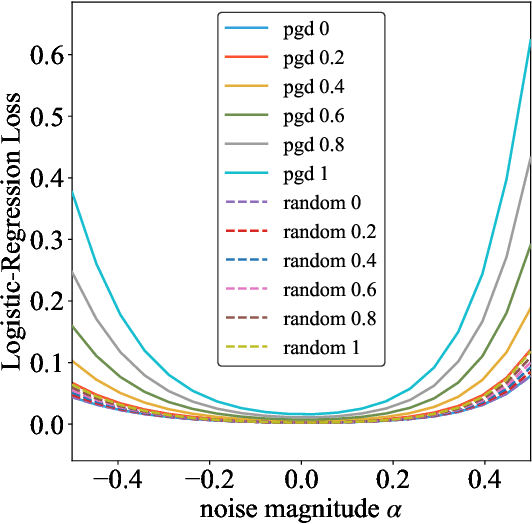
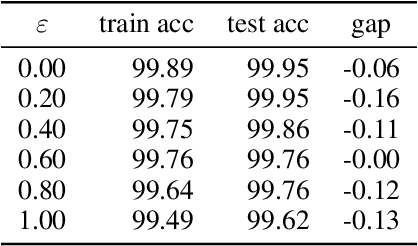
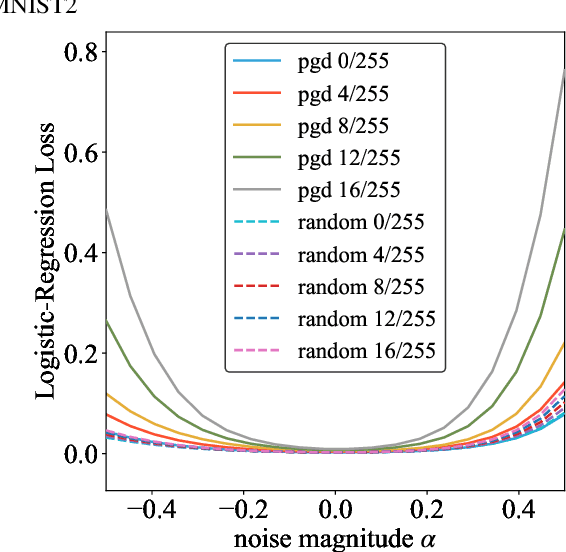
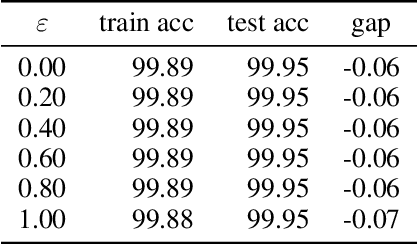
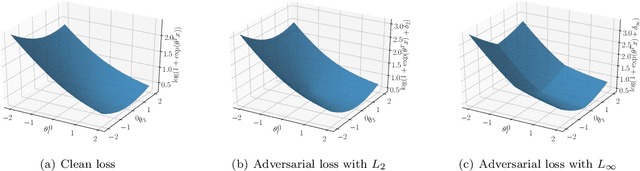
Adversarial training is actively studied for learning robust models against adversarial examples. A recent study finds that adversarially trained models degenerate generalization performance on adversarial examples when their weight loss landscape, which is loss changes with respect to weights, is sharp. Unfortunately, it has been experimentally shown that adversarial training sharpens the weight loss landscape, but this phenomenon has not been theoretically clarified. Therefore, we theoretically analyze this phenomenon in this paper. As a first step, this paper proves that adversarial training with the L2 norm constraints sharpens the weight loss landscape in the linear logistic regression model. Our analysis reveals that the sharpness of the weight loss landscape is caused by the noise aligned in the direction of increasing the loss, which is used in adversarial training. We theoretically and experimentally confirm that the weight loss landscape becomes sharper as the magnitude of the noise of adversarial training increases in the linear logistic regression model. Moreover, we experimentally confirm the same phenomena in ResNet18 with softmax as a more general case.

Constraining Logits by Bounded Function for Adversarial Robustness

We propose a method for improving adversarial robustness by addition of a new bounded function just before softmax. Recent studies hypothesize that small logits (inputs of softmax) by logit regularization can improve adversarial robustness of deep learning. Following this hypothesis, we analyze norms of logit vectors at the optimal point under the assumption of universal approximation and explore new methods for constraining logits by addition of a bounded function before softmax. We theoretically and empirically reveal that small logits by addition of a common activation function, e.g., hyperbolic tangent, do not improve adversarial robustness since input vectors of the function (pre-logit vectors) can have large norms. From the theoretical findings, we develop the new bounded function. The addition of our function improves adversarial robustness because it makes logit and pre-logit vectors have small norms. Since our method only adds one activation function before softmax, it is easy to combine our method with adversarial training. Our experiments demonstrate that our method is comparable to logit regularization methods in terms of accuracies on adversarially perturbed datasets without adversarial training. Furthermore, it is superior or comparable to logit regularization methods and a recent defense method (TRADES) when using adversarial training.

Autoencoding Binary Classifiers for Supervised Anomaly Detection

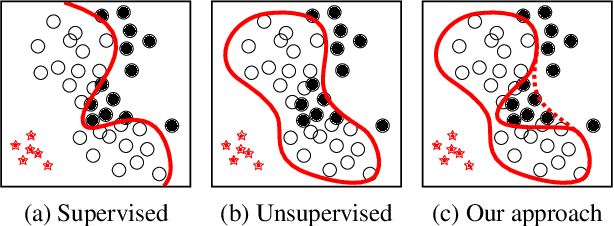
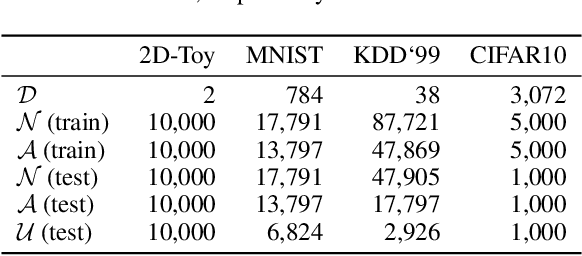
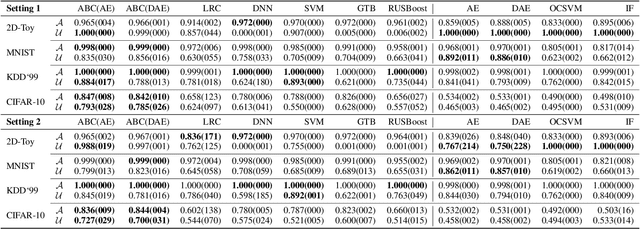
We propose the Autoencoding Binary Classifiers (ABC), a novel supervised anomaly detector based on the Autoencoder (AE). There are two main approaches in anomaly detection: supervised and unsupervised. The supervised approach accurately detects the known anomalies included in training data, but it cannot detect the unknown anomalies. Meanwhile, the unsupervised approach can detect both known and unknown anomalies that are located away from normal data points. However, it does not detect known anomalies as accurately as the supervised approach. Furthermore, even if we have labeled normal data points and anomalies, the unsupervised approach cannot utilize these labels. The ABC is a probabilistic binary classifier that effectively exploits the label information, where normal data points are modeled using the AE as a component. By maximizing the likelihood, the AE in the proposed ABC is trained to minimize the reconstruction error for normal data points, and to maximize it for known anomalies. Since our approach becomes able to reconstruct the normal data points accurately and fails to reconstruct the known and unknown anomalies, it can accurately discriminate both known and unknown anomalies from normal data points. Experimental results show that the ABC achieves higher detection performance than existing supervised and unsupervised methods.

Variational Autoencoder with Implicit Optimal Priors

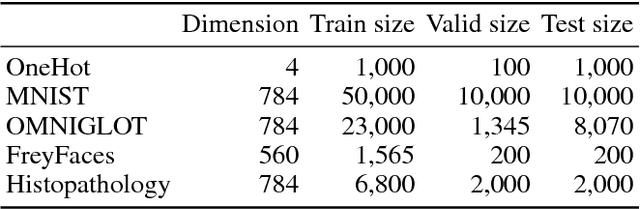
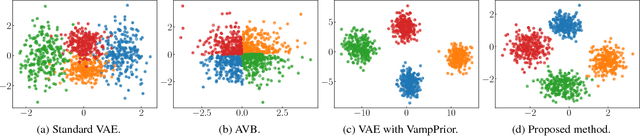
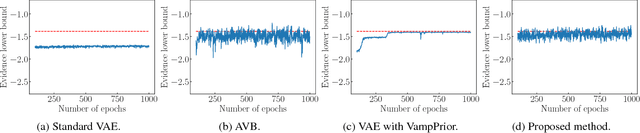
The variational autoencoder (VAE) is a powerful generative model that can estimate the probability of a data point by using latent variables. In the VAE, the posterior of the latent variable given the data point is regularized by the prior of the latent variable using Kullback Leibler (KL) divergence. Although the standard Gaussian distribution is usually used for the prior, this simple prior incurs over-regularization. As a sophisticated prior, the aggregated posterior has been introduced, which is the expectation of the posterior over the data distribution. This prior is optimal for the VAE in terms of maximizing the training objective function. However, KL divergence with the aggregated posterior cannot be calculated in a closed form, which prevents us from using this optimal prior. With the proposed method, we introduce the density ratio trick to estimate this KL divergence without modeling the aggregated posterior explicitly. Since the density ratio trick does not work well in high dimensions, we rewrite this KL divergence that contains the high-dimensional density ratio into the sum of the analytically calculable term and the low-dimensional density ratio term, to which the density ratio trick is applied. Experiments on various datasets show that the VAE with this implicit optimal prior achieves high density estimation performance.