Sekitoshi Kanai
Test-Time Alignment of LLMs via Sampling-Based Optimal Control in pre-logit space
Oct 30, 2025Abstract:Test-time alignment of large language models (LLMs) attracts attention because fine-tuning LLMs requires high computational costs. In this paper, we propose a new test-time alignment method called adaptive importance sampling on pre-logits (AISP) on the basis of the sampling-based model predictive control with the stochastic control input. AISP applies the Gaussian perturbation into pre-logits, which are outputs of the penultimate layer, so as to maximize expected rewards with respect to the mean of the perturbation. We demonstrate that the optimal mean is obtained by importance sampling with sampled rewards. AISP outperforms best-of-n sampling in terms of rewards over the number of used samples and achieves higher rewards than other reward-based test-time alignment methods.
Post-pre-training for Modality Alignment in Vision-Language Foundation Models
Apr 17, 2025
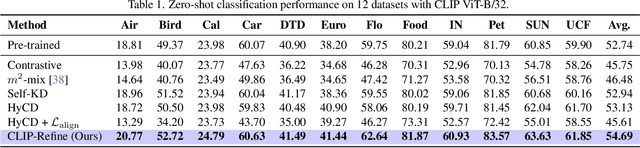
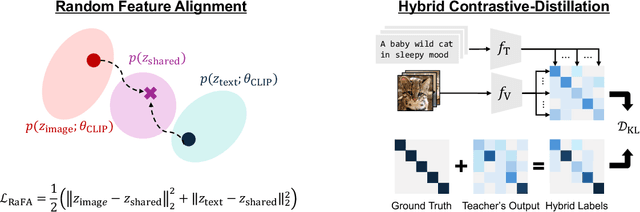
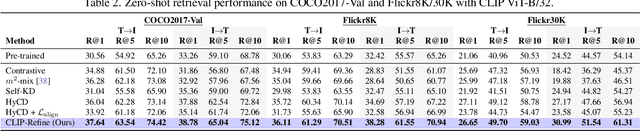
Abstract:Contrastive language image pre-training (CLIP) is an essential component of building modern vision-language foundation models. While CLIP demonstrates remarkable zero-shot performance on downstream tasks, the multi-modal feature spaces still suffer from a modality gap, which is a gap between image and text feature clusters and limits downstream task performance. Although existing works attempt to address the modality gap by modifying pre-training or fine-tuning, they struggle with heavy training costs with large datasets or degradations of zero-shot performance. This paper presents CLIP-Refine, a post-pre-training method for CLIP models at a phase between pre-training and fine-tuning. CLIP-Refine aims to align the feature space with 1 epoch training on small image-text datasets without zero-shot performance degradations. To this end, we introduce two techniques: random feature alignment (RaFA) and hybrid contrastive-distillation (HyCD). RaFA aligns the image and text features to follow a shared prior distribution by minimizing the distance to random reference vectors sampled from the prior. HyCD updates the model with hybrid soft labels generated by combining ground-truth image-text pair labels and outputs from the pre-trained CLIP model. This contributes to achieving both maintaining the past knowledge and learning new knowledge to align features. Our extensive experiments with multiple classification and retrieval tasks show that CLIP-Refine succeeds in mitigating the modality gap and improving the zero-shot performance.
Evaluating Time-Series Training Dataset through Lens of Spectrum in Deep State Space Models
Aug 29, 2024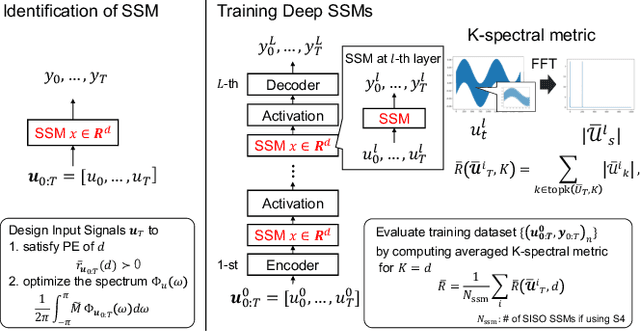

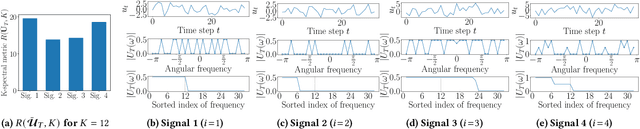
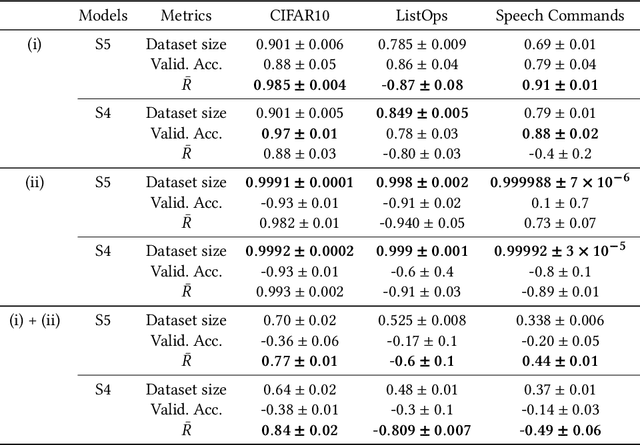
Abstract:This study investigates a method to evaluate time-series datasets in terms of the performance of deep neural networks (DNNs) with state space models (deep SSMs) trained on the dataset. SSMs have attracted attention as components inside DNNs to address time-series data. Since deep SSMs have powerful representation capacities, training datasets play a crucial role in solving a new task. However, the effectiveness of training datasets cannot be known until deep SSMs are actually trained on them. This can increase the cost of data collection for new tasks, as a trial-and-error process of data collection and time-consuming training are needed to achieve the necessary performance. To advance the practical use of deep SSMs, the metric of datasets to estimate the performance early in the training can be one key element. To this end, we introduce the concept of data evaluation methods used in system identification. In system identification of linear dynamical systems, the effectiveness of datasets is evaluated by using the spectrum of input signals. We introduce this concept to deep SSMs, which are nonlinear dynamical systems. We propose the K-spectral metric, which is the sum of the top-K spectra of signals inside deep SSMs, by focusing on the fact that each layer of a deep SSM can be regarded as a linear dynamical system. Our experiments show that the K-spectral metric has a large absolute value of the correlation coefficient with the performance and can be used to evaluate the quality of training datasets.
Adaptive Random Feature Regularization on Fine-tuning Deep Neural Networks
Mar 15, 2024Abstract:While fine-tuning is a de facto standard method for training deep neural networks, it still suffers from overfitting when using small target datasets. Previous methods improve fine-tuning performance by maintaining knowledge of the source datasets or introducing regularization terms such as contrastive loss. However, these methods require auxiliary source information (e.g., source labels or datasets) or heavy additional computations. In this paper, we propose a simple method called adaptive random feature regularization (AdaRand). AdaRand helps the feature extractors of training models to adaptively change the distribution of feature vectors for downstream classification tasks without auxiliary source information and with reasonable computation costs. To this end, AdaRand minimizes the gap between feature vectors and random reference vectors that are sampled from class conditional Gaussian distributions. Furthermore, AdaRand dynamically updates the conditional distribution to follow the currently updated feature extractors and balance the distance between classes in feature spaces. Our experiments show that AdaRand outperforms the other fine-tuning regularization, which requires auxiliary source information and heavy computation costs.
Adversarial Finetuning with Latent Representation Constraint to Mitigate Accuracy-Robustness Tradeoff
Aug 31, 2023



Abstract:This paper addresses the tradeoff between standard accuracy on clean examples and robustness against adversarial examples in deep neural networks (DNNs). Although adversarial training (AT) improves robustness, it degrades the standard accuracy, thus yielding the tradeoff. To mitigate this tradeoff, we propose a novel AT method called ARREST, which comprises three components: (i) adversarial finetuning (AFT), (ii) representation-guided knowledge distillation (RGKD), and (iii) noisy replay (NR). AFT trains a DNN on adversarial examples by initializing its parameters with a DNN that is standardly pretrained on clean examples. RGKD and NR respectively entail a regularization term and an algorithm to preserve latent representations of clean examples during AFT. RGKD penalizes the distance between the representations of the standardly pretrained and AFT DNNs. NR switches input adversarial examples to nonadversarial ones when the representation changes significantly during AFT. By combining these components, ARREST achieves both high standard accuracy and robustness. Experimental results demonstrate that ARREST mitigates the tradeoff more effectively than previous AT-based methods do.
Regularizing Neural Networks with Meta-Learning Generative Models
Jul 26, 2023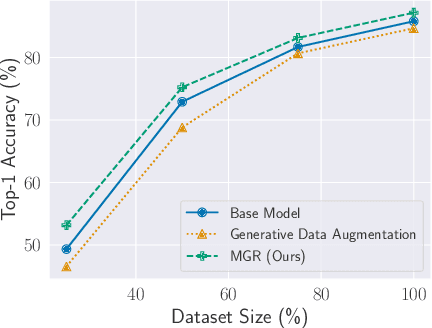

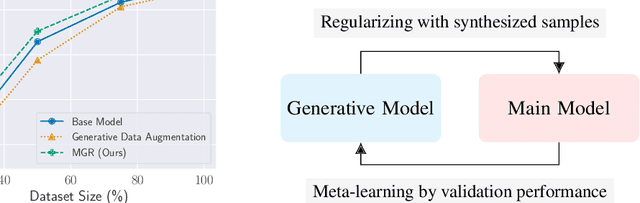

Abstract:This paper investigates methods for improving generative data augmentation for deep learning. Generative data augmentation leverages the synthetic samples produced by generative models as an additional dataset for classification with small dataset settings. A key challenge of generative data augmentation is that the synthetic data contain uninformative samples that degrade accuracy. This is because the synthetic samples do not perfectly represent class categories in real data and uniform sampling does not necessarily provide useful samples for tasks. In this paper, we present a novel strategy for generative data augmentation called meta generative regularization (MGR). To avoid the degradation of generative data augmentation, MGR utilizes synthetic samples in the regularization term for feature extractors instead of in the loss function, e.g., cross-entropy. These synthetic samples are dynamically determined to minimize the validation losses through meta-learning. We observed that MGR can avoid the performance degradation of na\"ive generative data augmentation and boost the baselines. Experiments on six datasets showed that MGR is effective particularly when datasets are smaller and stably outperforms baselines.
Fast Regularized Discrete Optimal Transport with Group-Sparse Regularizers
Mar 14, 2023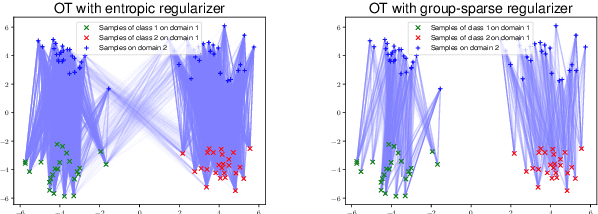
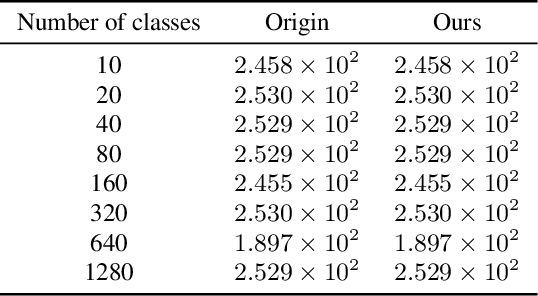
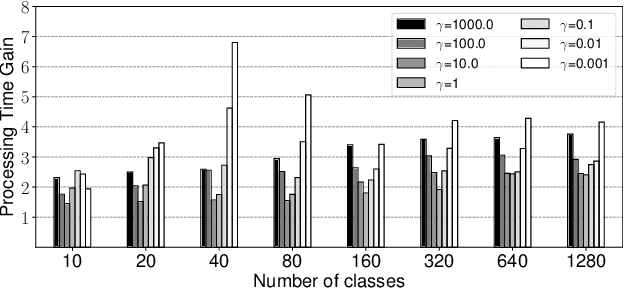
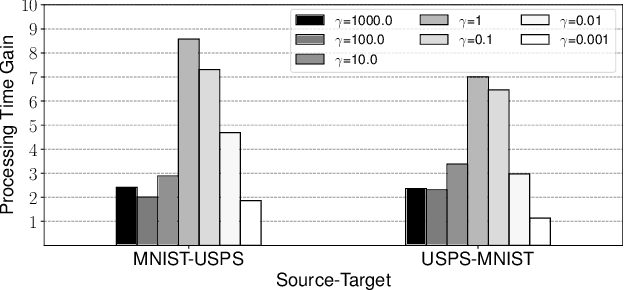
Abstract:Regularized discrete optimal transport (OT) is a powerful tool to measure the distance between two discrete distributions that have been constructed from data samples on two different domains. While it has a wide range of applications in machine learning, in some cases the sampled data from only one of the domains will have class labels such as unsupervised domain adaptation. In this kind of problem setting, a group-sparse regularizer is frequently leveraged as a regularization term to handle class labels. In particular, it can preserve the label structure on the data samples by corresponding the data samples with the same class label to one group-sparse regularization term. As a result, we can measure the distance while utilizing label information by solving the regularized optimization problem with gradient-based algorithms. However, the gradient computation is expensive when the number of classes or data samples is large because the number of regularization terms and their respective sizes also turn out to be large. This paper proposes fast discrete OT with group-sparse regularizers. Our method is based on two ideas. The first is to safely skip the computations of the gradients that must be zero. The second is to efficiently extract the gradients that are expected to be nonzero. Our method is guaranteed to return the same value of the objective function as that of the original method. Experiments show that our method is up to 8.6 times faster than the original method without degrading accuracy.
Fast Saturating Gate for Learning Long Time Scales with Recurrent Neural Networks
Oct 04, 2022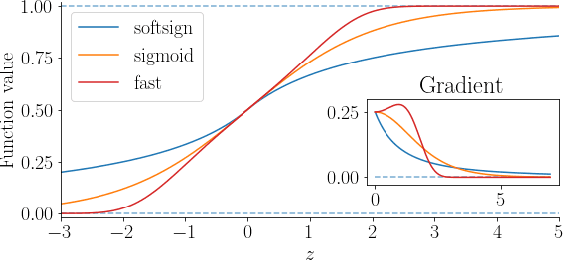

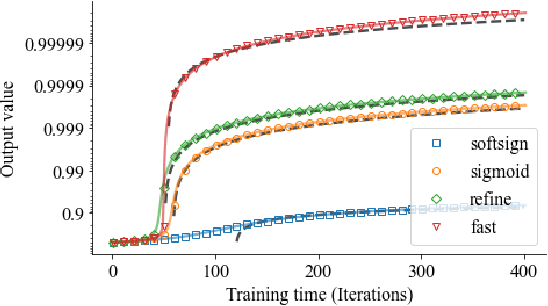
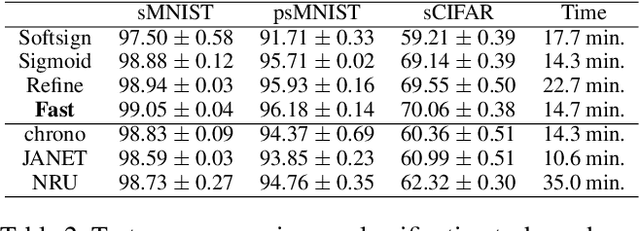
Abstract:Gate functions in recurrent models, such as an LSTM and GRU, play a central role in learning various time scales in modeling time series data by using a bounded activation function. However, it is difficult to train gates to capture extremely long time scales due to gradient vanishing of the bounded function for large inputs, which is known as the saturation problem. We closely analyze the relation between saturation of the gate function and efficiency of the training. We prove that the gradient vanishing of the gate function can be mitigated by accelerating the convergence of the saturating function, i.e., making the output of the function converge to 0 or 1 faster. Based on the analysis results, we propose a gate function called fast gate that has a doubly exponential convergence rate with respect to inputs by simple function composition. We empirically show that our method outperforms previous methods in accuracy and computational efficiency on benchmark tasks involving extremely long time scales.
Switching One-Versus-the-Rest Loss to Increase the Margin of Logits for Adversarial Robustness
Jul 21, 2022
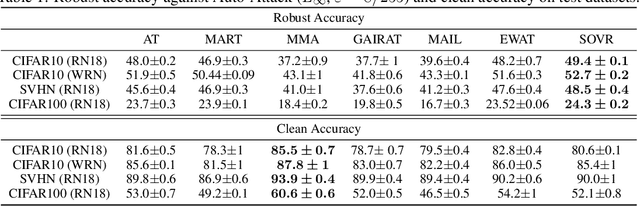


Abstract:Defending deep neural networks against adversarial examples is a key challenge for AI safety. To improve the robustness effectively, recent methods focus on important data points near the decision boundary in adversarial training. However, these methods are vulnerable to Auto-Attack, which is an ensemble of parameter-free attacks for reliable evaluation. In this paper, we experimentally investigate the causes of their vulnerability and find that existing methods reduce margins between logits for the true label and the other labels while keeping their gradient norms non-small values. Reduced margins and non-small gradient norms cause their vulnerability since the largest logit can be easily flipped by the perturbation. Our experiments also show that the histogram of the logit margins has two peaks, i.e., small and large logit margins. From the observations, we propose switching one-versus-the-rest loss (SOVR), which uses one-versus-the-rest loss when data have small logit margins so that it increases the margins. We find that SOVR increases logit margins more than existing methods while keeping gradient norms small and outperforms them in terms of the robustness against Auto-Attack.
Transfer Learning with Pre-trained Conditional Generative Models
Apr 27, 2022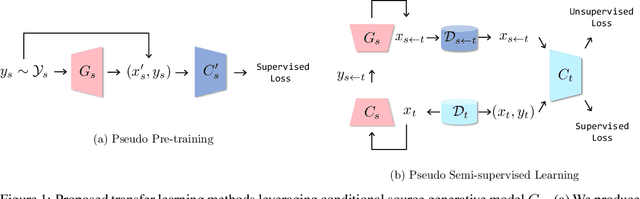

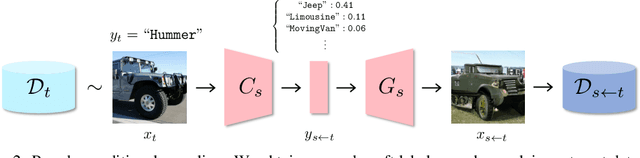
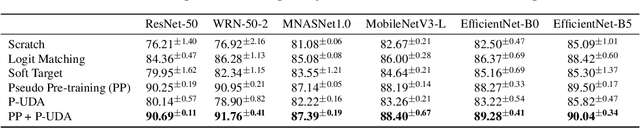
Abstract:Transfer learning is crucial in training deep neural networks on new target tasks. Current transfer learning methods generally assume at least one of (i) source and target task label spaces must overlap, (ii) source datasets are available, and (iii) target network architectures are consistent with source ones. However, these all assumptions are difficult to hold in practical settings because the target task rarely has the same labels as the source task, the source dataset access is restricted due to licensing and storage costs, and the target architecture is often specialized to each task. To transfer source knowledge without these assumptions, we propose a transfer learning method that uses deep generative models and is composed of the following two stages: pseudo pre-training (PP) and pseudo semi-supervised learning (P-SSL). PP trains a target architecture with a synthesized dataset by using conditional source generative models. P-SSL applies SSL algorithms to labeled target data and unlabeled pseudo samples, which are generated by cascading the source classifier and generative models to condition them with target samples. Our experimental results indicate that our method can outperform baselines of scratch training and knowledge distillation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge