Atsutoshi Kumagai
Do We Really Need Permutations? Impact of Width Expansion on Linear Mode Connectivity
Oct 09, 2025Abstract:Recently, Ainsworth et al. empirically demonstrated that, given two independently trained models, applying a parameter permutation that preserves the input-output behavior allows the two models to be connected by a low-loss linear path. When such a path exists, the models are said to achieve linear mode connectivity (LMC). Prior studies, including Ainsworth et al., have reported that achieving LMC requires not only an appropriate permutation search but also sufficiently wide models (e.g., a 32 $\times$ width multiplier for ResNet-20). This is broadly believed to be because increasing the model width ensures a large enough space of candidate permutations, increasing the chance of finding one that yields LMC. In this work, we empirically demonstrate that, even without any permutations, simply widening the models is sufficient for achieving LMC when using a suitable softmax temperature calibration. We further explain why this phenomenon arises by analyzing intermediate layer outputs. Specifically, we introduce layerwise exponentially weighted connectivity (LEWC), which states that the output of each layer of the merged model can be represented as an exponentially weighted sum of the outputs of the corresponding layers of the original models. Consequently the merged model's output matches that of an ensemble of the original models, which facilitates LMC. To the best of our knowledge, this work is the first to show that widening the model not only facilitates nonlinear mode connectivity, as suggested in prior research, but also significantly increases the possibility of achieving linear mode connectivity.
Meta-learning Representations for Learning from Multiple Annotators
Jun 12, 2025Abstract:We propose a meta-learning method for learning from multiple noisy annotators. In many applications such as crowdsourcing services, labels for supervised learning are given by multiple annotators. Since the annotators have different skills or biases, given labels can be noisy. To learn accurate classifiers, existing methods require many noisy annotated data. However, sufficient data might be unavailable in practice. To overcome the lack of data, the proposed method uses labeled data obtained in different but related tasks. The proposed method embeds each example in tasks to a latent space by using a neural network and constructs a probabilistic model for learning a task-specific classifier while estimating annotators' abilities on the latent space. This neural network is meta-learned to improve the expected test classification performance when the classifier is adapted to a given small amount of annotated data. This classifier adaptation is performed by maximizing the posterior probability via the expectation-maximization (EM) algorithm. Since each step in the EM algorithm is easily computed as a closed-form and is differentiable, the proposed method can efficiently backpropagate the loss through the EM algorithm to meta-learn the neural network. We show the effectiveness of our method with real-world datasets with synthetic noise and real-world crowdsourcing datasets.
Positive-Unlabeled Diffusion Models for Preventing Sensitive Data Generation
Mar 05, 2025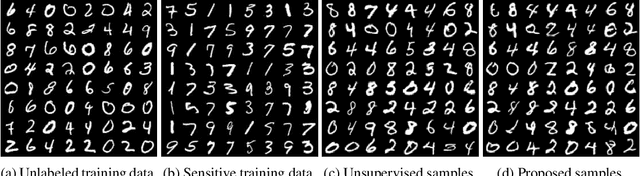
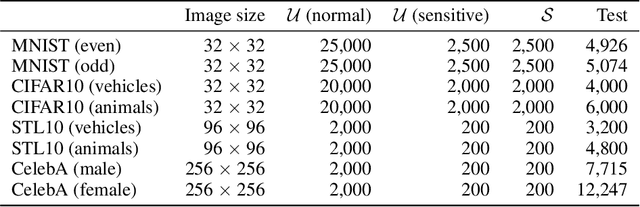
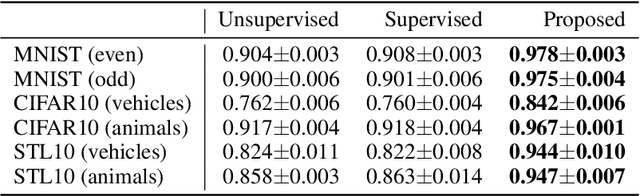

Abstract:Diffusion models are powerful generative models but often generate sensitive data that are unwanted by users, mainly because the unlabeled training data frequently contain such sensitive data. Since labeling all sensitive data in the large-scale unlabeled training data is impractical, we address this problem by using a small amount of labeled sensitive data. In this paper, we propose positive-unlabeled diffusion models, which prevent the generation of sensitive data using unlabeled and sensitive data. Our approach can approximate the evidence lower bound (ELBO) for normal (negative) data using only unlabeled and sensitive (positive) data. Therefore, even without labeled normal data, we can maximize the ELBO for normal data and minimize it for labeled sensitive data, ensuring the generation of only normal data. Through experiments across various datasets and settings, we demonstrated that our approach can prevent the generation of sensitive images without compromising image quality.
Test-time Adaptation for Regression by Subspace Alignment
Oct 04, 2024Abstract:This paper investigates test-time adaptation (TTA) for regression, where a regression model pre-trained in a source domain is adapted to an unknown target distribution with unlabeled target data. Although regression is one of the fundamental tasks in machine learning, most of the existing TTA methods have classification-specific designs, which assume that models output class-categorical predictions, whereas regression models typically output only single scalar values. To enable TTA for regression, we adopt a feature alignment approach, which aligns the feature distributions between the source and target domains to mitigate the domain gap. However, we found that naive feature alignment employed in existing TTA methods for classification is ineffective or even worse for regression because the features are distributed in a small subspace and many of the raw feature dimensions have little significance to the output. For an effective feature alignment in TTA for regression, we propose Significant-subspace Alignment (SSA). SSA consists of two components: subspace detection and dimension weighting. Subspace detection finds the feature subspace that is representative and significant to the output. Then, the feature alignment is performed in the subspace during TTA. Meanwhile, dimension weighting raises the importance of the dimensions of the feature subspace that have greater significance to the output. We experimentally show that SSA outperforms various baselines on real-world datasets.
Meta-learning for Positive-unlabeled Classification
Jun 06, 2024



Abstract:We propose a meta-learning method for positive and unlabeled (PU) classification, which improves the performance of binary classifiers obtained from only PU data in unseen target tasks. PU learning is an important problem since PU data naturally arise in real-world applications such as outlier detection and information retrieval. Existing PU learning methods require many PU data, but sufficient data are often unavailable in practice. The proposed method minimizes the test classification risk after the model is adapted to PU data by using related tasks that consist of positive, negative, and unlabeled data. We formulate the adaptation as an estimation problem of the Bayes optimal classifier, which is an optimal classifier to minimize the classification risk. The proposed method embeds each instance into a task-specific space using neural networks. With the embedded PU data, the Bayes optimal classifier is estimated through density-ratio estimation of PU densities, whose solution is obtained as a closed-form solution. The closed-form solution enables us to efficiently and effectively minimize the test classification risk. We empirically show that the proposed method outperforms existing methods with one synthetic and three real-world datasets.
Deep Positive-Unlabeled Anomaly Detection for Contaminated Unlabeled Data
May 29, 2024Abstract:Semi-supervised anomaly detection, which aims to improve the performance of the anomaly detector by using a small amount of anomaly data in addition to unlabeled data, has attracted attention. Existing semi-supervised approaches assume that unlabeled data are mostly normal. They train the anomaly detector to minimize the anomaly scores for the unlabeled data, and to maximize those for the anomaly data. However, in practice, the unlabeled data are often contaminated with anomalies. This weakens the effect of maximizing the anomaly scores for anomalies, and prevents us from improving the detection performance. To solve this problem, we propose the positive-unlabeled autoencoder, which is based on positive-unlabeled learning and the anomaly detector such as the autoencoder. With our approach, we can approximate the anomaly scores for normal data using the unlabeled and anomaly data. Therefore, without the labeled normal data, we can train the anomaly detector to minimize the anomaly scores for normal data, and to maximize those for the anomaly data. In addition, our approach is applicable to various anomaly detectors such as the DeepSVDD. Experiments on various datasets show that our approach achieves better detection performance than existing approaches.
Analysis of Linear Mode Connectivity via Permutation-Based Weight Matching
Feb 19, 2024Abstract:Recently, Ainsworth et al. showed that using weight matching (WM) to minimize the $L_2$ distance in a permutation search of model parameters effectively identifies permutations that satisfy linear mode connectivity (LMC), in which the loss along a linear path between two independently trained models with different seeds remains nearly constant. This paper provides a theoretical analysis of LMC using WM, which is crucial for understanding stochastic gradient descent's effectiveness and its application in areas like model merging. We first experimentally and theoretically show that permutations found by WM do not significantly reduce the $L_2$ distance between two models and the occurrence of LMC is not merely due to distance reduction by WM in itself. We then provide theoretical insights showing that permutations can change the directions of the singular vectors, but not the singular values, of the weight matrices in each layer. This finding shows that permutations found by WM mainly align the directions of singular vectors associated with large singular values across models. This alignment brings the singular vectors with large singular values, which determine the model functionality, closer between pre-merged and post-merged models, so that the post-merged model retains functionality similar to the pre-merged models, making it easy to satisfy LMC. Finally, we analyze the difference between WM and straight-through estimator (STE), a dataset-dependent permutation search method, and show that WM outperforms STE, especially when merging three or more models.
Meta-learning to Calibrate Gaussian Processes with Deep Kernels for Regression Uncertainty Estimation
Dec 13, 2023Abstract:Although Gaussian processes (GPs) with deep kernels have been successfully used for meta-learning in regression tasks, its uncertainty estimation performance can be poor. We propose a meta-learning method for calibrating deep kernel GPs for improving regression uncertainty estimation performance with a limited number of training data. The proposed method meta-learns how to calibrate uncertainty using data from various tasks by minimizing the test expected calibration error, and uses the knowledge for unseen tasks. We design our model such that the adaptation and calibration for each task can be performed without iterative procedures, which enables effective meta-learning. In particular, a task-specific uncalibrated output distribution is modeled by a GP with a task-shared encoder network, and it is transformed to a calibrated one using a cumulative density function of a task-specific Gaussian mixture model (GMM). By integrating the GP and GMM into our neural network-based model, we can meta-learn model parameters in an end-to-end fashion. Our experiments demonstrate that the proposed method improves uncertainty estimation performance while keeping high regression performance compared with the existing methods using real-world datasets in few-shot settings.
Meta-learning of semi-supervised learning from tasks with heterogeneous attribute spaces
Nov 09, 2023Abstract:We propose a meta-learning method for semi-supervised learning that learns from multiple tasks with heterogeneous attribute spaces. The existing semi-supervised meta-learning methods assume that all tasks share the same attribute space, which prevents us from learning with a wide variety of tasks. With the proposed method, the expected test performance on tasks with a small amount of labeled data is improved with unlabeled data as well as data in various tasks, where the attribute spaces are different among tasks. The proposed method embeds labeled and unlabeled data simultaneously in a task-specific space using a neural network, and the unlabeled data's labels are estimated by adapting classification or regression models in the embedding space. For the neural network, we develop variable-feature self-attention layers, which enable us to find embeddings of data with different attribute spaces with a single neural network by considering interactions among examples, attributes, and labels. Our experiments on classification and regression datasets with heterogeneous attribute spaces demonstrate that our proposed method outperforms the existing meta-learning and semi-supervised learning methods.
Regularizing Neural Networks with Meta-Learning Generative Models
Jul 26, 2023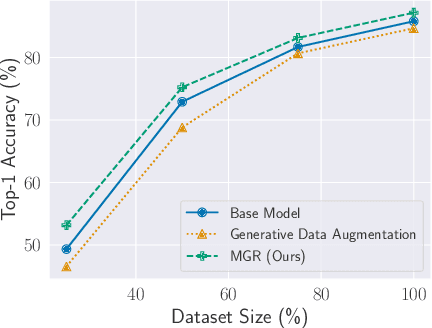

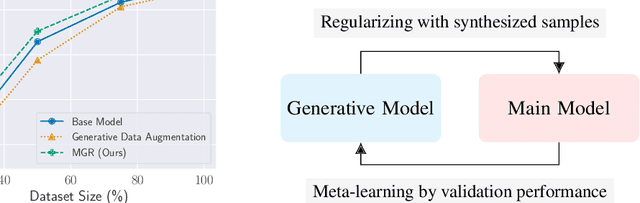

Abstract:This paper investigates methods for improving generative data augmentation for deep learning. Generative data augmentation leverages the synthetic samples produced by generative models as an additional dataset for classification with small dataset settings. A key challenge of generative data augmentation is that the synthetic data contain uninformative samples that degrade accuracy. This is because the synthetic samples do not perfectly represent class categories in real data and uniform sampling does not necessarily provide useful samples for tasks. In this paper, we present a novel strategy for generative data augmentation called meta generative regularization (MGR). To avoid the degradation of generative data augmentation, MGR utilizes synthetic samples in the regularization term for feature extractors instead of in the loss function, e.g., cross-entropy. These synthetic samples are dynamically determined to minimize the validation losses through meta-learning. We observed that MGR can avoid the performance degradation of na\"ive generative data augmentation and boost the baselines. Experiments on six datasets showed that MGR is effective particularly when datasets are smaller and stably outperforms baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge