Test-time Adaptation for Regression by Subspace Alignment
Paper and Code
Oct 04, 2024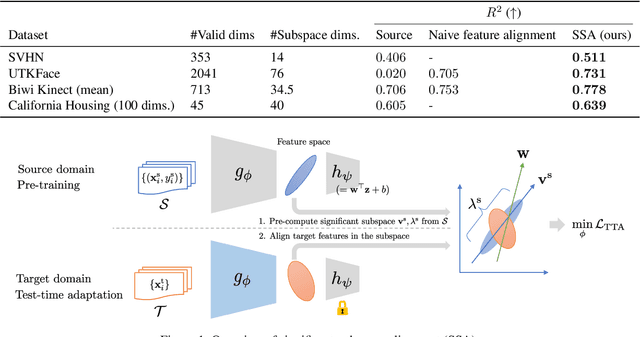
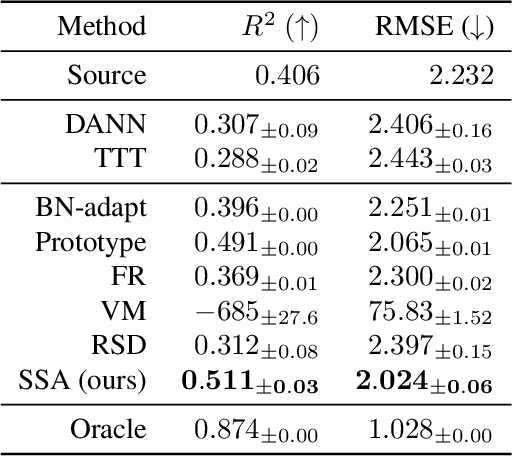
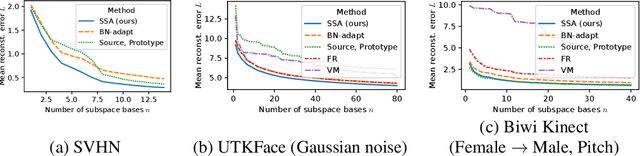
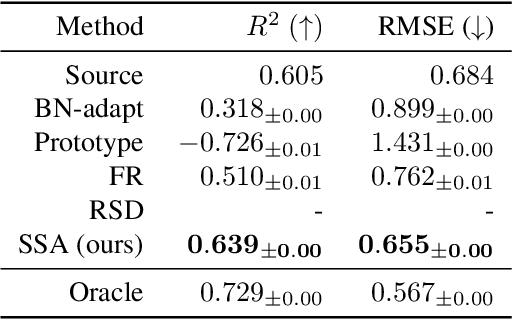
This paper investigates test-time adaptation (TTA) for regression, where a regression model pre-trained in a source domain is adapted to an unknown target distribution with unlabeled target data. Although regression is one of the fundamental tasks in machine learning, most of the existing TTA methods have classification-specific designs, which assume that models output class-categorical predictions, whereas regression models typically output only single scalar values. To enable TTA for regression, we adopt a feature alignment approach, which aligns the feature distributions between the source and target domains to mitigate the domain gap. However, we found that naive feature alignment employed in existing TTA methods for classification is ineffective or even worse for regression because the features are distributed in a small subspace and many of the raw feature dimensions have little significance to the output. For an effective feature alignment in TTA for regression, we propose Significant-subspace Alignment (SSA). SSA consists of two components: subspace detection and dimension weighting. Subspace detection finds the feature subspace that is representative and significant to the output. Then, the feature alignment is performed in the subspace during TTA. Meanwhile, dimension weighting raises the importance of the dimensions of the feature subspace that have greater significance to the output. We experimentally show that SSA outperforms various baselines on real-world datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge