Evaluating Time-Series Training Dataset through Lens of Spectrum in Deep State Space Models
Paper and Code
Aug 29, 2024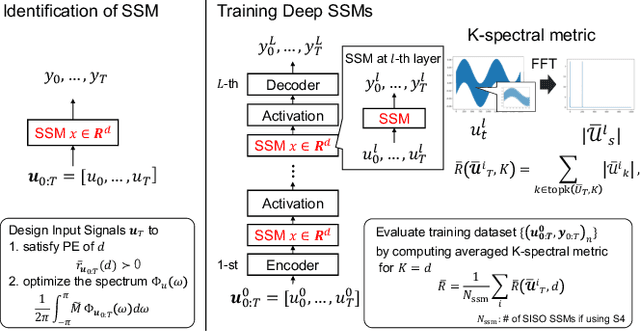

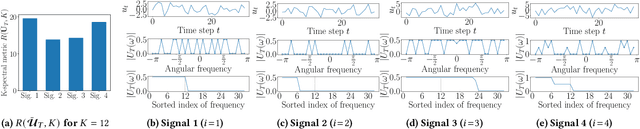
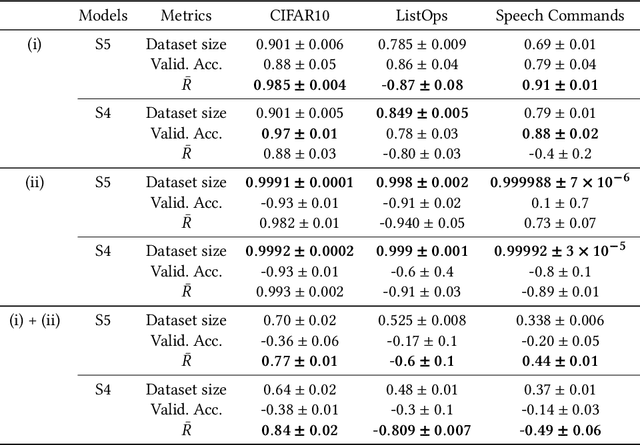
This study investigates a method to evaluate time-series datasets in terms of the performance of deep neural networks (DNNs) with state space models (deep SSMs) trained on the dataset. SSMs have attracted attention as components inside DNNs to address time-series data. Since deep SSMs have powerful representation capacities, training datasets play a crucial role in solving a new task. However, the effectiveness of training datasets cannot be known until deep SSMs are actually trained on them. This can increase the cost of data collection for new tasks, as a trial-and-error process of data collection and time-consuming training are needed to achieve the necessary performance. To advance the practical use of deep SSMs, the metric of datasets to estimate the performance early in the training can be one key element. To this end, we introduce the concept of data evaluation methods used in system identification. In system identification of linear dynamical systems, the effectiveness of datasets is evaluated by using the spectrum of input signals. We introduce this concept to deep SSMs, which are nonlinear dynamical systems. We propose the K-spectral metric, which is the sum of the top-K spectra of signals inside deep SSMs, by focusing on the fact that each layer of a deep SSM can be regarded as a linear dynamical system. Our experiments show that the K-spectral metric has a large absolute value of the correlation coefficient with the performance and can be used to evaluate the quality of training datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge