Test-Time Alignment of LLMs via Sampling-Based Optimal Control in pre-logit space

Test-time alignment of large language models (LLMs) attracts attention because fine-tuning LLMs requires high computational costs. In this paper, we propose a new test-time alignment method called adaptive importance sampling on pre-logits (AISP) on the basis of the sampling-based model predictive control with the stochastic control input. AISP applies the Gaussian perturbation into pre-logits, which are outputs of the penultimate layer, so as to maximize expected rewards with respect to the mean of the perturbation. We demonstrate that the optimal mean is obtained by importance sampling with sampled rewards. AISP outperforms best-of-n sampling in terms of rewards over the number of used samples and achieves higher rewards than other reward-based test-time alignment methods.

Empirical Bayes Estimation for Lasso-Type Regularizers: Analysis of Automatic Relevance Determination

This paper focuses on linear regression models with non-conjugate sparsity-inducing regularizers such as lasso and group lasso. Although empirical Bayes approach enables us to estimate the regularization parameter, little is known on the properties of the estimators. In particular, there are many unexplained aspects regarding the specific conditions under which the mechanism of automatic relevance determination (ARD) occurs. In this paper, we derive the empirical Bayes estimators for the group lasso regularized linear regression models with a limited number of parameters. It is shown that the estimators diverge under a certain condition, giving rise to the ARD mechanism. We also prove that empirical Bayes methods can produce ARD mechanism in general regularized linear regression models and clarify the conditions under which models such as ridge, lasso, and group lasso can produce ARD mechanism.

Evaluating Time-Series Training Dataset through Lens of Spectrum in Deep State Space Models

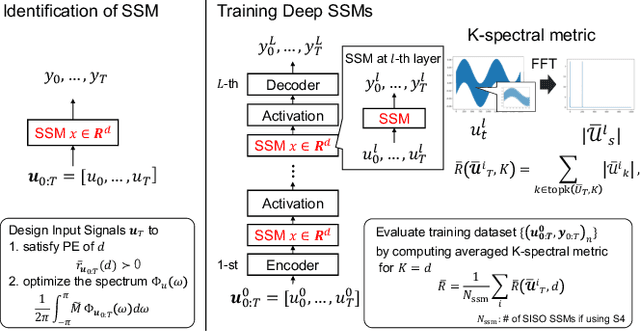
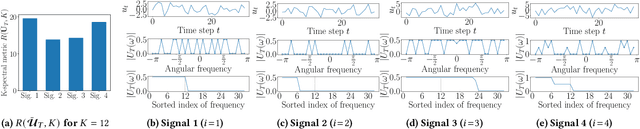
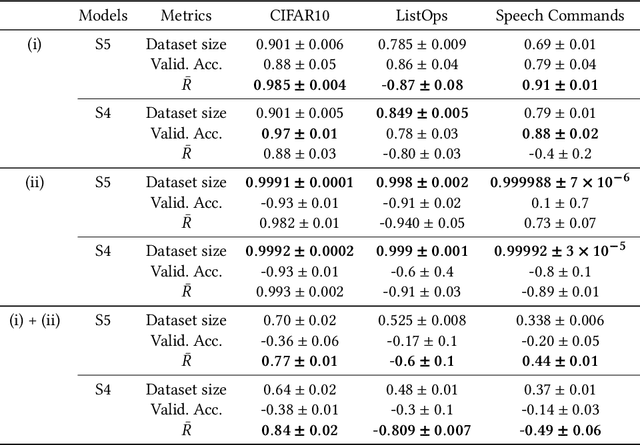
This study investigates a method to evaluate time-series datasets in terms of the performance of deep neural networks (DNNs) with state space models (deep SSMs) trained on the dataset. SSMs have attracted attention as components inside DNNs to address time-series data. Since deep SSMs have powerful representation capacities, training datasets play a crucial role in solving a new task. However, the effectiveness of training datasets cannot be known until deep SSMs are actually trained on them. This can increase the cost of data collection for new tasks, as a trial-and-error process of data collection and time-consuming training are needed to achieve the necessary performance. To advance the practical use of deep SSMs, the metric of datasets to estimate the performance early in the training can be one key element. To this end, we introduce the concept of data evaluation methods used in system identification. In system identification of linear dynamical systems, the effectiveness of datasets is evaluated by using the spectrum of input signals. We introduce this concept to deep SSMs, which are nonlinear dynamical systems. We propose the K-spectral metric, which is the sum of the top-K spectra of signals inside deep SSMs, by focusing on the fact that each layer of a deep SSM can be regarded as a linear dynamical system. Our experiments show that the K-spectral metric has a large absolute value of the correlation coefficient with the performance and can be used to evaluate the quality of training datasets.