Empirical Bayes Estimation for Lasso-Type Regularizers: Analysis of Automatic Relevance Determination

This paper focuses on linear regression models with non-conjugate sparsity-inducing regularizers such as lasso and group lasso. Although empirical Bayes approach enables us to estimate the regularization parameter, little is known on the properties of the estimators. In particular, there are many unexplained aspects regarding the specific conditions under which the mechanism of automatic relevance determination (ARD) occurs. In this paper, we derive the empirical Bayes estimators for the group lasso regularized linear regression models with a limited number of parameters. It is shown that the estimators diverge under a certain condition, giving rise to the ARD mechanism. We also prove that empirical Bayes methods can produce ARD mechanism in general regularized linear regression models and clarify the conditions under which models such as ridge, lasso, and group lasso can produce ARD mechanism.

Unbiased Estimating Equation on Inverse Divergence and Its Conditions

This paper focuses on the Bregman divergence defined by the reciprocal function, called the inverse divergence. For the loss function defined by the monotonically increasing function $f$ and inverse divergence, the conditions for the statistical model and function $f$ under which the estimating equation is unbiased are clarified. Specifically, we characterize two types of statistical models, an inverse Gaussian type and a mixture of generalized inverse Gaussian type distributions, to show that the conditions for the function $f$ are different for each model. We also define Bregman divergence as a linear sum over the dimensions of the inverse divergence and extend the results to the multi-dimensional case.

Unified Likelihood Ratio Estimation for High- to Zero-frequency N-grams

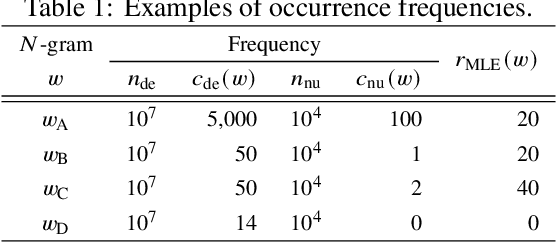
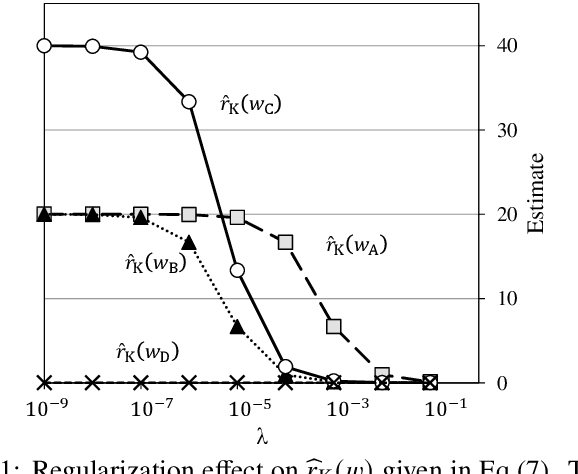
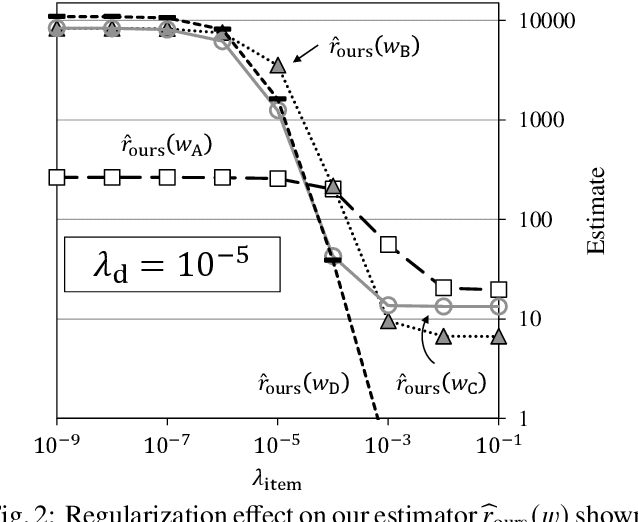
Likelihood ratios (LRs), which are commonly used for probabilistic data processing, are often estimated based on the frequency counts of individual elements obtained from samples. In natural language processing, an element can be a continuous sequence of $N$ items, called an $N$-gram, in which each item is a word, letter, etc. In this paper, we attempt to estimate LRs based on $N$-gram frequency information. A naive estimation approach that uses only $N$-gram frequencies is sensitive to low-frequency (rare) $N$-grams and not applicable to zero-frequency (unobserved) $N$-grams; these are known as the low- and zero-frequency problems, respectively. To address these problems, we propose a method for decomposing $N$-grams into item units and then applying their frequencies along with the original $N$-gram frequencies. Our method can obtain the estimates of unobserved $N$-grams by using the unit frequencies. Although using only unit frequencies ignores dependencies between items, our method takes advantage of the fact that certain items often co-occur in practice and therefore maintains their dependencies by using the relevant $N$-gram frequencies. We also introduce a regularization to achieve robust estimation for rare $N$-grams. Our experimental results demonstrate that our method is effective at solving both problems and can effectively control dependencies.

Unbiased Estimation Equation under $f$-Separable Bregman Distortion Measures

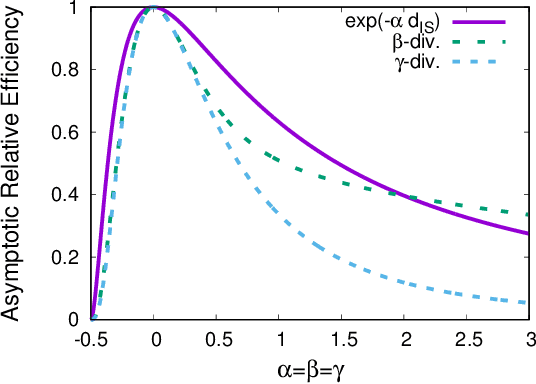
We discuss unbiased estimation equations in a class of objective function using a monotonically increasing function $f$ and Bregman divergence. The choice of the function $f$ gives desirable properties such as robustness against outliers. In order to obtain unbiased estimation equations, analytically intractable integrals are generally required as bias correction terms. In this study, we clarify the combination of Bregman divergence, statistical model, and function $f$ in which the bias correction term vanishes. Focusing on Mahalanobis and Itakura-Saito distances, we provide a generalization of fundamental existing results and characterize a class of distributions of positive reals with a scale parameter, which includes the gamma distribution as a special case. We discuss the possibility of latent bias minimization when the proportion of outliers is large, which is induced by the extinction of the bias correction term.

Multi-Decoder RNN Autoencoder Based on Variational Bayes Method

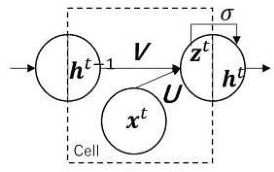
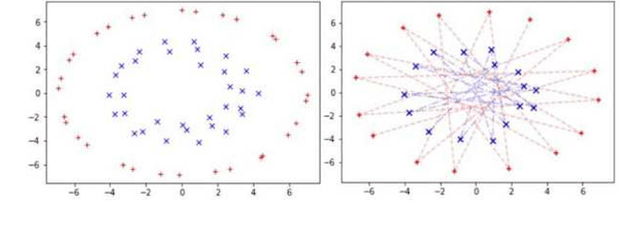
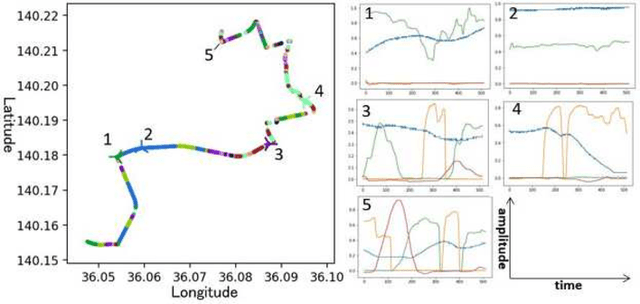
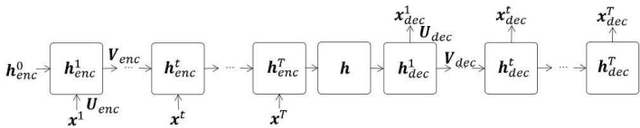
Clustering algorithms have wide applications and play an important role in data analysis fields including time series data analysis. However, in time series analysis, most of the algorithms used signal shape features or the initial value of hidden variable of a neural network. Little has been discussed on the methods based on the generative model of the time series. In this paper, we propose a new clustering algorithm focusing on the generative process of the signal with a recurrent neural network and the variational Bayes method. Our experiments show that the proposed algorithm not only has a robustness against for phase shift, amplitude and signal length variations but also provide a flexible clustering based on the property of the variational Bayes method.

Generalized Dirichlet-process-means for f-separable distortion measures

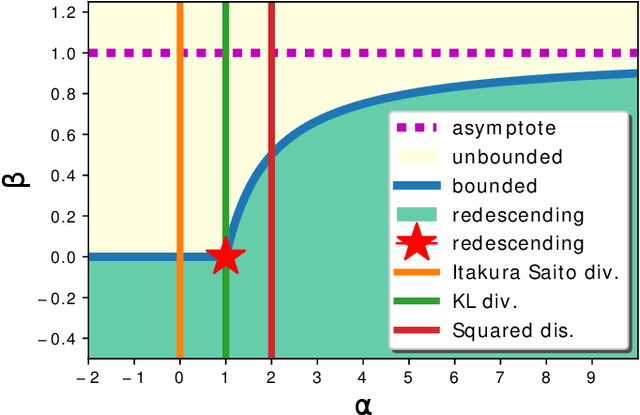
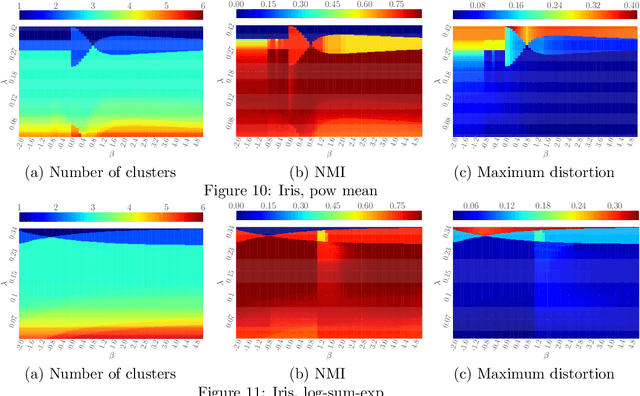
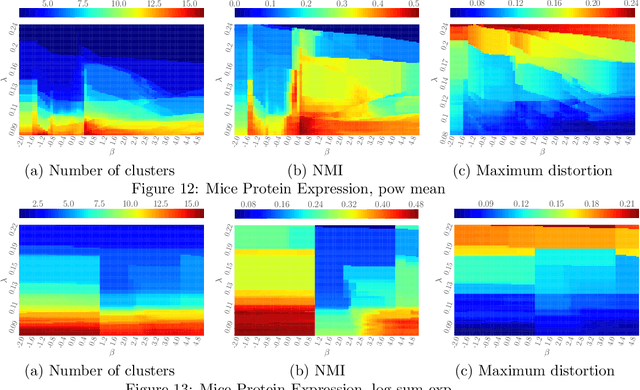
DP-means clustering was obtained as an extension of K-means clustering. While it is implemented with a simple and efficient algorithm, it can estimate the number of clusters simultaneously. However, DP-means is specifically designed for the average distortion measure. Therefore, it is vulnerable to outliers in data, and it can cause large maximum distortion in clusters. In this work, we extend the objective function of the DP-means to f-separable distortion measures and propose a unified learning algorithm to overcome the above problems by the selection of the function f. Furthermore, the influence function of the estimated cluster center is analyzed to evaluate the robustness against outliers. We show the effectiveness of the generalized method by numerical experiments using real datasets.

Bayesian Properties of Normalized Maximum Likelihood and its Fast Computation

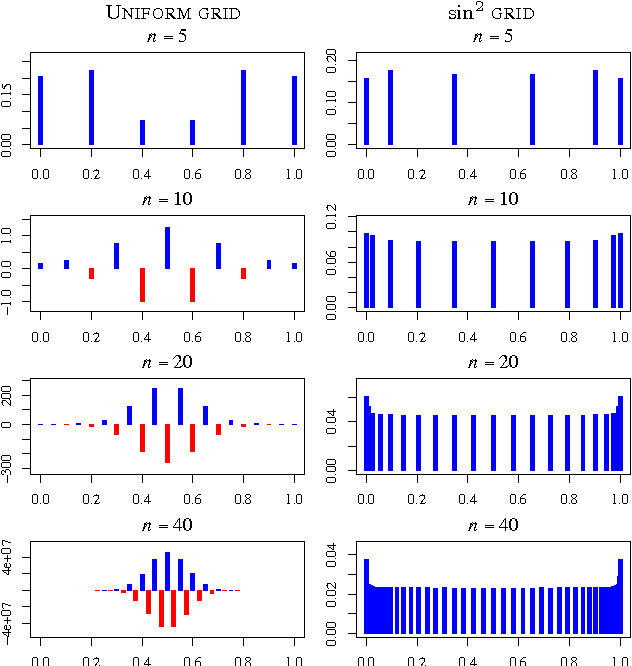
The normalized maximized likelihood (NML) provides the minimax regret solution in universal data compression, gambling, and prediction, and it plays an essential role in the minimum description length (MDL) method of statistical modeling and estimation. Here we show that the normalized maximum likelihood has a Bayes-like representation as a mixture of the component models, even in finite samples, though the weights of linear combination may be both positive and negative. This representation addresses in part the relationship between MDL and Bayes modeling. This representation has the advantage of speeding the calculation of marginals and conditionals required for coding and prediction applications.

Rate-Distortion Bounds for an Epsilon-Insensitive Distortion Measure

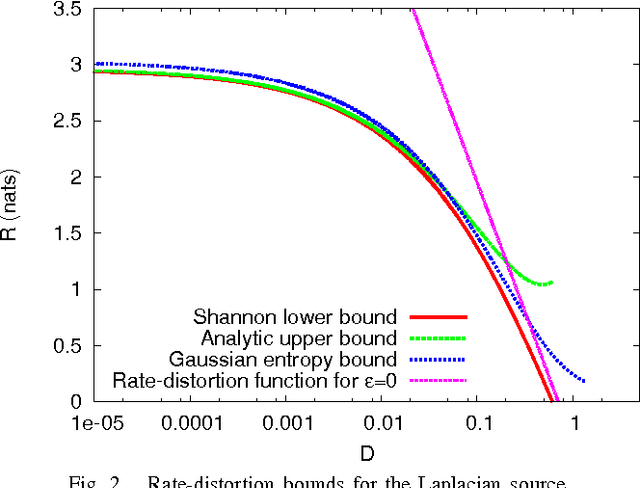
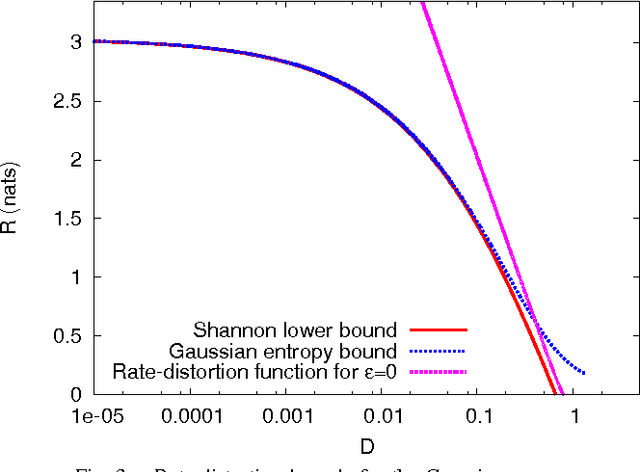
Direct evaluation of the rate-distortion function has rarely been achieved when it is strictly greater than its Shannon lower bound. In this paper, we consider the rate-distortion function for the distortion measure defined by an epsilon-insensitive loss function. We first present the Shannon lower bound applicable to any source distribution with finite differential entropy. Then, focusing on the Laplacian and Gaussian sources, we prove that the rate-distortion functions of these sources are strictly greater than their Shannon lower bounds and obtain analytically evaluable upper bounds for the rate-distortion functions. Small distortion limit and numerical evaluation of the bounds suggest that the Shannon lower bound provides a good approximation to the rate-distortion function for the epsilon-insensitive distortion measure.