Exploring Major Transitions in the Evolution of Biological Cognition With Artificial Neural Networks

Transitional accounts of evolution emphasise a few changes that shape what is evolvable, with dramatic consequences for derived lineages. More recently it has been proposed that cognition might also have evolved via a series of major transitions that manipulate the structure of biological neural networks, fundamentally changing the flow of information. We used idealised models of information flow, artificial neural networks (ANNs), to evaluate whether changes in information flow in a network can yield a transitional change in cognitive performance. We compared networks with feed-forward, recurrent and laminated topologies, and tested their performance learning artificial grammars that differed in complexity, controlling for network size and resources. We documented a qualitative expansion in the types of input that recurrent networks can process compared to feed-forward networks, and a related qualitative increase in performance for learning the most complex grammars. We also noted how the difficulty in training recurrent networks poses a form of transition barrier and contingent irreversibility -- other key features of evolutionary transitions. Not all changes in network topology confer a performance advantage in this task set. Laminated networks did not outperform non-laminated networks in grammar learning. Overall, our findings show how some changes in information flow can yield transitions in cognitive performance.

Proposal of a Score Based Approach to Sampling Using Monte Carlo Estimation of Score and Oracle Access to Target Density

Score based approaches to sampling have shown much success as a generative algorithm to produce new samples from a target density given a pool of initial samples. In this work, we consider if we have no initial samples from the target density, but rather $0^{th}$ and $1^{st}$ order oracle access to the log likelihood. Such problems may arise in Bayesian posterior sampling, or in approximate minimization of non-convex functions. Using this knowledge alone, we propose a Monte Carlo method to estimate the score empirically as a particular expectation of a random variable. Using this estimator, we can then run a discrete version of the backward flow SDE to produce samples from the target density. This approach has the benefit of not relying on a pool of initial samples from the target density, and it does not rely on a neural network or other black box model to estimate the score.

Bayesian Properties of Normalized Maximum Likelihood and its Fast Computation

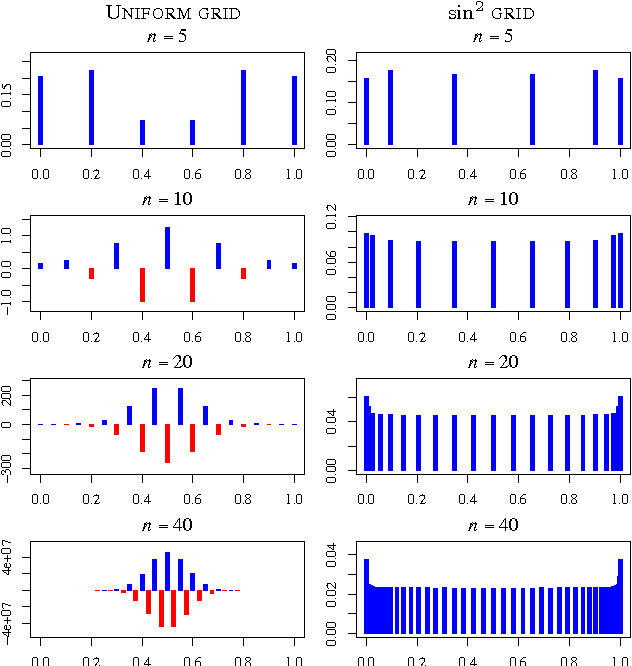
The normalized maximized likelihood (NML) provides the minimax regret solution in universal data compression, gambling, and prediction, and it plays an essential role in the minimum description length (MDL) method of statistical modeling and estimation. Here we show that the normalized maximum likelihood has a Bayes-like representation as a mixture of the component models, even in finite samples, though the weights of linear combination may be both positive and negative. This representation addresses in part the relationship between MDL and Bayes modeling. This representation has the advantage of speeding the calculation of marginals and conditionals required for coding and prediction applications.