Rate-Distortion Bounds for an Epsilon-Insensitive Distortion Measure

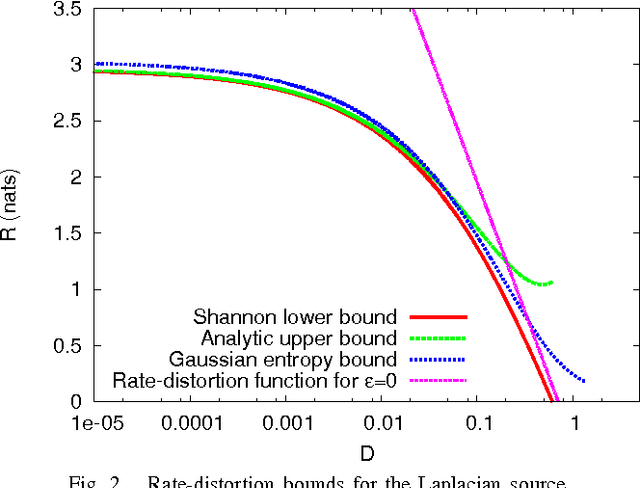
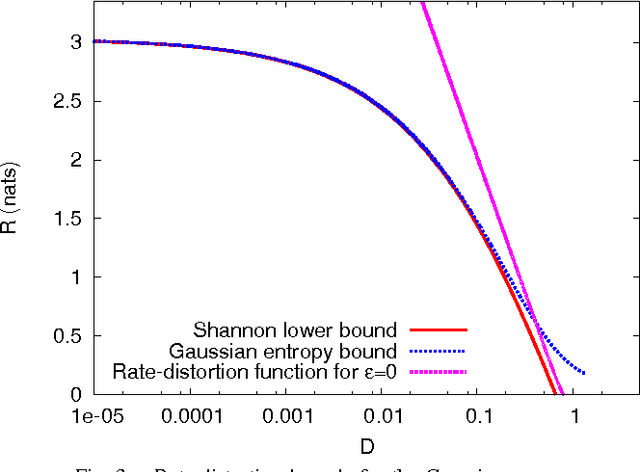
Direct evaluation of the rate-distortion function has rarely been achieved when it is strictly greater than its Shannon lower bound. In this paper, we consider the rate-distortion function for the distortion measure defined by an epsilon-insensitive loss function. We first present the Shannon lower bound applicable to any source distribution with finite differential entropy. Then, focusing on the Laplacian and Gaussian sources, we prove that the rate-distortion functions of these sources are strictly greater than their Shannon lower bounds and obtain analytically evaluable upper bounds for the rate-distortion functions. Small distortion limit and numerical evaluation of the bounds suggest that the Shannon lower bound provides a good approximation to the rate-distortion function for the epsilon-insensitive distortion measure.