Unbiased Estimating Equation on Inverse Divergence and Its Conditions

This paper focuses on the Bregman divergence defined by the reciprocal function, called the inverse divergence. For the loss function defined by the monotonically increasing function $f$ and inverse divergence, the conditions for the statistical model and function $f$ under which the estimating equation is unbiased are clarified. Specifically, we characterize two types of statistical models, an inverse Gaussian type and a mixture of generalized inverse Gaussian type distributions, to show that the conditions for the function $f$ are different for each model. We also define Bregman divergence as a linear sum over the dimensions of the inverse divergence and extend the results to the multi-dimensional case.

Overfitting in quantum machine learning and entangling dropout

The ultimate goal in machine learning is to construct a model function that has a generalization capability for unseen dataset, based on given training dataset. If the model function has too much expressibility power, then it may overfit to the training data and as a result lose the generalization capability. To avoid such overfitting issue, several techniques have been developed in the classical machine learning regime, and the dropout is one such effective method. This paper proposes a straightforward analogue of this technique in the quantum machine learning regime, the entangling dropout, meaning that some entangling gates in a given parametrized quantum circuit are randomly removed during the training process to reduce the expressibility of the circuit. Some simple case studies are given to show that this technique actually suppresses the overfitting.

Unbiased Estimation Equation under $f$-Separable Bregman Distortion Measures

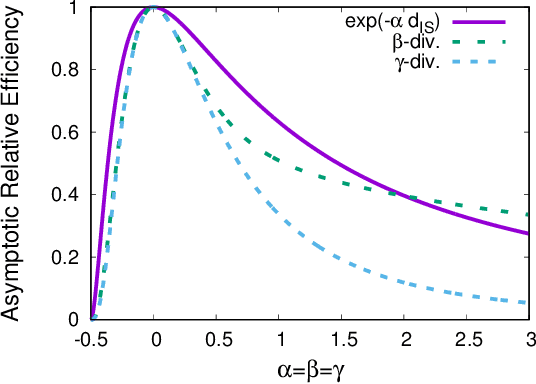
We discuss unbiased estimation equations in a class of objective function using a monotonically increasing function $f$ and Bregman divergence. The choice of the function $f$ gives desirable properties such as robustness against outliers. In order to obtain unbiased estimation equations, analytically intractable integrals are generally required as bias correction terms. In this study, we clarify the combination of Bregman divergence, statistical model, and function $f$ in which the bias correction term vanishes. Focusing on Mahalanobis and Itakura-Saito distances, we provide a generalization of fundamental existing results and characterize a class of distributions of positive reals with a scale parameter, which includes the gamma distribution as a special case. We discuss the possibility of latent bias minimization when the proportion of outliers is large, which is induced by the extinction of the bias correction term.

Multi-Decoder RNN Autoencoder Based on Variational Bayes Method

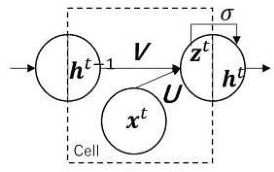
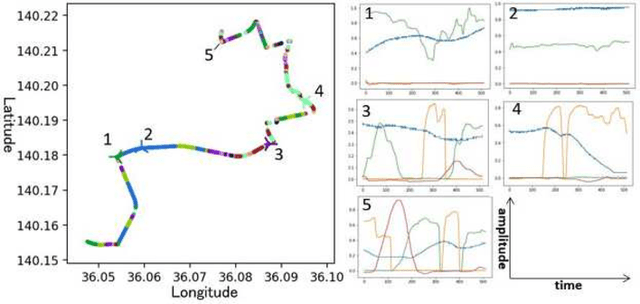
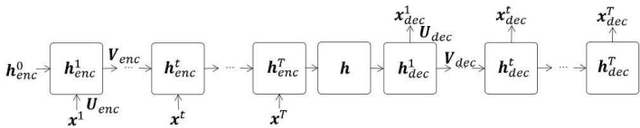
Clustering algorithms have wide applications and play an important role in data analysis fields including time series data analysis. However, in time series analysis, most of the algorithms used signal shape features or the initial value of hidden variable of a neural network. Little has been discussed on the methods based on the generative model of the time series. In this paper, we propose a new clustering algorithm focusing on the generative process of the signal with a recurrent neural network and the variational Bayes method. Our experiments show that the proposed algorithm not only has a robustness against for phase shift, amplitude and signal length variations but also provide a flexible clustering based on the property of the variational Bayes method.

Extendable NFV-Integrated Control Method Using Reinforcement Learning

Network functions virtualization (NFV) enables telecommunications service providers to realize various network services by flexibly combining multiple virtual network functions (VNFs). To provide such services, an NFV control method should optimally allocate such VNFs into physical networks and servers by taking account of the combination(s) of objective functions and constraints for each metric defined for each VNF type, e.g., VNF placements and routes between the VNFs. The NFV control method should also be extendable for adding new metrics or changing the combination of metrics. One approach for NFV control to optimize allocations is to construct an algorithm that simultaneously solves the combined optimization problem. However, this approach is not extendable because the problem needs to be reformulated every time a new metric is added or a combination of metrics is changed. Another approach involves using an extendable network-control architecture that coordinates multiple control algorithms specified for individual metrics. However, to the best of our knowledge, no method has been developed that can optimize allocations through this kind of coordination. In this paper, we propose an extendable NFV-integrated control method by coordinating multiple control algorithms. We also propose an efficient coordination algorithm based on reinforcement learning. Finally, we evaluate the effectiveness of the proposed method through simulations.

Generalized Dirichlet-process-means for f-separable distortion measures

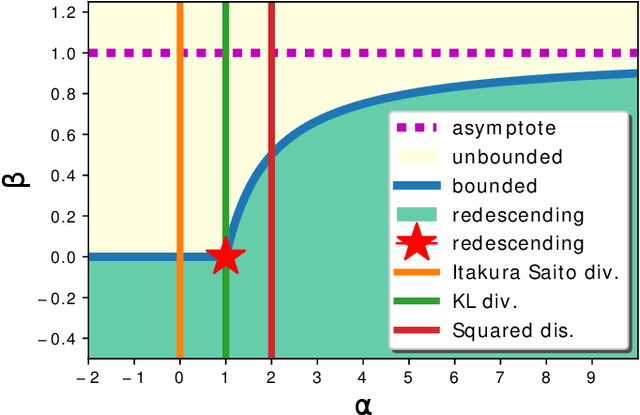
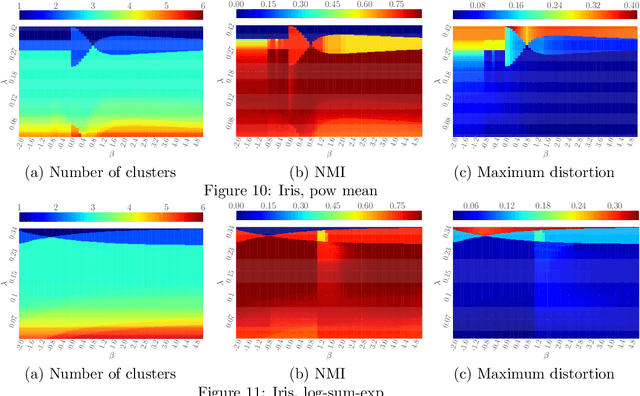
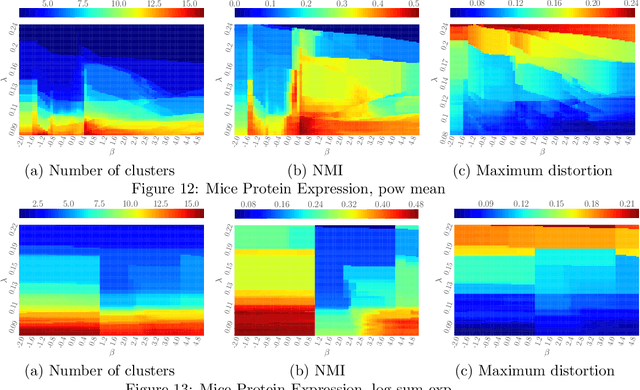
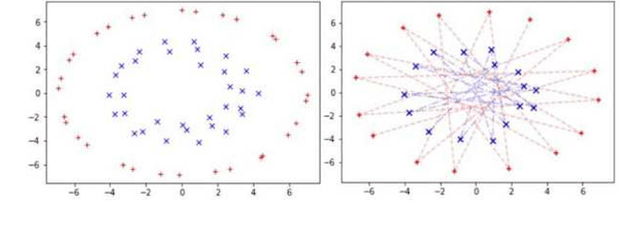
DP-means clustering was obtained as an extension of K-means clustering. While it is implemented with a simple and efficient algorithm, it can estimate the number of clusters simultaneously. However, DP-means is specifically designed for the average distortion measure. Therefore, it is vulnerable to outliers in data, and it can cause large maximum distortion in clusters. In this work, we extend the objective function of the DP-means to f-separable distortion measures and propose a unified learning algorithm to overcome the above problems by the selection of the function f. Furthermore, the influence function of the estimated cluster center is analyzed to evaluate the robustness against outliers. We show the effectiveness of the generalized method by numerical experiments using real datasets.