Breaking the curse of dimensionality with Isolation Kernel

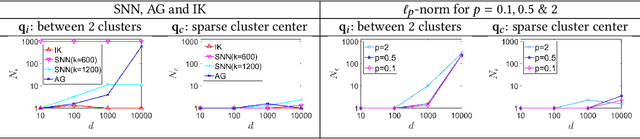
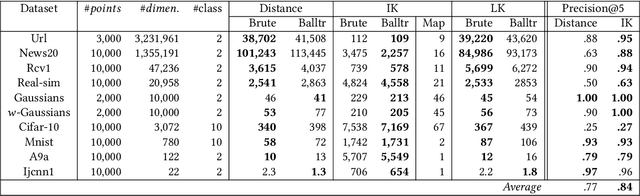
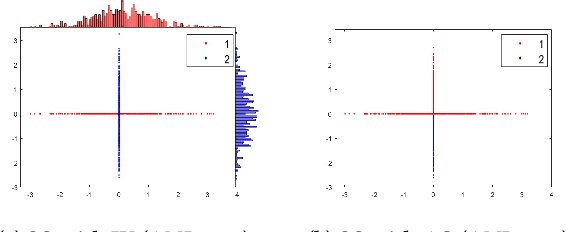
The curse of dimensionality has been studied in different aspects. However, breaking the curse has been elusive. We show for the first time that it is possible to break the curse using the recently introduced Isolation Kernel. We show that only Isolation Kernel performs consistently well in indexed search, spectral & density peaks clustering, SVM classification and t-SNE visualization in both low and high dimensions, compared with distance, Gaussian and linear kernels. This is also supported by our theoretical analyses that Isolation Kernel is the only kernel that has the provable ability to break the curse, compared with existing metric-based Lipschitz continuous kernels.

Isolation Distributional Kernel: A New Tool for Point & Group Anomaly Detection

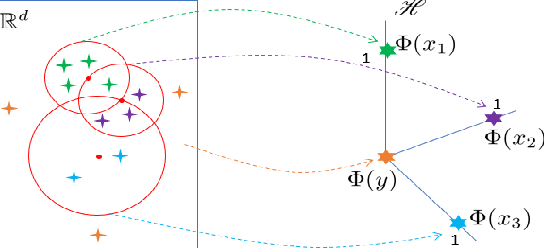
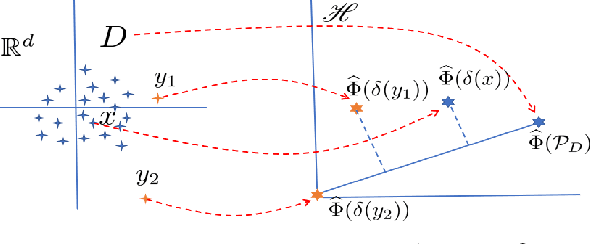
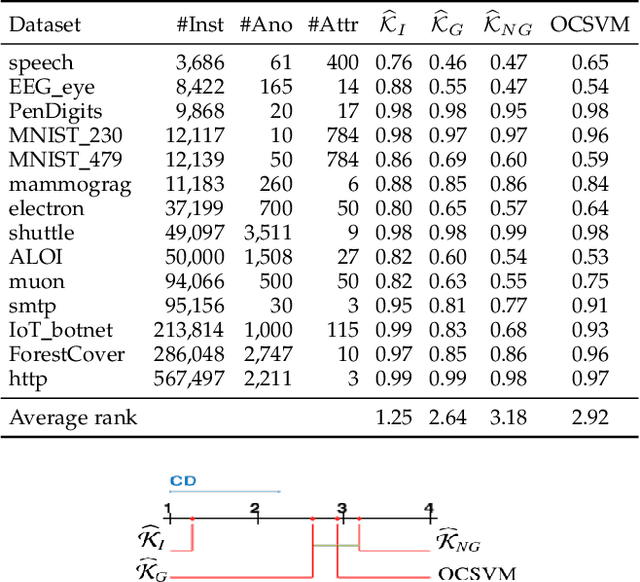
We introduce Isolation Distributional Kernel as a new way to measure the similarity between two distributions. Existing approaches based on kernel mean embedding, which convert a point kernel to a distributional kernel, have two key issues: the point kernel employed has a feature map with intractable dimensionality; and it is {\em data independent}. This paper shows that Isolation Distributional Kernel (IDK), which is based on a {\em data dependent} point kernel, addresses both key issues. We demonstrate IDK's efficacy and efficiency as a new tool for kernel based anomaly detection for both point and group anomalies. Without explicit learning, using IDK alone outperforms existing kernel based point anomaly detector OCSVM and other kernel mean embedding methods that rely on Gaussian kernel. For group anomaly detection,we introduce an IDK based detector called IDK$^2$. It reformulates the problem of group anomaly detection in input space into the problem of point anomaly detection in Hilbert space, without the need for learning. IDK$^2$ runs orders of magnitude faster than group anomaly detector OCSMM.We reveal for the first time that an effective kernel based anomaly detector based on kernel mean embedding must employ a characteristic kernel which is data dependent.

Isolation Kernel: The X Factor in Efficient and Effective Large Scale Online Kernel Learning

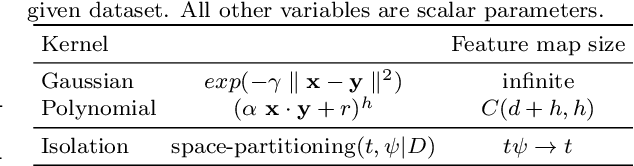
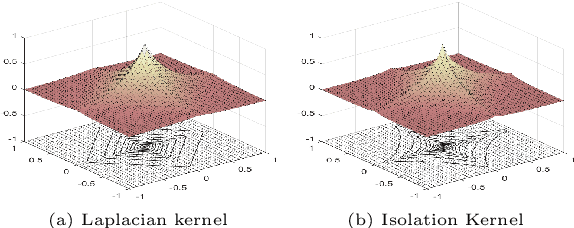
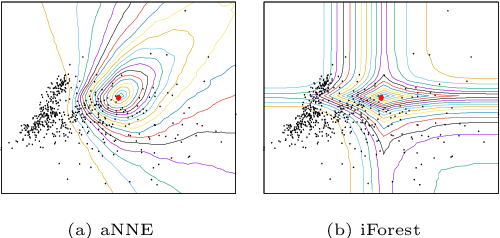
Large scale online kernel learning aims to build an efficient and scalable kernel-based predictive model incrementally from a sequence of potentially infinite data points. To achieve this aim, the method must be able to deal with a potentially infinite number of support vectors. The current state-of-the-art is unable to deal with even a moderate number of support vectors. This paper identifies the root cause of the current methods, i.e., the type of kernel used which has a feature map of infinite dimensionality. With this revelation and together with our discovery that a recently introduced Isolation Kernel has a finite feature map, to achieve the above aim of large scale online kernel learning becomes extremely simple---simply use Isolation Kernel instead of kernels having infinite feature map. We show for the first time that online kernel learning is able to deal with a potentially infinite number of support vectors.

Learning Graph Representation via Formal Concept Analysis

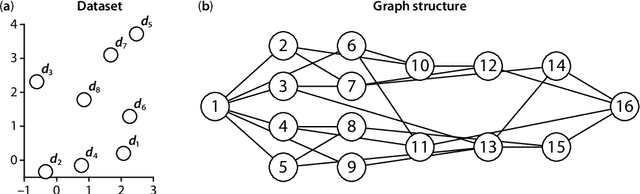
We present a novel method that can learn a graph representation from multivariate data. In our representation, each node represents a cluster of data points and each edge represents the subset-superset relationship between clusters, which can be mutually overlapped. The key to our method is to use formal concept analysis (FCA), which can extract hierarchical relationships between clusters based on the algebraic closedness property. We empirically show that our method can effectively extract hierarchical structures of clusters compared to the baseline method.

Analysis of Cause-Effect Inference via Regression Errors

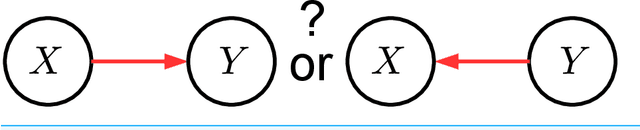
We address the problem of inferring the causal relation between two variables by comparing the least-squares errors of the predictions in both possible causal directions. Under the assumption of an independence between the function relating cause and effect, the conditional noise distribution, and the distribution of the cause, we show that the errors are smaller in causal direction if both variables are equally scaled and the causal relation is close to deterministic. Based on this, we provide an easily applicable algorithm that only requires a regression in both possible causal directions and a comparison of the errors. The performance of the algorithm is compared with different related causal inference methods in various artificial and real-world data sets.

Error Asymmetry in Causal and Anticausal Regression

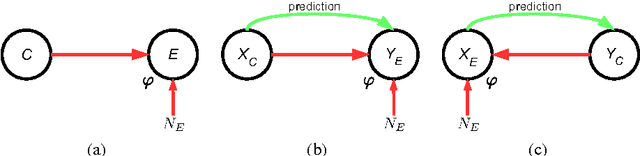
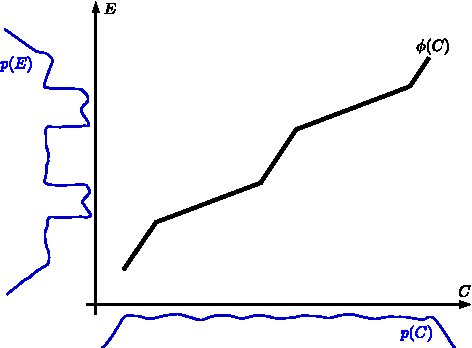
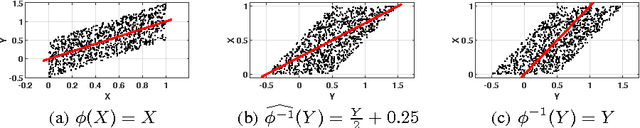
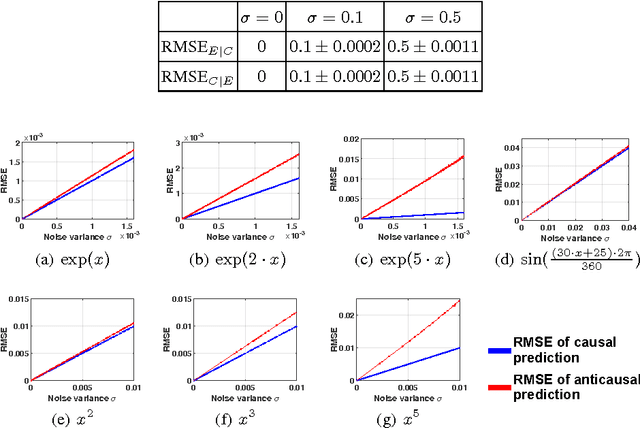
It is generally difficult to make any statements about the expected prediction error in an univariate setting without further knowledge about how the data were generated. Recent work showed that knowledge about the real underlying causal structure of a data generation process has implications for various machine learning settings. Assuming an additive noise and an independence between data generating mechanism and its input, we draw a novel connection between the intrinsic causal relationship of two variables and the expected prediction error. We formulate the theorem that the expected error of the true data generating function as prediction model is generally smaller when the effect is predicted from its cause and, on the contrary, greater when the cause is predicted from its effect. The theorem implies an asymmetry in the error depending on the prediction direction. This is further corroborated with empirical evaluations in artificial and real-world data sets.

A Bayesian estimation approach to analyze non-Gaussian data-generating processes with latent classes

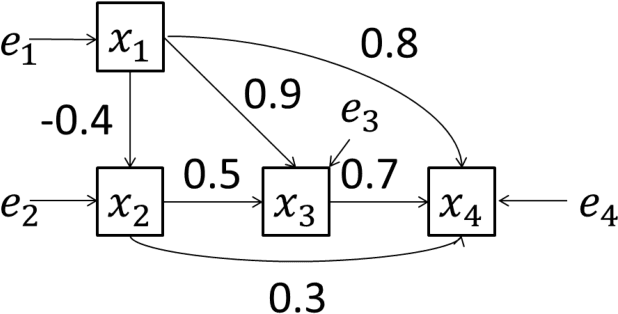
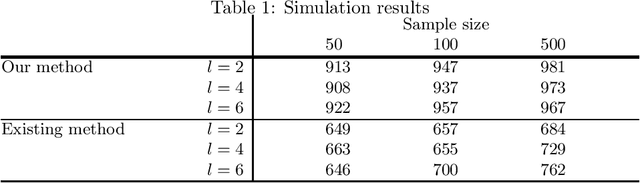
A large amount of observational data has been accumulated in various fields in recent times, and there is a growing need to estimate the generating processes of these data. A linear non-Gaussian acyclic model (LiNGAM) based on the non-Gaussianity of external influences has been proposed to estimate the data-generating processes of variables. However, the results of the estimation can be biased if there are latent classes. In this paper, we first review LiNGAM, its extended model, as well as the estimation procedure for LiNGAM in a Bayesian framework. We then propose a new Bayesian estimation procedure that solves the problem.

Causal Discovery in a Binary Exclusive-or Skew Acyclic Model: BExSAM

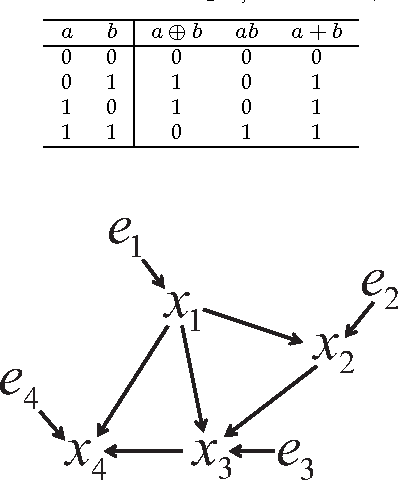
Discovering causal relations among observed variables in a given data set is a major objective in studies of statistics and artificial intelligence. Recently, some techniques to discover a unique causal model have been explored based on non-Gaussianity of the observed data distribution. However, most of these are limited to continuous data. In this paper, we present a novel causal model for binary data and propose an efficient new approach to deriving the unique causal model governing a given binary data set under skew distributions of external binary noises. Experimental evaluation shows excellent performance for both artificial and real world data sets.

Identifiability of an Integer Modular Acyclic Additive Noise Model and its Causal Structure Discovery

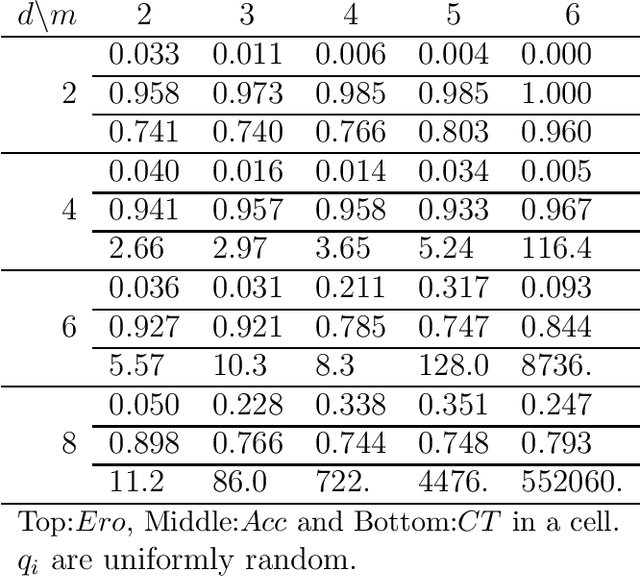
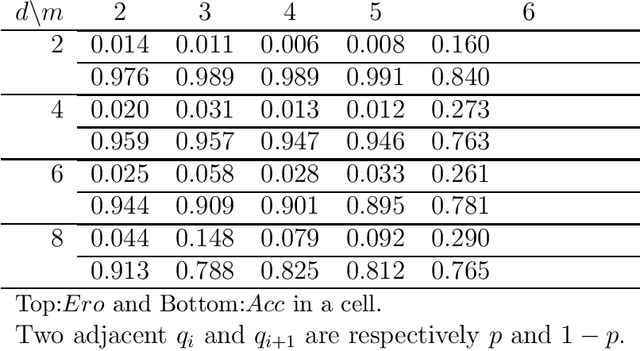
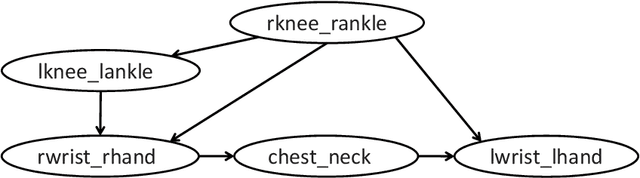
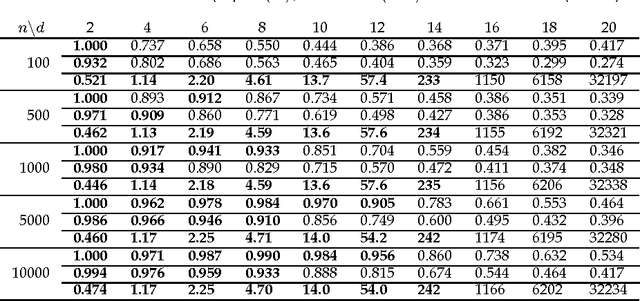
The notion of causality is used in many situations dealing with uncertainty. We consider the problem whether causality can be identified given data set generated by discrete random variables rather than continuous ones. In particular, for non-binary data, thus far it was only known that causality can be identified except rare cases. In this paper, we present necessary and sufficient condition for an integer modular acyclic additive noise (IMAN) of two variables. In addition, we relate bivariate and multivariate causal identifiability in a more explicit manner, and develop a practical algorithm to find the order of variables and their parent sets. We demonstrate its performance in applications to artificial data and real world body motion data with comparisons to conventional methods.

Anomaly detection in reconstructed quantum states using a machine-learning technique

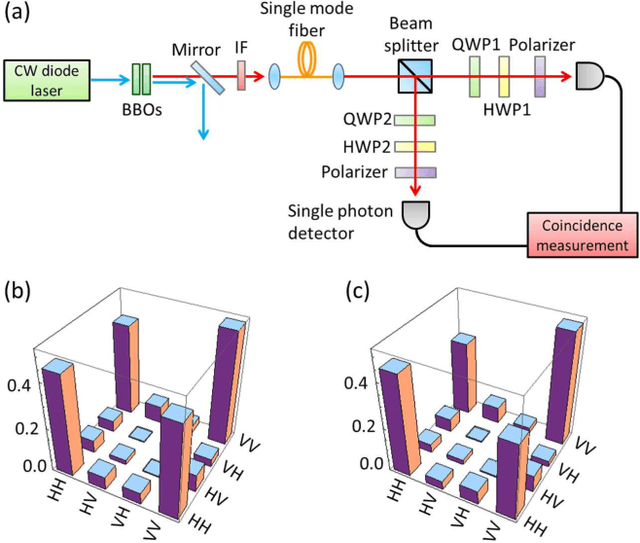
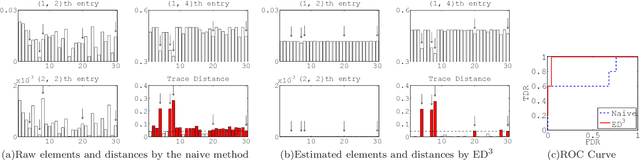
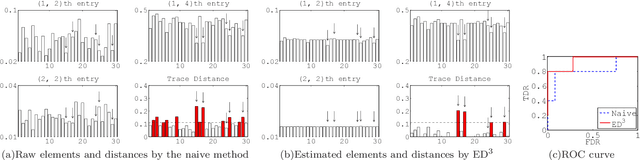
The accurate detection of small deviations in given density matrices is important for quantum information processing. Here we propose a new method based on the concept of data mining. We demonstrate that the proposed method can more accurately detect small erroneous deviations in reconstructed density matrices, which contain intrinsic fluctuations due to the limited number of samples, than a naive method of checking the trace distance from the average of the given density matrices. This method has the potential to be a key tool in broad areas of physics where the detection of small deviations of quantum states reconstructed using a limited number of samples are essential.