Isolation Distributional Kernel: A New Tool for Point & Group Anomaly Detection
Paper and Code
Sep 24, 2020
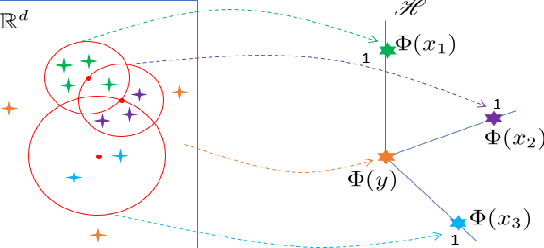
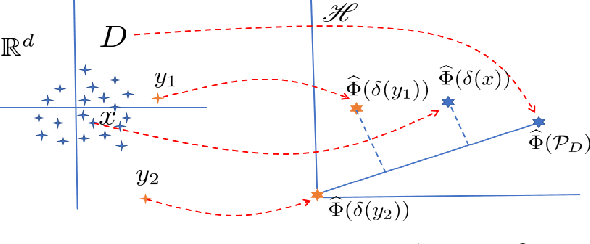
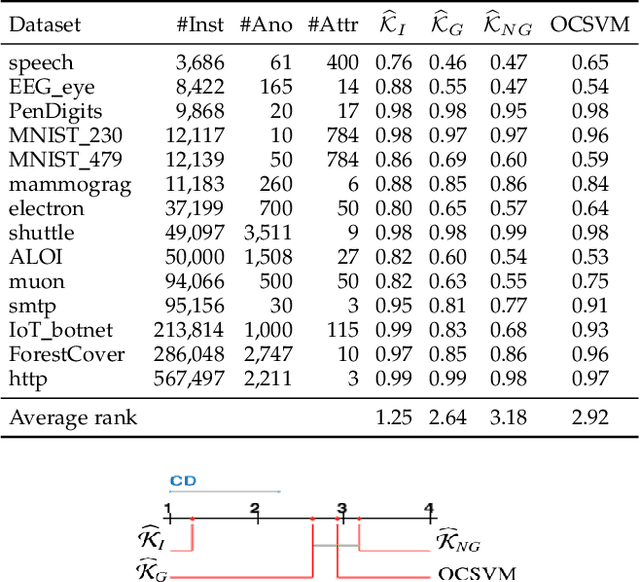
We introduce Isolation Distributional Kernel as a new way to measure the similarity between two distributions. Existing approaches based on kernel mean embedding, which convert a point kernel to a distributional kernel, have two key issues: the point kernel employed has a feature map with intractable dimensionality; and it is {\em data independent}. This paper shows that Isolation Distributional Kernel (IDK), which is based on a {\em data dependent} point kernel, addresses both key issues. We demonstrate IDK's efficacy and efficiency as a new tool for kernel based anomaly detection for both point and group anomalies. Without explicit learning, using IDK alone outperforms existing kernel based point anomaly detector OCSVM and other kernel mean embedding methods that rely on Gaussian kernel. For group anomaly detection,we introduce an IDK based detector called IDK$^2$. It reformulates the problem of group anomaly detection in input space into the problem of point anomaly detection in Hilbert space, without the need for learning. IDK$^2$ runs orders of magnitude faster than group anomaly detector OCSMM.We reveal for the first time that an effective kernel based anomaly detector based on kernel mean embedding must employ a characteristic kernel which is data dependent.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge