Takafumi Ono
Consistent Nonparametric Different-Feature Selection via the Sparsest $k$-Subgraph Problem
Aug 01, 2017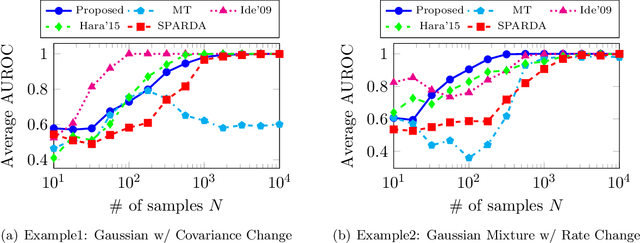

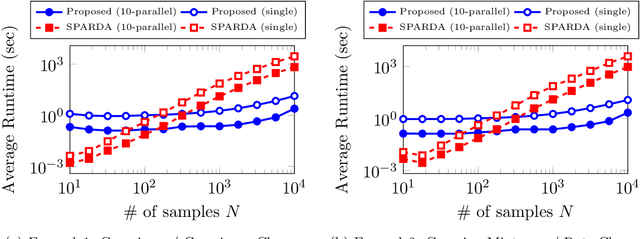
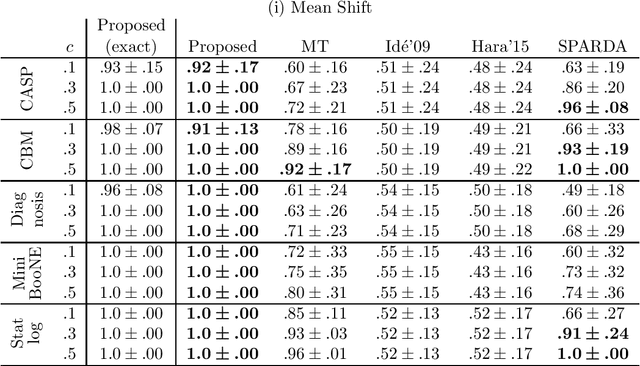
Abstract:Two-sample feature selection is the problem of finding features that describe a difference between two probability distributions, which is a ubiquitous problem in both scientific and engineering studies. However, existing methods have limited applicability because of their restrictive assumptions on data distributoins or computational difficulty. In this paper, we resolve these difficulties by formulating the problem as a sparsest $k$-subgraph problem. The proposed method is nonparametric and does not assume any specific parametric models on the data distributions. We show that the proposed method is computationally efficient and does not require any extra computation for model selection. Moreover, we prove that the proposed method provides a consistent estimator of features under mild conditions. Our experimental results show that the proposed method outperforms the current method with regard to both accuracy and computation time.
Anomaly detection in reconstructed quantum states using a machine-learning technique
Jan 20, 2014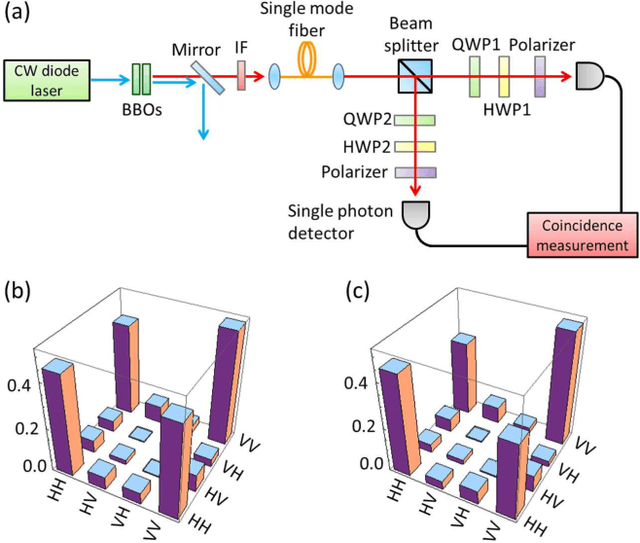
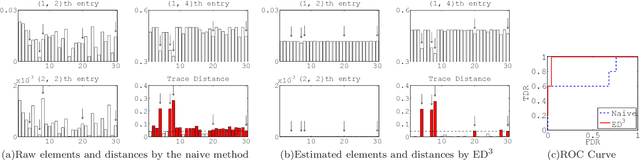

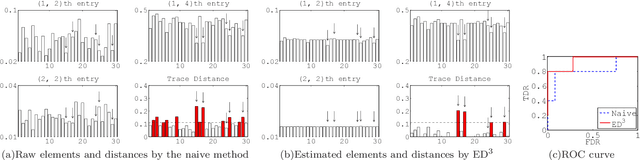
Abstract:The accurate detection of small deviations in given density matrices is important for quantum information processing. Here we propose a new method based on the concept of data mining. We demonstrate that the proposed method can more accurately detect small erroneous deviations in reconstructed density matrices, which contain intrinsic fluctuations due to the limited number of samples, than a naive method of checking the trace distance from the average of the given density matrices. This method has the potential to be a key tool in broad areas of physics where the detection of small deviations of quantum states reconstructed using a limited number of samples are essential.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge